Шифр подстановки
Шифр подстано́вки — это метод шифрования, в котором элементы исходного открытого текста заменяются зашифрованным текстом в соответствии с некоторым правилом. Элементами текста могут быть отдельные символы (самый распространённый случай), пары букв, тройки букв, комбинирование этих случаев и так далее. В классической криптографии различают четыре типа шифра подстановки[1]:
- Одноалфавитный шифр подстановки (например, шифр простой замены, шифр Цезаря) — шифр, при котором каждый символ открытого текста заменяется на некоторый, фиксированный при данном ключе символ того же алфавита.
- Однозвучный шифр подстановки (например, книжный шифр) похож на одноалфавитный, за исключением того, что символ открытого текста может быть заменён одним из нескольких возможных символов.
- Полиграммный шифр подстановки заменяет не один символ, а целую группу. Пример: шифр Плейфера.
- Полиалфавитный шифр подстановки состоит из нескольких шифров простой замены. Примеры: шифр Виженера, шифр Бофора, одноразовый блокнот.
В качестве альтернативы шифрам подстановки можно рассматривать перестановочные шифры. В них, элементы текста переставляются в ином от исходного порядке, а сами элементы остаются неизменными. Напротив, в шифрах подстановки, элементы текста не меняют свою последовательность, а изменяются сами.
История[править | править код]
Использование шифров подстановки берет свое начало в Месопотамии. С целью сокрытия информации о рецепте производства глазури для гончарных изделий автор заменял часть слов на цифры и клинописные знаки. Римский император Гай Юлий Цезарь при написании секретных сообщений смещал каждую букву алфавита на 3 позиции. Данный вид шифров подстановки впоследствии назвали его именем, шифр Цезаря. Другой не менее известный шифр античности, Атбаш, применялся в Библии для создания скрытых посланий. Каждая буква слова заменялась её зеркальным отражением в алфавите[2] [3].

Одним из первых шифровальных устройств принято считать линейку Энея, при использовании которой длинная нить продевалась через прорезь, а затем через проделанные в линейке отверстия. Рядом с отверстиями располагались соответствующие им буквы. На нити завязывался узелок в месте прохождения её через отверстие. Таким образом осуществлялась замена текста послания на последовательность расстояний между узелками. Данное устройство было изобретено древнегреческим полководцем Энеем Тактиком в IV веке до н. э.[4][5]
С началом использования частотного анализа для вскрытия моноалфавитных шифров в IX веке, появилась необходимость в изменении частотности появления символов обычного текста. С этой целью стал применяться однозвучный шифр подстановки, сутью которого было сопоставление нескольких заменяющих символов одной букве пропорционально частотности появление этой буквы в различных текстах. Секретарь антипапы Клемёнтия VII Габриель де Лавинда в XV веке впервые использует омофоны для обеспечения приблизительно одинаковой частотности гласных букв. Спустя 65 лет Леон Баттиста Альберти подробно описывает однозвучный шифр подстановки в своей книге «Трактат о шифрах». Основной проблемой распространения омофонической замены была необходимость использования расширенного алфавита для зашифровки сообщений.[6][7] [8][9]
Этого недостатка были лишены полиалфавитные шифры, первый из которых был описан немецким монахом Иоганном Тритемием. Согласно методу, описанному в его трактате «Полиграфия» очередная буква заменялась символом из собственного шифралфавита, при этом каждый следующий алфавит получался из предыдущего с помощью сдвига на одну букву. Особенную популярность получил полиалфавитный шифр, описанный Блезом де Виженером в 1585 году. В качестве ключа к шифру использовалось произвольное слово. Соответствующий данному слову набор шифралфавитов определялся из таблицы Виженера.[10]
В 1854 году английским физиком Чарльзом Уитстоном публикуется полиграммный шифр, впоследствии названный именем лорда Лайона Плейфера. Данный шифр осуществляет замену пар букв (биграмм) на одиночные символы, что значительно увеличивает его криптостойкость к частотному анализу.[11]
С появлением ЭВМ полиалфавитные и полиграммные шифры отошли на второй план, а на смену им пришли новые более надежные блочные шифры.[12]
Шифры простой замены[править | править код]
В шифрах простой замены замена производится только над одним-единственным символом. Для наглядной демонстрации шифра простой замены достаточно выписать под заданным алфавитом тот же алфавит, но в другом порядке или, например, со смещением. Записанный таким образом алфавит называют алфавитом замены.
Примеры шифров простой замены[править | править код]
Атбаш[править | править код]
Шифр простой замены, использованный для еврейского алфавита и получивший оттуда своё название. Шифрование происходит заменой первой буквы алфавита на последнюю, второй на предпоследнюю (алеф (первая буква) заменяется на тав (последнюю), бет (вторая) заменяется на шин (предпоследняя); из этих сочетаний шифр и получил своё название).[13] Шифр Атбаш для английского алфавита:
| Исходный алфавит: | A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
| Алфавит замены: | Z Y X W V U T S R Q P O N M L K J I H G F E D C B A |
Шифр Цезаря[править | править код]
Шифр Цезаря — один из древнейших шифров. При шифровании каждая буква заменяется другой, отстоящей от нее в алфавите на фиксированное число позиций. Шифр назван в честь римского императора Гая Юлия Цезаря, использовавшего его для секретной переписки. Естественным развитием шифра Цезаря стал шифр Виженера. Шифрование с использованием ключа :
| Исходный алфавит: | A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
| Алфавит замены: | E F G H I J K L M N O P Q R S T U V W X Y Z A B C D |
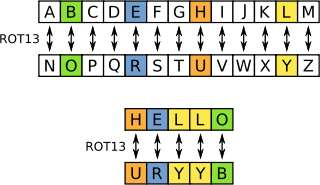
Современным примером шифра Цезаря является ROT13. Он сдвигает каждый символ английского алфавита на 13 позиций. Используется в интернет-форумах, как средство для сокрытия спойлеров, основных мыслей, решений загадок и оскорбительных материалов от случайного взгляда.[14]
Шифр с использованием кодового слова[править | править код]
Шифр с использованием кодового слова является одним из самых простых как в реализации, так и в расшифровывании. Идея заключается в том, что выбирается кодовое слово, которое пишется впереди, затем выписываются остальные буквы алфавита в своем порядке. Шифр с использованием кодового слова WORD.
| Исходный алфавит: | A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
| Алфавит замены: | W O R D A B C E F G H I J K L M N P Q S T U V X Y Z |
Как мы видим, при использовании короткого кодового слова мы получаем очень и очень простую замену. Мы можем использовать слово с повторяющимися буквами в качестве кодового слова, но только в том случае, если уберём из кодового слова лишние буквы, иначе это приведёт к неоднозначности расшифровки, то есть двум различным буквам исходного алфавита будет соответствовать одна и та же буква шифрованного текста.[15]
Метод записи зашифрованных текстов[править | править код]
По традиции, зашифрованный текст пишут блоками (другое название «группы») по 5 символов, не учитывая пунктуацию и пробелы. Это помогает избежать ошибок при передаче шифрованного сообщения и позволяет скрыть границы слов в исходном тексте. Блок содержит 6 символов, так как раньше их было удобно передавать по телеграфу.
Безопасность шифров простой замены[править | править код]
Главный недостаток этого метода шифрования — это то, что последние буквы алфавита (которые имеют низкие коэффициенты при частотном анализе) имеют тенденцию оставаться в конце. Более защищённый способ построить алфавит замены состоит в том, чтобы выполнить колоночное перемещение (перемещение столбцов) в алфавите, используя ключевое слово, но это нечасто делается.
Несмотря на то, что число возможных ключей является очень большим (26! = 288.4), этот вид шифра может быть легко взломанным. При условии, что сообщение имеет достаточную длину (см. ниже), криптоаналитик может предположить значения некоторых самых распространённых букв исходя из анализа частотного распределения символов в зашифрованном тексте. Это позволяет формировать отдельные слова, которые могут быть предварительно использованы, для последующего получения более полного решения (см. частотный анализ). Согласно расстоянию уникальности английского языка 27.6 букв от зашифрованного текста должно быть достаточно, чтобы взломать шифр простой замены. На практике обычно достаточно около 50 символов для взлома, хотя некоторые шифротексты могут быть взломаны и с меньшим количеством символов, если найдены какие-либо нестандартные структуры. Но при равномерном распределении символов в тексте могут потребоваться куда более длинные шифротексты для взлома.
- расстояние уникальности — термин, используемый в криптографии, обращающейся к длине оригинального шифротекста, которого должно быть достаточно для взлома шифра.[16]
Омофоническая замена[править | править код]
Ранние попытки увеличить сложность частотного анализа шифротекстов состояли в том, чтобы замаскировать реальные частотности символов обычного текста с помощью омофонии. В этих шифрах буквы исходного алфавита соответствуют более чем одному символу из алфавита замены. Обычно символам исходного текста с наивысшей частотностью дают большее количество эквивалентов, чем более редким символам. Таким образом, распределение частотностей становится более равномерным, сильно затрудняя частотный анализ[17].
С тех пор, как для алфавита замены стало требоваться больше чем 26 символов, появилась необходимость в расширенных алфавитах. Одним из самых простых решений является замена алфавита на цифры. Другой метод состоит из простых изменений существующего алфавита: прописные буквы, строчные буквы, перевернутые символы и т. д. Более художественными, хотя не обязательно более надежными, будут омофонические шифры, которые используют полностью изобретённые (вымышленные) алфавиты (как например, шифр в книге «Золотой жук» Э. По, или «Рукопись Войнича». Впрочем, эти шифры не являются примерами омофонической замены).
Примеры омофонических шифров[править | править код]
Номенклатор[править | править код]
Шифр, изданный средневековым чиновником, представляющий собой маленькую книгу с большими омофоническими таблицами замены. Первоначально шифр был ограничен именами важных людей того времени, отсюда и последовало название шифра; в более поздних изданиях этот шифр дополнился большим количеством распространённых слов и географических названий. На основе этого «номенклатора» был составлен Великий Шифр Россиньоля, использовавшийся королём Франции Людовиком XIV. И действительно, после того как этот шифр перестал использоваться, французские архивы были закрытыми ещё в течение нескольких сотен лет.
«Номенклаторы» были стандартом для дипломатической корреспонденции, шпионских сообщений и являлись основным средством антиполитической конспирации с начала XV до конца XVIII века. Хотя правительственные криптоаналитики систематически взламывали «номенклаторы» к середине шестнадцатого столетия. Обычным выходом из этой ситуации было увеличение объёмов таблиц. Но к концу восемнадцатого столетия, когда система начала выходить из употребления, некоторые «номенклаторы» имели до 50 000 символов. Однако не все «номенклаторы» были сломаны.
Великий Шифр Россиньоля[править | править код]
Антуан Россиньоль и его сын Бонавентур Россиньоль изобрели Великий Шифр, который использовал 587 различных чисел.[18] Шифр был настолько силен, что в течение многих столетий никто не мог взломать его, пока это не сделал офицер французской армии, криптограф Этьен Базери в 1893 году на примере одного письма военного министра Лувуа королю Людовику XIV. Он понял, что каждое число кодировало не одну букву, а целый слог. Базери предположил, что последовательность 124-22-125-46-345 кодирует слово «les ennemis» (враги), и, отталкиваясь от этой информации, смог расшифровать весь текст.
Книжный шифр[править | править код]
Книжный шифр — шифр, в котором ключом является книга или небольшая часть текста. Основным требованием будет, чтобы оба корреспондента не только имели одну и ту же книгу, но и те же издание и выпуск. Традиционно книжные шифры работают на основе замены слов в исходном тексте на местоположение этих же слов в книге. Это будет работать до тех пор, пока не встретится слово, которого не будет в книге, тогда сообщение не может быть закодировано.[19] Альтернативный подход, который обходит эту проблему, состоит в том, чтобы заменять отдельные символы, а не слова. Однако такой способ имеет побочный эффект: зашифрованный текст становится очень большого размера (обычно используется от 4 до 6 цифр для шифрования каждого символа или слога).
Полиалфавитные шифры[править | править код]
Дальнейшим продолжением шифров простой замены является многоалфавитные шифры. Абу Аль-Кинди в своих работах показал, что обычные моноалфавитные шифры довольно-таки просто поддаются частотному криптоанализу и первым предложил использовать многоалфавитные шифры. В Европе такие шифры были впервые описаны в 1467 году итальянским архитектором Леон Баттиста Альберти. В XVI веке немецкий аббат Иоганн Тритемий в своей книге «Стенография» представил схему полиалфавитного шифрования в виде таблицы. Более сложный вариант с использованием смешанных алфавитов был описан в 1563 году Джамбаттиста делла Порта в его книге «De Furtivis Literarum Notis» (лат. «Про скрытую значимость отдельных букв»). Суть полиалфавитных шифров заключена в многократном применении различных шифров простой замены к определённому числу букв шифруемого текста. То есть к каждой букве по отдельности применяется один из шифров простой замены.
Примеры полиалфавитных шифров[править | править код]
Шифр Виженера[править | править код]

Шифр Виженера состоит из последовательности нескольких шифров Цезаря с различными значениями сдвига. Для зашифровывания может использоваться таблица алфавитов, называемая tabula recta или квадрат (таблица) Виженера. Применительно к латинскому алфавиту таблица Виженера составляется из строк по 26 символов, причём каждая следующая строка сдвигается на несколько позиций. Таким образом, в таблице получается 26 различных шифров Цезаря. На разных этапах кодировки шифр Виженера использует различные алфавиты из этой таблицы. На каждом этапе шифрования используются различные алфавиты, выбираемые в зависимости от символа ключевого слова.[20] Например, если ключевое слово «CAT», то первая буква открытого текста шифруется с использованием алфавита "C’, вторая «A», третья «T», четвёртая снова «C» и так далее.
Одноразовый блокнот[править | править код]
Этот тип шифра подстановки довольно специфический. Он был изобретен в конце первой мировой войны Гилбертом Вернамом. Клод Шеннон математически доказал его абсолютную криптографическую стойкость в своей работе 1945 года. Для создания шифротекста открытый текст объединяется операцией «исключающее ИЛИ» с ключом (называемым одноразовым блокнотом или шифроблокнотом). При этом использование одноразового блокнота, в большинстве случаев, нецелесообразно, так как требуется, чтобы ключ был такого же размера, что и открытый текст. Также требуется, чтобы ключ был абсолютно случайным, применялся только один раз и хранился в секрете от всех, кроме получателя и отправителя. В связи с этим коммерческое применение шифра Вернама не так распространено в отличие от схем с открытым ключом и он используется, в основном, для передачи сообщений особой важности государственными структурами.[21]
Полиграммные шифры[править | править код]
В полиграммных шифрах подстановки буквы открытого текста заменяются не по одной, а группами. Первое преимущество такого способа заключается в том, что распределение частотностей групп букв значительно более равномерное чем отдельных символов. Во-вторых, для продуктивного частотного анализа требуется больший размер зашифрованного текста, так число различных групп букв значительно больше, чем просто алфавит.
Примеры полиграммных шифров[править | править код]
Шифр Плейфера[править | править код]
Шифр Плейфера — ручная симметричная техника шифрования, в которой впервые использована замена биграмм. Изобретена в 1854 году Чарльзом Уитстоном, но названа именем Лорда Лайона Плейфера, который внедрил данный шифр в государственные службы Великобритании. Шифр предусматривает шифрование пар символов (биграмм) вместо одиночных символов, как в шифре подстановки и в более сложных системах шифрования Виженера.[22][23] Шифр Плейфера использует матрицу 5х5 (для латинского алфавита, для кириллического алфавита необходимо увеличить размер матрицы до 4х8), ячейки которой заполнены смешанным алфавитом (в английских текстах обычно опускается символ «Q», чтобы уменьшить алфавит, в других версиях «I» и «J» объединяются в одну ячейку). Замена затем осуществляется путём представления биграмм, как два угла прямоугольника. Два другие угла в диаграмме используются для зашифровки (более подробно см. основную статью). Шифр Плейфера использовался в тактических целях британскими вооружёнными силами во Второй Англо-Бурской войне и в Первой мировой войне, а также австралийцами и немцами во время Второй мировой войны. Причиной использования шифра Плейфера было то, что он достаточно быстр в применении и не требует никакого специального оборудования.
Шифр Хилла[править | править код]
Шифр Хилла, изобретённый в 1929 году Лестером С. Хиллом, является полиграммным шифром, который может использовать большие группы с помощью линейной алгебры. Каждой букве сперва сопоставляется число. Для латинского алфавита часто используется простейшая схема: A = 0, B =1, …, Z=25. Блок из n букв рассматривается как n-мерный вектор и умножается на n × n матрицу по модулю 26. Компоненты матрицы являются ключом, и должны быть случайными при условии, что матрица должна быть обратима в , чтобы была возможна операция расшифрования.[24] Шифр Хилла уязвим для атак на основе открытых текстов, потому что в нём используются линейные операции. Поэтому, для увеличения криптостойкости, в него должны быть добавлены какие-либо нелинейные операции. Комбинирование линейных операций, как в шифре Хилла, и нелинейных шагов привело к созданию подстановочно-перестановочной сети (например, сеть Фейстеля). Поэтому с определённой точки зрения можно считать современные блочные шифры, как вид полиграммных шифров.[25]
Криптоанализ[править | править код]
Известный американский криптограф Брюс Шнайер выделяет четыре 4 основных метода криптоанализа:[26]
- Атака на основе шифротекста
- Атака на основе открытых текстов
- Атака на основе подобранного открытого текста
- Атака на основе адаптивно подобранного открытого текста
Опишем криптостойкость шифров подстановки относительно данных методов.
Атаки на основе шифротекста[править | править код]
Моноалфавитные шифры легко вскрываются с использованием методов частотного анализа[6].
Криптоанализ однозвучных шифров подстановки осуществляется подсчетом частотностей появления пар и троек символов[27].
Для дешифровки полиалфавитных шифров применяется метод Касиски[28].
Полиграммный шифр Хилла может быть взломан при вычислении частотностей последовательностей символов[29].
Атаки на основе открытых текстов[править | править код]
При наличии открытого текста достаточной длины взлом моноалфавитных и однозвучных шифров является тривиальным[30].
Для быстрого взлома полиалфавитных шифров длина открытого текста должна превышать длину ключа[31].
Атаки на основе подобранного открытого текста[править | править код]
Для атак на основе выбранного открытого текста уязвимы все шифры подстановки за исключением одноразового блокнота[32].
Стандартный шифр Хилла, составленный из n линейных уравнений, может быть взломан по выбранному открытому тексту при перехвате криптоаналитиком n² пар символов сообщения и шифротекста.[25]
В шифровальных машинах[править | править код]


Одно из первых шифровальных устройств было придумано в XV веке и осуществляло замену шифром Цезаря. Его автором являлся итальянский архитектор Леоном Баттиста Альберти, который внес ощутимый вклад в развитие шифров подстановки. Данное устройство состояло из двух медных дисков разного размера, скрепленных иглой. По краям каждого диска наносился алфавит. Оба диска могли вращаться независимо друг от друга, тем самым сопоставляя буквы открытого и шифрованного текста. Диск Альберти широко использовался пять столетий, в том числе во время Гражданской войны в США[33].
В начале XX века после изобретения радио появилась необходимость разработки шифровальных машин для использования в военных и коммерческих целях. В качестве основы данных устройств использовались полиалфавитные шифры подстановки, а также принцип работы шифровального диска[34].
Для получения зашифрованного сигнала применялся полый диск с нанесенными с двух сторон контактами. Получаемый в результате шифрования текст зависел от коммутации диска и его углового положения. Данный вид шифровальных устройств впоследствии назвали роторными машинами[34][35].
Роторные машины применялись различными странами в ходе Второй мировой войны. Наиболее известными из них были: американская машина SIGABA, немецкая ENIGMA, английская TYPEX и японская PURPLE.[36]
Роторные шифровальные системы имели два вида ключей. Перепайки между контактами ротора задавали постоянный ключ. Для замены постоянных ключей необходимо было модернизировать все выпущенные шифровальные машины данной модели, что на практике тяжело реализуемо. Переменные ключи зачастую менялись каждый день и определялись набором роторов и их начальным положением.[37]
Применение в наше время[править | править код]
Несмотря на вытеснение шифров подстановки блочными шифрами, одноразовые блокноты по-прежнему применяются на государственном уровне в наше время. Они используются для обеспечения сверхсекретных каналов связи. По слухам, телефонная линия между главами СССР и США шифровалась с помощью одноразового блокнота и вполне возможно существует до сих пор. Одноразовые блокноты применяются шпионами различных государств для сокрытия особо важной информации. Такие сообщения невозможно расшифровать при отсутствии записанного в блокноте ключа независимо от вычислительной мощности ЭВМ.[38][12]
В литературе[править | править код]

- Шифром подстановки является известный шифр «Пляшущие человечки» из произведения Артура Конан Дойля. В нём символические фигурки людей заменяли буквы текста в посланиях.
- В рассказе Эдгара По «Золотой жук» главный герой Роберт Моррис пытается прочитать записку о кладе зашифрованную шифром подстановки.
- Один из героев повести О. Генри «Короли и капуста» отправляет сообщение «Президент Ангурии бежал с любовницей к океану», используя шифр подстановки.
- Шифр замены фигурирует в романе Жюль Верна «Путешествие к центру Земли».
- Шифр Атбаш встречается в романе Дэна Брауна «Код да Винчи».
- В романе «Криптономикон», написанном Нилом Стивенсоном, подробно описываются шифры времен Второй мировой войны.
В кинематографе[править | править код]
- Практическое использование шифров подстановки стратегической авиацией США демонстрируется в кинофильме «Доктор Стренджлав» режиссёра Стенли Кубрика. Пилот бомбардировщика, получив шифровку по радиосвязи, достает секретную кодовую таблицу и узнает с помощью неё содержание приказа.
- В художественном фильме «Шпион, выдавший ключ», офицер ВМФ США, передает секретные криптографические ключи агенту КГБ.
- В криминальном сериале Дэвида Саймона «Прослушка» злоумышленники используют оригинальный шифр подстановки, в котором цифры на телефонной клавиатуре заменяются на противоположные по расположению относительно клавиши «5».
- В мультсериале Gravity Falls активно используются шифр Атбаш, шифр Цезаря (ROT 3), шифр A1Z26 (в русском варианте — А1Я33) и шифр Виженера. Также там встречаются шифры символьной подстановки и комбинация шифров.
Примечания[править | править код]
- ↑ Алферов, 2002, с. 93.
- ↑ Бабаш, Шанкин, 2007, с. 12,47-48.
- ↑ Соболева, 2002, с. 7.
- ↑ Бабаш, Шанкин, 2007, с. 17.
- ↑ Долгов, Анисимов, 2008, с. 6—7.
- ↑ 1 2 Габидулин, 2011, с. 10—11.
- ↑ Бабаш, Шанкин, 2007, с. 24—26.
- ↑ Кан, 2000, с. 24,39.
- ↑ Сингх, 2007, с. 71—72.
- ↑ Бабаш, Шанкин, 2007, с. 26—29, 43-44.
- ↑ Сингх, 2007, с. 414—415.
- ↑ 1 2 Долгов, Анисимов, 2008, с. 9—10.
- ↑ Hoskisson.
- ↑ Wobst, 2001, p. 20.
- ↑ Ященко, 2012, с. 172.
- ↑ Шнайер, 2003, с. 57.
- ↑ Сингх, 2007, с. 70.
- ↑ Бабаш, 2002.
- ↑ Бабаш, Шанкин, 2007, с. 29.
- ↑ Бабаш, Шанкин, 2007, с. 43—44.
- ↑ Брюс_Шнайер, 2003, с. 26—28.
- ↑ Бабаш, Гольев.
- ↑ Алферов, 2002, с. 115.
- ↑ Hill, 1929, pp. 306—312.
- ↑ 1 2 Алферов, 2002, с. 116—119.
- ↑ Шнайер, 2002, с. 20.
- ↑ Долгов, Анисимов, 2008, с. 33.
- ↑ Габидулин, 2011, с. 33—34.
- ↑ Габидулин, 2011, с. 30.
- ↑ Смарт, 2005, с. 95.
- ↑ Габидулин, 2011, с. 45.
- ↑ Смарт, 2005, с. 105—106.
- ↑ Сингх, 2007, с. 146.
- ↑ 1 2 Сингх, 2007, с. 149.
- ↑ Бабаш, Шанкин, 2007, с. 105—109.
- ↑ Долгов, Анисимов, 2008, с. 34.
- ↑ Долгов, Анисимов, 2008, с. 35.
- ↑ Брюс_Шнайер, 2003, с. 27—28.
Литература[править | править код]
- Книги и монографии
- Саймон Сингх. Книга шифров. Тайная история шифров и их расшифровки. — АСТ, 2007. — ISBN 978-5-17-038477-8.
- Брюс Шнайер. Секреты и ложь. Безопасность данных в цифровом мире. — Издательский дом «Питер», 2003. — 368 с. — ISBN 5-318-00193-9.
- В. В. Ященко. Введение в криптографию. — МЦНМО, 2012. — 348 с. — ISBN 978-5-4439-0026-1.
- А. П. Алферов, А. Ю. Зубов, А. С. Кузьмин, А. В. Черемушкин. Основы криптографии: Учебное пособие. — Гелиос АРВ, 2002. — 480 с. — ISBN 5-85438-025-0.
- А.В. Бабаш, Г.П. Шанкин. Криптография. — Солон-пресс, 2007. — 512 с. — ISBN 5-93455-135-3.
- Брюс Шнайер. Прикладная криптография = Applied Cryptography / Перевод с английского Дубнова Н.. — 2-ое. — Диалектика, 2003. — 610 с. — ISBN 5-89392-055-4.
- Reinhard Wobst. Cryptology Unlocked. — Wiley, 2001. — ISBN 978-0470060643.
- А.В. Бабаш, Г.П. Шанкин. История криптографии. Часть I. — Гелиос АРВ, 2002. — 240 с. — ISBN 5-85438-043-9..
- Дэвид Кан. Взломщики кодов = The Codebreakers – The Story of Secret Writing / Перевод с английского А. Ключевский. — 2-ое. — М.: Центрполиграф, 2000. — 473 с. — ISBN 5-227-00678-4.
- В.А. Долгов, В.В. Анисимов. Криптографические методы защиты информации. — ДВГУПС, 2008. — 155 с.
- Т.А. Соболева. История шифровального дела в России.. — ОЛМА-ПРЕСС Образование, 2002. — 511 с. — ISBN 5-224-03634-8.
- Н. Смарт. Криптография = Cryptography / Перевод с английского С.А. Кулешова. — Техносфера, 2005. — 528 с. — ISBN 5-94836-043-1.
- Э.М. Габидулин, А.С. Кшевецкий, А.И. Колыбельников. Защита информации: учебное пособие. — МФТИ, 2011. — 255 с. — ISBN 5-7417-0377-9.
- Отдельные статьи и главы
- Lester S. Hill. Cryptography in an Algebraic Alphabet // The American Mathematical Monthly. — 1929. — Vol. 36, № 6.
- Шнайер Б. Криптоанализ // Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си = Applied Cryptography. Protocols, Algorithms and Source Code in C. — М.: Триумф, 2002. — С. 19—22. — 816 с. — 3000 экз. — ISBN 5-89392-055-4.
Ссылки[править | править код]
- Русскоязычные статьи в Internet
- А. В. Бабаш, Г. П. Шанкин. Средневековая криптография (2013). Дата обращения: 13 апреля 2013. Архивировано из оригинала 21 мая 2013 года.
- А. В. Бабаш, Ю. И. Гольев, Д. А. Ларин, Г. П. Шанкин. Криптографические идеи XIX века (2013). Дата обращения: 13 апреля 2013. Архивировано из оригинала 17 мая 2009 года.
- Англоязычные статьи и ресурсы в Internet
- Paul Y. Hoskisson. Jeremiah's Game (2013). Дата обращения: 13 апреля 2013. Архивировано из оригинала 1 июля 2013 года.

