0,(9)

0,(9) или 0,999… (, ) («ноль и девять в периоде») — периодическая десятичная дробь, представляющая число 1. Другими словами,
Существует много доказательств этого равенства.
Несмотря на то, что правильность этого равенства является доказанным фактом и не вызывает сомнений в научном сообществе, многие люди пытаются доказать обратное. В таких доказательствах обычно допускаются арифметические и логические ошибки. Такое ярое несогласие вызвано тем, что данное равенство противоречит интуиции. Из-за этого оно приобрело большую популярность.
Пояснение[править | править код]
При использовании математических обозначений стоит понимать, что обозначения — это не есть сам предмет обсуждения, а всего лишь его обозначение. Два обозначения вполне могут обозначать один и тот же предмет. К примеру, запись и обозначают одно и то же число. Хоть это и разные записи, задают они один и тот же объект. Другой пример — и . На этом примере видно, что разные обыкновенные дроби вполне могут задавать одно и то же число, и, таким образом, запись в виде обыкновенной дроби неоднозначна.
Тот факт, что запись в виде конечной десятичной дроби однозначна, является особенностью именно конечных дробей. Разные конечные дроби обозначают разные числа. Но работает это свойство только для конечного случая. В общем случае (где допускаются и конечные, и бесконечные десятичные дроби) две различные десятичные дроби могут представлять одно и то же число. Это связано с тем, что бесконечные дроби являются весьма непростым объектом, и многие свойства конечных на них не работают или работают не так. Примером такого неоднозначного представления являются и . Несмотря на то, что запись у них разная, они представляют собой одно и то же число, аналогично тому, как и представляют одно число.
Элементарные доказательства[править | править код]
Деление столбиком[править | править код]
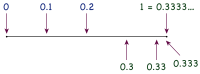
Обыкновенная дробь (например, ) может быть представлена в десятичном виде как конечная либо периодическая десятичная дробь. Перевод из обыкновенной дроби в десятичную может быть выполнен при помощи деления в столбик. Выполнив деление столбиком целого числа 1 на целое число 3, получим число 0,333… (в десятичной записи), в котором цифры 3 повторяются бесконечно:
Умножим левую часть на 3.
Умножим правую часть на 3. Заметим, что умножение каждой тройки на 3 даёт девятку:
Таким образом,
- [1].
Аналогично можно доказать это равенство раскладывая в десятичную дробь не , а, например, :
Манипуляции с цифрами[править | править код]
Предыдущее доказательство было получено при помощи деления в столбик, что является алгоритмом перевода обыкновенной дроби в десятичную. Можно пойти в обратную сторону и воспользоваться алгоритмом перевода периодической десятичной дроби в обыкновенную.
Обозначим число за . При умножении десятичного числа на число цифры не меняются, запятая передвигается на одну цифру вправо:
То есть,
Если отнять из число , то все девятки после запятой вычтутся и останутся нули:
Вспомним про введённые обозначения через и заменим на них левую часть равенства:
Тогда,
и
- .
А так как за мы обозначали , то
- .
Строгое обоснование[править | править код]
Несмотря на простоту и понятность вышеприведённых доказательств, они не обладают достаточной математической строгостью и формальностью. Первое доказательство основано на том факте, что
- ,
второе на
- .
Эти выражения выглядят очевидными, однако очевидность обманчива, что можно видеть на примере самого равенства . При строгом изложении данные факты также требуют доказательства. Действительно, если для бесконечных десятичных дробей могут выполняться такие странные равенства, с чего нам вообще быть уверенными, что правила умножения для них работают так же, как и для конечных? Простота и очевидность доказательств выше достигается за счёт нестрогости рассуждений, что для контринтуитивных утверждений является существенным.
Для того, чтобы внести строгость в рассуждение, необходимо сначала разобраться что вообще означает запись . Рассмотрим какую-нибудь конечную десятичную дробь, например . Что означает эта запись? Данная запись есть сокращение для следующего выражения:
Число, которое обозначает эта запись, есть результат этого выражения. Так в математике определяется само понятие десятичная дробь. Согласно данному определению бесконечная десятичная дробь — точно такое же сокращение для такой суммы, отличающееся от конечного случая лишь тем, что количество слагаемых в ней бесконечно. То есть, например, дробь есть краткая запись для
- .
Рассматриваемая же в этой статье дробь есть краткая запись для суммы
- .
Число, которое обозначается записью , есть по определению сумма бесконечного числа слагаемых, представленных выше. Стоит понимать, что есть всего лишь формальная запись для результата вышеприведённой суммы, не обязанная удовлетворять каким-то свойствам, кроме равенства той сумме. Чему эта сумма окажется равна, тому и будет равно это число, вне зависимости от интуитивности этого или соответствия нашим ожиданиям.
Результат суммирования бесконечного числа слагаемых в математическом анализе определяется при помощи понятия предела. Свойства бесконечных сумм во многом отличаются от свойств конечных и требуют особой осторожности при их применении.
Последовательность представляет собой геометрическую прогрессию, знаменатель которой равен , а первый член — . По известной в математическом анализе формуле сумма геометрической прогрессии есть , где — первый член, а — знаменатель. Тогда
Данное доказательство основано лишь на формальном определении десятичной дроби и не содержит в себе использования каких-либо недоказанных свойств бесконечных десятичных дробей.
Такое доказательство (об эквивалентности чисел 10 и 9,999…) было опубликовано в 1770 году Леонардом Эйлером в издании «Элементы алгебры»[2].
Формула суммы сходящейся геометрической прогрессии была известна до Эйлера. В выпущенном в 1811 году учебнике «An Introduction to Algebra» также используется геометрическая прогрессия для числа 0,(9)[3]. В XIX веке реакция на такое правило суммирования вылилась в утверждение о том, что сумма ряда должна быть пределом последовательности частичных сумм[4].
Строгость элементарных доказательств[править | править код]
Используя формальное определение десятичной дроби, можно попытаться достигнуть достаточной строгости для первых двух доказательств.
Доказательство через деление в столбик использует нетривиальный факт, что деление в столбик даёт правильное представление в виде периодической дроби, что в свою очередь требует доказательства. Свойство же доказывается весьма просто с использованием операции умножения числовых рядов на число:
- .
Доказательство через манипуляции с цифрами использует два несложных свойства. Первое:
Второе: .
В любом случае, погоня за строгостью приведёт либо к необходимости манипуляций с числовыми рядами, либо к другому более искусственному определению периодических дробей. Реализацией второго подхода может стать, например, определение значения периодических дробей с помощью алгоритма перевода их в обыкновенные. Все свойства по-прежнему будут требовать доказательства, однако уже без необходимости прибегать к теории числовых рядов. Попытка реализации второго подхода определением периодических дробей через деление в столбик к нужному результату не приведёт, так как делением в столбик нельзя получить дробь с периодом .
Другие конечные десятичные дроби[править | править код]
Аналогичное равенство можно получить для любой конечной десятичной дроби. Пусть — некоторая конечная десятичная дробь, . Тогда:
Квадратные скобки здесь означают, что мы записываем вместо них цифру, равную . К примеру, , , , . Таким образом, для любой конечной десятичной дроби можно получить вторую десятичную запись с девятью в периоде. Это работает и наоборот: для каждой дроби с девятью в периоде можно получить конечную запись.
Интересным является тот факт, что все неоднозначности десятичной записи исчерпываются этим случаем. Дадим строгую формулировку этого факта. Прежде всего нужно строго определить какие записи мы считаем одинаковыми, а какие разными (чтобы не посчитать разными например записи и , или и ). Две десятичных записи будем считать одинаковыми, если у них совпадают цифры во всех разрядах (если какого-то разряда в записи нет, то будем считать его значение нулём). Тогда:
- если число ненулевое и допускает представление в виде конечной десятичной дроби, то оно допускает представление и с 9 в периоде;
- если число ненулевое и допускает представление с 9 в периоде, то оно допускает представление и в виде конечной десятичной дроби
- причём эти представления связаны соотношением
- ,
- других десятичных представлений у таких чисел нет;
- все остальные вещественные числа допускают только одно представление в виде десятичной дроби.
Сравнение десятичных дробей[править | править код]
Для конечных десятичных дробей существует простой алгоритм их сравнения. Идём слева направо до первого несовпадающего разряда. То число, у которого этот разряд больше, и оказывается большим. Если же все разряды равны, то и числа равны.
С бесконечными дробями этот алгоритм уже не работает. По этому алгоритму число должно было бы быть больше, чем , но эти числа равны. Однако алгоритм всё ещё работает для нестрогого сравнения: если в нём заменить все строгие неравенства на нестрогие, он будет работать и для бесконечных дробей. Таким образом, для и он выдаст , что верно.
При необходимости сравнить бесконечные десятичные дроби нужно учесть, что случаем девяти в периоде исчерпываются все неоднозначные представления чисел. Таким образом, можно просто заранее привести все числа с девяткой в периоде к конечной записи и применить обычный алгоритм сравнения.
Другие системы счисления[править | править код]
Аналогичное равенство можно получить для любой позиционной системы счисления. Для системы счисления с основанием и старшей цифрой конечная дробь , может быть представлена как
- .
К примеру: , , , .
Все свойства сохраняются и для других систем счисления. Точно так же каждая конечная дробь допускает представление в виде дроби с периодом и наоборот, причём двумя этими представлениями исчерпываются все представления числа. Остальные дроби имеют только одно представление. Те же самые замечания верны для поразрядного сравнения дробей.
Особенность других систем счисления заключается в том, что дроби, представимые в десятичной системе счисления конечной дробью, могут представляться периодической в другой системе счисления, и наоборот. Так, дробь , непредставимая в десятичной системе счисления как конечная дробь, в троичной представляется как . Дробь в троичной системе представляется как . Таким образом, количество представлений определённого числа в виде n-ричной дроби, зависит от системы счисления. Число в виде десятичной дроби имеет два представления: и , а в виде троичной только одно: . Число в виде десятичной дроби имеет одно представление: , а в виде троичной два: и .
Зависимость количеств n-ричных представлений от системы счисления проявляется только для нецелых рациональных чисел. Все целые числа кроме нуля имеют в любой системе счисления по два представления, все иррациональные и — одно.
Применение[править | править код]
Равенство находит применение, например, в элементарной теории чисел. В 1802 году H. Goodwin опубликовал наблюдение, обнаруженное им при делении чисел на простые числа. Например:
- = 0,142857142857… и
- 142 + 857 = 999;
- = 0,0136986301369863… и
- 0136 + 9863 = 9999.
Миди (M. E. Midy) в 1836 году обобщил данные наблюдения до теоремы Миди.
В популярной культуре[править | править код]
Автор новостной колонки «The Straight Dope» доказывает равенство 1 = 0,999… с помощью дроби 1⁄3 и пределов, говоря о непонимании:
Низший примат в нас упирается, говоря: ,999~ на самом деле представляет не число, а процесс. Чтобы найти число мы должны остановить этот процесс. И в этот момент равенство ,999~ = 1 просто разваливается. Чушь.
Оригинальный текст (англ.)The lower primate in us still resists, saying: .999~ doesn't really represent a number, then, but a process. To find a number we have to halt the process, at which point the .999~ = 1 thing falls apart. Nonsense.— [5].
Вопрос о равенстве 1 = 0,999… стал такой популярной темой в первые семь лет форумов «Battle.net», что компания «Blizzard Entertainment» выпустила «пресс-релиз» на День дураков 2004 года:
Мы очень рады закрыть книгу на этой теме раз и навсегда. Мы были свидетелями страдания и беспокойства насчёт того, ,999~ равняется 1 или же нет, и мы с гордостью представляем следующее доказательство, решающее эту проблему для наших покупателей[6].
Далее следуют доказательства, основанные на пределах и умножении на число 10.
См. также[править | править код]
- Ахиллес и черепаха
- Бесконечно малая и бесконечно большая
- Неоднозначность представления чисел в виде десятичных дробей
- -0 и +0
- 0.(9) = 9/10¹ + 9/10² … + 9/10^n - это сходящийся ряд (математика).
Примечания[править | править код]
- ↑ Сравните с версией этого же аргумента в двоичной системе счисления из книги Silvanus P. Thompson «Calculus made easy» (St. Martin’s Press, New York, 1998, ISBN 0-312-18548-0).
- ↑ Страница 179 книги Эйлера.
- ↑ Страница 69 книги Grattan-Guinness; страница 177 книги Bonnycastle.
- ↑ См., например, страницу 706 книги J. Stewart, страницу 61 книги Rudin, страницу 213 книги Protter и Morrey, страницу 180 книги Pugh, страницу 31 книги J. B. Conway.
- ↑ Cecil Adams. An infinite question: Why doesn't .999~ = 1? (англ.). The Straight Dope. Chicago Reader (11 июля 2003). Дата обращения: 6 сентября 2006. Архивировано из оригинала 18 февраля 2012 года.
- ↑ Blizzard Entertainment:Press Releases (англ.). Дата обращения: 17 июня 2015. Архивировано 17 июня 2015 года.
В другом языковом разделе есть более полная статья 0.999... (англ.). |


















































}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7871d6d39d624fa4e8be4f212d08a6df8e270302)












}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d44d42871ce7a622c0a59b5e284332d5d81ac874)












