Квадруполь
В теории поля представление системы зарядов в виде некоторых квадрупо́лей, аналогично представлению её в виде системы диполей, используется для приближённого расчёта создаваемого ей поля и излучения. Более общим представлением является разложение системы на мультиполи, соответствующее разложению потенциалов в ряд Тейлора по некоторым переменным. Квадруполь — частный случай мультиполя. Квадрупольное рассмотрение системы оказывается особенно важным в том случае, когда её дипольный момент и заряд равны 0.
Электрический квадруполь[править | править код]

Электрический квадруполь (от лат. quadrum — четырёхугольник, квадрат и др.-греч. πόλος — полюс), система заряженных частиц, полный электрический заряд и электрический дипольный момент которой равны нулю. Квадруполь можно рассматривать как совокупность двух одинаковых диполей с равными по величине и противоположными по направлению дипольными моментами, расположенных на некотором расстоянии друг от друга (см. рис.). На больших расстояниях от квадруполя напряженность его электрического поля убывает обратно пропорционально четвёртой степени , а зависимость от зарядов и их расположения описывается в общем случае набором из пяти независимых величин, которые, вместе составляют квадрупольный момент системы. Квадрупольный момент определяет также энергию квадруполя во внешнем электрическом поле. Квадруполь является мультиполем 2-го порядка.
Квадрупольный момент (произвольной) системы зарядов является тензором 2-го ранга в . Он представляется интегралом по пространству
- ,
где — плотность зарядов в данной точке, — модуль радиус-вектора, , — индексы, нумерующие координаты.
Тензор квадрупольного момента симметричен:
Его след равен нулю:
Здесь и далее используется соглашение Эйнштейна о суммировании.
Если полный заряд системы и её дипольный момент равны 0, то квадрупольный момент не зависит от выбора начала координат. В противном случае необходимо также указывать центр квадруполя — начало координат при его вычислении.
Поле квадруполя[править | править код]
На больших расстояниях поле любой в целом нейтральной системы зарядов, дипольный момент которой равен нулю, выглядит как поле некоторого (возможно, изменяющегося со временем) квадруполя или более высокого мультиполя (октуполя и т.д.). Рассмотрение системы как некоторого квадруполя может иметь смысл и тогда, когда дипольный момент и/или заряд системы не равны нулю, если раскладывать создаваемый потенциал в ряд по мультиполям. Квадрупольное излучение системы на больших расстояниях равно (в СГС)
Здесь — скорость света, — полная мощность излучения. Во многих случаях достаточно считать, что излучение системы складывается из дипольного, квадрупольного и магнитодипольного.
Квадрупольный потенциал имеет вид (при определении квадрупольного момента так, как описано выше):
Здесь — радиус-вектор точки, в которой берётся потенциал, относительно центра квадруполя. является вторым членом разложения потенциала в ряд по расстоянию до начала координат.
Поле электрического квадруполя имеет ярко выраженный нецентральный характер, и его удобно представлять, используя тензорную форму записи[1]:
Магнитный квадруполь[править | править код]

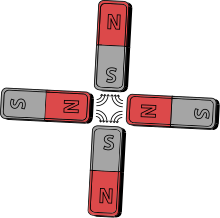
Все известные магнитные источники дают поля диполя. Однако, возможно создать магнитный квадруполь путём помещения четырёх идентичных стержневых магнитов перпендикулярно друг другу таким образом, что северный полюс одного магнита находится рядом с южным полюсом другого. Такая конфигурация убирает дипольный момент и даёт квадрупольный момент, а поля системы убывают на больших расстояниях быстрее, чем поля диполя.
Пример магнитного квадруполя, содержащего постоянные магниты, представлен на картинке справа. Электромагниты подобного концептуального дизайна (квадрупольные линзы) обычно используются для фокусировки пучков заряженных частиц в ускорителях заряженных частиц. Метод известен под названием сильная фокусировка.
Изменяющийся магнитный квадрупольный момент вызывает электромагнитное излучение.
Гравитационный квадруполь[править | править код]
См. также[править | править код]
- Букингем (единица измерения)
- Диполь (электродинамика)
- Мультиполь
- высокочастотный квадруполь, см. Квадрупольный масс-анализатор#Принцип действия
Примечания[править | править код]
- ↑ В.И. Денисов, Лекции по электродинамике §11 (2007)
Литература[править | править код]
- Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7. — § 41.
















