Можно ли услышать форму барабана?

Первый пример двух неконгруэнтных барабанов, звучащих одинаково. Обратите внимание, что фигуры имеют равные площади и периметры

«Можно ли услышать форму барабана?» — вопрос Липмана Берса, восходящий к Герману Вейлю.

Частоты, на которых барабанная мембрана может вибрировать, однозначно зависят от его формы. Спрашивается: однозначно ли можно восстановить форму барабана, если все его частоты известны?

Формулировка «Можно ли услышать форму барабана?» появляется в статье Марка Каца, опубликованной в 1966 году. Эта статья популяризовала вопрос и таким образом сыграла заметную роль в развитии математики на несколько десятилетий. За неё Кац был удостоен премии Форда в 1967 году и премии Шовенэ в 1968 году.

Формулировка

Барабан мыслится как плоская область $D$, граница которой фиксирована. Обозначим через $\lambda _{n}$ её n-ое собственное значение для лапласиана с условием Дирихле на границе. То есть нас интересуют значения $\lambda$, для которых существует функция $u\colon D\to \mathbb {R}$ такая, что

${\begin{cases}\Delta u+\lambda u=0,\\u|_{\partial D}=0.\end{cases}}$

Две области называются изоспектральными, если они имеют одинаковые собственные значения, учитывая кратность.

Поэтому вопрос можно переформулировать так:

• Существуют ли две изоспектральные и неконгруэнтные области?

Вариации

Аналогичные вопросы можно задать про уравнения Лапласа на областях в старших размерностях, также на римановых многообразиях и для других эллиптических дифференциальных операторов, таких как оператор Коши — Римана или оператор Дирака. Можно накладывать другие граничные условия, в частности условие Неймана.

Ответы

Плоские торы

Почти сразу Джон Милнор построил пару изоспектральных неизометричных 16-мерных торов. Позже подобные примеры были построены во всех размерностях начиная с четырёх. При этом в размерностях 2 и 3 таких примеров не существует. Трёхмерный случай потребовал серьёзных компьютерных вычислений.

Таким образом, «форму плоского тора нельзя услышать полностью в размерностях 4 и выше».

Области на плоскости

Однопараметрическое семейство пар изоспектральных барабанов. Каждый из двух барабанов составлен из 7 равных треугольников

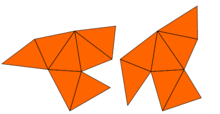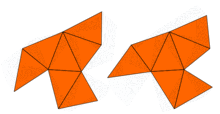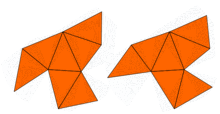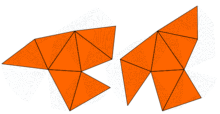
В 1992 году Гордон, Уэбб и Уолперт построили пару неконгруэнтных изоспектральных невыпуклых многоугольников (см. рисунок).

Доказательство того, что оба многоугольника имеют одинаковые собственные значения, использует симметрии и вполне элементарно. Короткое доказательство более общего утверждения приведено в книге Конвея.

Таким образом, «форму барабана нельзя услышать полностью».

Частные случаи

Вместе с тем, многие характеристики этой формы восстановимы.

• Согласно формуле Вейля, площадь может быть однозначно восстановлена по спектру.
  • По теореме Иврия тоже верно и для периметров областей с гладкой границей.
• Если область выпукла, а её граница аналитическая, то спектр позволяет однозначно установить её форму.
  • Вопрос остаётся открытым для невыпуклых областей с аналитической границей.
• Известно, что множество изоспектральных областей компактно в $C^{\infty }$-топологии.
• По теореме сравнения Чжэна сфера является спектрально-жёсткой; то есть, многообразие с тем же спектром, что и у сферы, должно быть ей изометрично.

Литература

• Конвей Дж. Квадратичные формы, данные нам в ощущениях. — М.: МЦНМО, 2008. — 144 с. — 1000 экз. — ISBN 978-5-94057-268-8.

Ссылки

• Титаренко С. А. Клеточность как необходимое условие спектральной задачи для лапласиана «‎услышать форму барабана». — Дифференциальные уравнения и математическое моделирование, 2022. — 103-107 с.
• Титаренко С. А. Можно услышать форму почти любого барабана! — Preprints of the St. Petersburg Mathematical Society, 2020. — 11 с.
• Some planar isospectral domains by Peter Buser, John Horton Conway, Peter Doyle, and Klaus-Dieter Semmler
• Weisstein, Eric W. Isospectral Manifolds (англ.) на сайте Wolfram MathWorld.
• Benguria, Rafael D. (2001), "Dirichlet eigenvalue", in Hazewinkel, Michiel (ed.), Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4