Обратный маятник

Перевёрнутый маятник — устройство, представляющее собой маятник, который имеет центр масс выше своей точки опоры, закреплённый на конце жёсткого стержня. Часто точка опоры закрепляется на тележке, которая может перемещаться по горизонтали. В то время как нормальный маятник устойчиво висит вниз, обратный маятник по своей природе неустойчивый и должен постоянно балансироваться чтобы оставаться в вертикальном положении, с помощью применения крутящего момента к опорной точке или при перемещении точки опоры по горизонтали, как части обратной связи системы. Простейшим демонстрационным примером может являться балансировка карандаша на конце пальца.
Обзор[править | править код]
Перевёрнутый маятник является классической проблемой динамики и теории управления и широко используется в качестве эталона для тестирования алгоритмов управления (ПИД-регуляторов, нейронных сетей, нечёткого управления и т. д.).
Проблема обратного маятника связана с наведением ракет, так как двигатель ракеты расположен ниже центра тяжести, вызывая нестабильность.[1] Эта же проблема решена, например, в сегвее, самобалансирующемся транспортном устройстве.
Другим способом стабилизации обратного маятника является быстрое колебание основания в вертикальной плоскости. В этом случае можно обойтись без обратной связи. Если колебания достаточно сильные (в смысле величины ускорения и амплитуды), то обратный маятник может стабилизироваться. Если движущаяся точка колеблется в соответствии с простыми гармоническими колебаниями, то движение маятника описывается функцией Матьё.
Уравнения движения[править | править код]
С неподвижной точкой опоры[править | править код]
Уравнение движения аналогично прямому маятнику за исключением того, что знак углового положения измеряется от вертикальной позиции неустойчивого равновесия:
При переносе он будет иметь тот же знак углового ускорения:
Таким образом, обратный маятник будет ускоряться от вертикального неустойчивого равновесия в противоположную сторону, а ускорение будет обратно пропорционально длине. Высокий маятник падает медленнее, чем короткий.
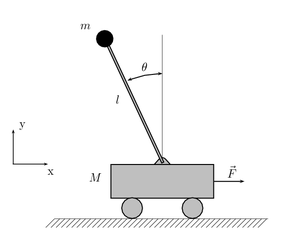
Маятник на тележке[править | править код]
Уравнения движения могут быть получены с использованием уравнений Лагранжа. Речь идёт об приведённом выше рисунке, где угол маятника длиной по отношению к вертикали и действующей силе гравитации и внешних сил в направлении . Определим положение тележки. Лагранжиан системы:
где является скоростью тележки, а - скорость материальной точки . и может быть выражена через и путём записи скорости как первой производной положения.
Упрощение выражения приводит к:
Лагранжиан теперь определяется по формуле:
и уравнения движения:
Подстановка в эти выражения с последующим упрощением приводит к уравнениям, описывающим движение обратного маятника:
Эти уравнения являются нелинейными, но, поскольку цель системы управления - удерживать маятник вертикально, то уравнения можно линеаризовать, приняв .
Маятник с колеблющимся основанием[править | править код]
Уравнение движения для такого маятника связано с безмассовой осциллирующей базой и получено так же, как для маятника на тележке. Положение материальной точки определяется по формуле:
и скорость найдена через первую производную позиции:
Лагранжиан для этой системы можно записать в виде:
уравнения движения следуют из:
в результате:
Если y колеблется в соответствии с простыми гармоническими колебаниями, , то получаем дифференциальное уравнение:
Это уравнение не имеет элементарного решения в замкнутом виде, но может быть изучено во множестве направлений. Оно близкого к уравнению Матье, например, когда амплитуда колебаний мала. Анализ показывает, что маятник остается в вертикальном положении при быстрых колебаниях. Первый график показывает, что при медленно колеблющимся , маятник быстро падает, после выхода из устойчивого вертикального положения.
Если быстро колеблется, то маятник может быть стабилен около вертикальной позиции. Второй график показывает, что, после выхода из устойчивого вертикального положения, маятник теперь начинается колебаться вокруг вертикальной позиции ().Отклонение от вертикального положения остается мало, и маятник не падает.
Применение[править | править код]
Примером является балансировка людей и предметов, например в акробатике или катание на одноколесном велосипеде. А также сегве́й — электрический самобалансирующийся самокат с двумя колёсами.

Перевернутый маятник был центральным компонентом в разработке нескольких ранних сейсмографов[2].
См. также[править | править код]
Ссылки[править | править код]
- ↑ Rocket Stability. Дата обращения: 23 апреля 2012. Архивировано из оригинала 7 июня 2013 года.
- ↑ The Early History of Seismometry (to 1900). Дата обращения: 30 сентября 2017. Архивировано из оригинала 27 августа 2016 года.
- D. Liberzon Switching in Systems and Control (2003 Springer) pp. 89ff
Дальнейшее чтение[править | править код]
- Franklin; et al. (2005). Feedback control of dynamic systems, 5, Prentice Hall. ISBN 0-13-149930-0































