Гармонические колебания

Гармони́ческие колеба́ния — колебания, при которых физическая величина изменяется с течением времени по гармоническому (синусоидальному, косинусоидальному) закону.
Математическое описание[править | править код]
Уравнение гармонического колебания имеет вид
или
- ,
где
- — отклонение колеблющейся величины в текущий момент времени от среднего за период значения (например, в кинематике — смещение, отклонение колеблющейся точки от положения равновесия);
- — амплитуда колебания, то есть максимальное за период отклонение колеблющейся величины от среднего за период значения, размерность совпадает с размерностью ;
- (радиан/с, градус/с) — циклическая частота, показывающая, на сколько радиан (градусов) изменяется фаза колебания за 1 с;
- (радиан, градус) — полная фаза колебания (сокращённо — фаза, не путать с начальной фазой);
- (радиан, градус) — начальная фаза колебаний, которая определяет значение полной фазы колебания (и самой величины ) в момент времени .
Дифференциальное уравнение, описывающее гармонические колебания, имеет вид
Любое нетривиальное[1] решение этого дифференциального уравнения — гармоническое колебание с циклической частотой .
Примеры[править | править код]
При равномерном движении точки по окружности гармоническое колебание совершает проекция (ортогональная) этой точки на любую прямую, лежащую в той же плоскости[2]. Колебания, близкие к гармоническим, совершает под действием силы тяготения маленький грузик, подвешенный на тонкой длинной нити — математический маятник — при малых амплитудах[3]. Гармонические колебания под действием силы упругости совершает закреплённый между двумя пружинами на горизонтальной направляющей грузик[4]. Гармоническими являются крутильные колебания раскручивающегося под действием силы упругости подвешенного вертикально грузика, такие же колебания совершает балансир механических часов[5].
Вообще, материальная точка совершает гармонические колебания, если они происходят в результате воздействия на точку силы, пропорциональной смещению колеблющейся точки от положения равновесия и направленной противоположно этому смещению.
Примеры гармонических колебаний имеются не только в механике — так, в LC-контуре без диссипативных потерь изменения заряда на ёмкости, напряжения и тока в цепи со временем происходят по гармоническому закону.
Виды колебаний[править | править код]
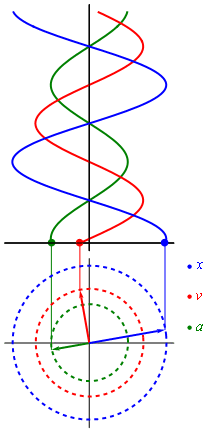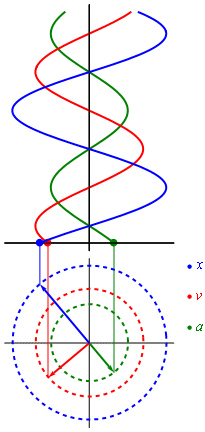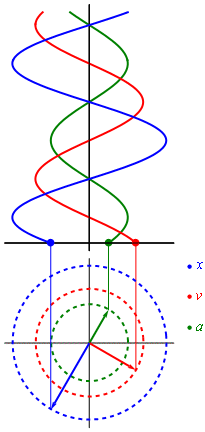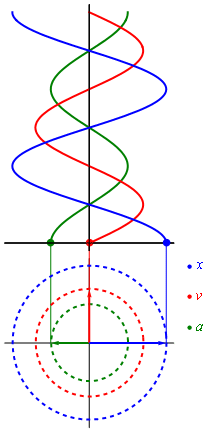
- Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Чтобы свободные колебания были гармоническими, необходимо, чтобы колебательная система была линейной (описывалась линейными уравнениями движения), и в ней отсутствовала диссипация энергии (при ненулевой диссипации, в системе после возбуждения происходят затухающие колебания).
- Вынужденные колебания совершаются под воздействием внешней периодической силы. Чтобы вынужденные колебания были гармоническими, достаточно, чтобы колебательная система была линейной (описывалась линейными уравнениями движения), а внешняя сила (воздействие) менялась со временем как гармоническое колебание (то есть, чтобы зависимость от времени этой силы тоже, в свою очередь, была синусоидальной).
Применение[править | править код]
Гармонические колебания выделяются из всех остальных видов колебаний по следующим причинам:
- Очень часто[6] малые колебания, как свободные, так и вынужденные, которые происходят в реальных системах, можно считать имеющими форму гармонических колебаний или очень близкую к ней.
- Как установил в 1822 году Фурье, широкий класс периодических функций может быть разложен на сумму тригонометрических компонентов — в ряд Фурье. Другими словами, любое периодическое колебание может быть представлено как сумма гармонических колебаний с соответствующими амплитудами, частотами и начальными фазами. Среди слагаемых этой суммы существует гармоническое колебание с наименьшей частотой, которая называется основной частотой, а само это колебание — первой гармоникой или основным тоном, частоты же всех остальных слагаемых, гармонических колебаний, кратны основной частоте, и эти колебания называются высшими гармониками или обертонами — первым, вторым и т.д.[7]
- Для широкого класса систем откликом на гармоническое воздействие является гармоническое колебание (свойство линейности), при этом связь воздействия и отклика является устойчивой характеристикой системы. С учётом предыдущего свойства это позволяет исследовать прохождение колебаний произвольной формы через системы.
См. также[править | править код]
- Гармонический осциллятор
- Математический маятник
- Физический маятник
- Псевдогармонические колебания
- Биения
Примечания[править | править код]
- ↑ То есть не равное тождественно нулю.
- ↑ Ландсберг, 2003, с. 17.
- ↑ Ландсберг, 2003, с. 2,25.
- ↑ Ландсберг, 2003, с. 27—29.
- ↑ Ландсберг, 2003, с. 29—30.
- ↑ Подразумеваемым условием здесь является то, что свойства системы должны быть постоянны во времени (что в реальности достаточно часто выполняется, по крайней мере, приближенно).
- ↑ Ландсберг, 2003, с. 43.
Литература[править | править код]
- Элементарный учебник физики / Под ред. Г.С. Ландсберга. — 13-е изд. — М.: ФИЗМАТЛИТ, 2003. — Т. 3. Колебания и волны. Оптика. Атомная и ядерная физика.
- Хайкин С. Э. Физические основы механики. — М., 1963.
- А. М. Афонин. Физические основы механики. — Изд. МГТУ им. Баумана, 2006.
- Горелик Г. С. Колебания и волны. Введение в акустику, радиофизику и оптику. — М.: Физматлит, 1959. — 572 с.









