Игра «Жизнь»

Игра «Жизнь» (англ. Game of Life) — клеточный автомат, придуманный английским математиком Джоном Конвеем в 1970 году.[1] Это игра без игроков[2][3], в которой человек создаёт начальное состояние, а потом лишь наблюдает за её развитием. В игре можно создать процессы с полнотой по Тьюрингу, что позволяет реализовать любую машину Тьюринга.
Правила[править | править код]

- Место действия игры — размеченная на клетки плоскость, которая может быть безграничной, ограниченной или замкнутой.
- Каждая клетка на этой поверхности имеет восемь соседей, окружающих её, и может находиться в двух состояниях: быть «живой» (заполненной) или «мёртвой» (пустой).
- Распределение живых клеток в начале игры называется первым поколением. Каждое следующее поколение рассчитывается на основе предыдущего по таким правилам:
- в пустой (мёртвой) клетке, с которой соседствуют три живые клетки, зарождается жизнь;
- если у живой клетки есть две или три живые соседки, то эта клетка продолжает жить; в противном случае (если живых соседей меньше двух или больше трёх) клетка умирает («от одиночества» или «от перенаселённости»).
- Игра прекращается, если
- на поле не останется ни одной «живой» клетки;
- конфигурация на очередном шаге в точности (без сдвигов и поворотов) повторит себя же на одном из более ранних шагов (складывается периодическая конфигурация)
- при очередном шаге ни одна из клеток не меняет своего состояния (частный случай предыдущего правила, складывается стабильная конфигурация)
Игрок не принимает активного участия в игре. Он лишь расставляет или генерирует начальную конфигурацию «живых» клеток, которые затем изменяются согласно правилам. Несмотря на простоту правил, в игре может возникать огромное разнообразие форм.
Появление идеи[править | править код]
Джон Конвей ещё в детстве заинтересовался проблемой, предложенной в 1940-х годах известным математиком Джоном фон Нейманом, который пытался создать гипотетическую машину, способную воспроизводить себя. Джону фон Нейману удалось создать математическую модель такой машины с довольно сложными правилами — в автомате фон Неймана ячейка может иметь одно из 29-ти состояний, которые эти правила описывают. Конвей поставил целью придумать как можно более простой клеточный автомат с нетривиальным поведением, надеясь, что в таком случае он будет тьюринг-полным. Команда энтузиастов (Конвей, его коллеги и студенты) занималась перебором бесчисленных вариаций правил в поисках подходящих. Итогом стал набор из двух правил для клеток с двумя состояниями, получивших известность как игра «Жизнь». В 1970 году в письме к Мартину Гарднеру Конвей изложил правила и основные сведения о получившейся системе, которые удалось быстро выяснить. Гарднер изложил это в своей колонке о математических играх в журнале Scientific American. Игра «Жизнь» быстро получила тысячи поклонников по всей Америке и за её пределами, а её изобретатель приобрёл известность среди широкой публики[4][5].
Вскоре Конвей доказал тьюринг-полноту игры «Жизнь» (доказательство не было опубликовано). После этого он практически потерял интерес к данной теме.
Конвей был недоволен тем, насколько игра «Жизнь» более известна, чем другие его работы, и не слишком любил о ней рассказывать — кроме как отдельным интересующимся детям[6][7].
Компьютерная реализация[править | править код]

В компьютерных реализациях игры поле ограничено и, как правило, замкнуто — верхняя граница поля «соединена» с нижней, а левая граница — с правой, что представляет собой эмуляцию поверхности тора, но на экране поле всегда отображается в виде равномерной сетки.
Простейший алгоритм «смены поколения» последовательно просматривает все клетки решётки, для каждой подсчитывает соседей, определяя судьбу клетки в новом поколении (не изменится, умрёт, родится). Такой алгоритм использует два двумерных массива — для текущего и для следующего поколений.
Более быстрый алгоритм делает первый проход по всем клеткам, но при этом составляет список клеток для просмотра в последующем поколении. Клетки, которые через поколение принципиально не могут измениться, в список не вносятся. Например, если какая-либо клетка и все её соседи не изменились при текущем обсчёте нового поколения, то эта клетка не изменится и при следующем проходе.
Фигуры[править | править код]
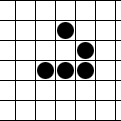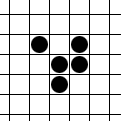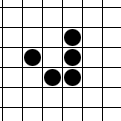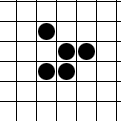

Вскоре после опубликования правил было обнаружено несколько интересных шаблонов (вариантов расстановки живых клеток в первом поколении), в частности: r-пентамино и планер (glider).
Некоторые такие фигуры остаются неизменными во всех последующих поколениях, состояние других периодически повторяется, в некоторых случаях со смещением всей фигуры. Существует фигура (Diehard) всего из семи живых клеток, потомки которой существуют в течение ста тридцати поколений, а затем исчезают.
Конвей первоначально предположил, что никакая начальная комбинация не может привести к неограниченному размножению и предложил премию в 50 долларов тому, кто докажет или опровергнет эту гипотезу. Приз был получен группой из Массачусетского технологического института, придумавшей неподвижную повторяющуюся фигуру, которая периодически создавала движущиеся «планеры». Таким образом, количество живых клеток могло расти неограниченно. Затем были найдены движущиеся фигуры, оставляющие за собой «мусор» из других фигур.
К настоящему времени более-менее сложилась следующая классификация фигур:
- Устойчивые фигуры: фигуры, которые остаются неизменными
- Долгожители: фигуры, которые долго меняются, прежде чем стабилизироваться[8];
- Периодические фигуры: фигуры, у которых состояние повторяется через некоторое число поколений, большее 1;
- Двигающиеся фигуры: фигуры, у которых состояние повторяется, но с некоторым смещением;
- Ружья: фигуры с повторяющимися состояниями, дополнительно создающие движущиеся фигуры;
- Паровозы: двигающиеся фигуры с повторяющимися состояниями, которые оставляют за собой другие фигуры в качестве следов;
- Пожиратели: устойчивые фигуры, которые могут пережить столкновения с некоторыми двигающимися фигурами, уничтожив их;
- Отражатели: устойчивые или периодические фигуры, способные при столкновении с ними движущихся фигур поменять их направление;
- Размножители: конфигурации, количество живых клеток в которых растёт как квадрат количества шагов;
- Фигуры, которые при столкновении с некоторыми фигурами дублируются.
Райский сад[править | править код]

Райским садом (садом Эдема) называется такое расположение клеток, у которого не может быть предыдущего поколения. Практически для любой игры, состояние клеток в которой определяется несколькими соседями на предыдущем шаге, можно доказать существование садов Эдема, но построить конкретную фигуру гораздо сложнее.
«Цифры»[править | править код]
С помощью простейшего «шрифта» размером 3 на 5 клеток, предложенного, по всей видимости, Эриком Анджелини в 2007 году, можно получить очень многие фигуры. Например, число 90, записанное этим шрифтом, порождает планер[9].
Влияние на развитие наук[править | править код]
Хотя игра состоит всего из двух простых правил, тем не менее она более сорока лет привлекает внимание учёных. Игра «Жизнь» и её модификации повлияли (в ряде случаев взаимно) на многие разделы таких точных наук, как математика, информатика и физика[10]. Это, в частности:
- Теория автоматов,
- Теория алгоритмов,
- Теория игр и математическое программирование,
- Алгебра и теория чисел,
- Теория вероятностей и математическая статистика,
- Комбинаторика и теория графов,
- Фрактальная геометрия,
- Вычислительная математика,
- Теория принятия решений,
- Математическое моделирование.
В разделе не хватает ссылок на источники (см. рекомендации по поиску). |
Кроме того, многие закономерности, обнаруженные в игре, имеют свои аналогии в других, подчас совершенно «нематематических» дисциплинах. Вот список наук, теории которых имеют интересные точки соприкосновения с феноменами «Жизни»:
- Кибернетика. Сама игра является удачной попыткой Конвея доказать существование простых самовоспроизводящихся систем, а также появление некоего «разума» у самовоспроизводящихся систем.
- Биология. Внешнее сходство с развитием популяций примитивных организмов впечатляет.
- Бактериология. Некоторые интересные вариации игры с дополнительными условиями могут с точностью повторить размножение бактерий, которые с случайной вероятностью могут мутировать (по условию модификации).
- Физиология. Рождение и смерть клеток подобны процессу возникновения и исчезновения нейронных импульсов.
- Астрономия. Эволюции некоторых сложных колоний удивительным образом схематично повторяют этапы развития спиралевидных галактик[11][12].
- Физика твёрдого тела. Теория автоматов вообще и игра «Жизнь» в частности используются для анализа «явлений переноса» — диффузии, вязкости и теплопроводности.
- Квантовая физика. Поведение «жизненных» ячеек (рождение новых и взаимное уничтожение) во многом напоминают процессы, происходящие при столкновении элементарных частиц.
- Наномеханика. Стационарные и пульсирующие колонии являются показательным примером простейших устройств, созданных на основе нанотехнологий.
- Электротехника. Правила игры используются для моделирования самовосстанавливающихся электрических цепей.
- Химия. Конфигурации, подобные строящимся в игре, возникают во время химических реакций на поверхности; в частности, в опытах М. С. Шакаевой возникают движущиеся молекулярные конструкции, аналогичные «жизненному» планеру. Также предпринимаются попытки объяснить периодические химические реакции с помощью многомерных клеточных автоматов. Самоорганизацией элементарных частиц также занимается супрамолекулярная химия.
Возможно, эта игра связана и с другими научными явлениями, в том числе и с теми, о которых современной науке пока неизвестно. Также возможно, что не открытые на сегодня законы природы и общества станут более понятными благодаря «Жизни» и её модификациям.
Варианты, модификации и обобщения[править | править код]
- Существуют модификации игры «Жизнь» / «Эволюция» по:
- размерности — на плоскости, в объёме;
- цветности — однотоновая, чёрно-белая (шахматная), полноцветная;
- направлению алгоритма — прямой, обратный;
- константам эволюции — классические (B3/S23), изменённые;
- размерам игрового поля — ограниченное, неограниченное, полуограниченное;
- активности поля — активное, пассивное;
- количеству игроков — zero-game, один, два;
- активности игры — пассивная, активная;
- геометрии поля — прямоугольная, шестиугольная.
- Представляет интерес обратная задача Конвея — поиск предшественника заданной фигуры[13]. Для решения её может привлекаться аппарат статистики: метод Монте-Карло, имитационное моделирование, а также весь арсенал эвристических методов.
- Эффективным алгоритмом полноцветной игры является декомпозиция исходного изображения на однотоновые, с последующей, после применения к ним классических правил жизни, их суперпозицией; для объёмных вариантов — ортогональный алгоритм преобразований. Примеры практического применения этого — всевозможные заставки, абстрактные изображения, дизайн произведений искусства.
- В шахматном, чёрно-белом варианте участвуют два игрока, цвет рождения определяется по преобладанию цвета в порождающей триаде, запись ходов осуществляется по правилам шахматных нотаций. Кроме оригинальных граничных образований, здесь наблюдаются коллизии цвета, например, «глайдер» в нотации : белые a2b2c2, чёрные c3b4 — полностью обесцвечивается за цикл преобразований, а то же: белые a2b2, чёрные c2c3 b4 — демонстрируется хроматическая цикличность «глайдера» в рамках его геометрической цикличности.
- В активной шахматной игре игрокам представляется возможность влиять на события «Жизни/Эволюции» единичным введением — выведением ограниченного количества фишек своего цвета с целью экспансии, стабилизации хода истории, противодействия в этом противнику. Теоретические основания здесь — методы принятия решения, аппарат теории игр.
- В трёхмерной реализации игры каждая клетка граничит с 26 другими клетками, выживает при 4-5 соседях, и рождается новая при 5 соседях, а также есть трёхмерные стабильные структуры, некоторые из которых схожи с двухмерными[14].
- В 2018 году Бертом Ван-Чаком было создано семейство клеточных автоматов Lenia как непрерывное обобщение «Игры жизни» Конвея с состояниями непрерывными в пространстве и во времени[15][16][17].
Интересные факты[править | править код]
Этот раздел представляет собой неупорядоченный список разнообразных фактов о предмете статьи. |
- Правила игры таковы, что никакое взаимодействие не может передаваться быстрее хода шахматного короля. Его скорость — одна клетка в любом направлении — часто называют «скоростью света».
- Фигура «планер» в 2003 году была предложена в качестве эмблемы хакеров.
- Первое русскоязычное упоминание «Game of Life» относится к 1971 году и в переводе журнала «Наука и жизнь» известна как «Эволюция».
- Если ввести в строке поиска Google «conway's game of life», то, помимо стандартного результата запроса, как фоновая анимация будет отображаться подобие этой игры[18][19].
- Существуют программы для создания звука из паттернов, сгенерированных в игре «Жизнь», в том числе в MIDI-секвенции[20][21][22][23][неавторитетный источник].
Примечания[править | править код]
- ↑ Gardner, Martin (October 1970). "The fantastic combinations of John Conway's new solitaire game 'life'" (PDF). Mathematical Games. Scientific American. Vol. 223, no. 4. pp. 120—123. doi:10.1038/scientificamerican1070-120. JSTOR 24927642. Архивировано (PDF) из оригинала 9 октября 2022.
- ↑ Berlekamp, E. R. Winning Ways for your Mathematical Plays / E. R. Berlekamp, John Horton Conway, R. K. Guy. — 2nd. — A K Peters Ltd, 2001–2004.
- ↑ Izhikevich, Eugene M.; Conway, John H.; Seth, Anil (2015-06-21). "Game of Life". Scholarpedia (англ.). 10 (6): 1816. Bibcode:2015SchpJ..10.1816I. doi:10.4249/scholarpedia.1816. ISSN 1941-6016.
- ↑ Roberts, 2015, 8. Criteria of Virtue.
- ↑ Martin Gardner. The fantastic combinations of John Conway's new solitaire game "life" // Scientific American. — № 4 (October 1970). Архивировано 27 августа 2013 года.
- ↑ Roberts, 2015, 9. Character Assassination.
- ↑ Joseph O’Rourke. Book Review. Genius at Play: The Curious Mind of John Horton Conway by Siobhan Roberts // The College Mathematics Journal. — 2015. — Vol. 46, no. 4. — P. 309—314. — doi:10.4169/college.math.j.46.4.309.
- ↑ Словарь Жизни: Долгожитель. Дата обращения: 21 сентября 2015. Архивировано 22 сентября 2017 года.
- ↑ Digits in Life. www.radicaleye.com. Дата обращения: 15 июля 2017. Архивировано 8 августа 2017 года.
- ↑ Тоффоли Т., Марголус Н. Машины клеточных автоматов. — М.: Мир, 1991. — ISBN 5-03-001619-8
- ↑ M. W. Mueller, W. D. Arnett. Propagating star formation and irregular structure in spiral galaxies (англ.) // The Astrophysical Journal. — 1976-12-01. — Vol. 210. — P. 670–678. — ISSN 0004-637X. — doi:10.1086/154873.
- ↑ H. Gerola, P. E. Seiden. Stochastic star formation and spiral structure of galaxies (англ.) // The Astrophysical Journal. — 1978-07-01. — Vol. 223. — P. 129–135. — ISSN 0004-637X. — doi:10.1086/156243.
- ↑ Журнал Наука и жизнь. № 8, 1972 г. С. 141—144.
- ↑ Архивированная копия. Дата обращения: 24 августа 2021. Архивировано 18 июля 2021 года.
- ↑ Chan, Bert Wang-Chak (2019-10-15). "Lenia: Biology of Artificial Life". Complex Systems. 28 (3): 251—286. arXiv:1812.05433. doi:10.25088/ComplexSystems.28.3.251.
- ↑ Lenia. chakazul.github.io. Дата обращения: 12 октября 2021.
- ↑ Roberts, Siobhan (2020-12-28). "The Lasting Lessons of John Conway's Game of Life". The New York Times (англ.). ISSN 0362-4331. Дата обращения: 13 октября 2021.
- ↑ Jon Mitchel. How A Google Engineer Built A Universe In An Easter Egg (5 октября 2012). Дата обращения: 31 января 2016. Архивировано 16 октября 2016 года.
- ↑ Siobhan Roberts. Prologue // Genius At Play: The Curious Mind of John Horton Conway. — Bloomsbury Publishing USA, 2015. — P. XV. — 480 p. — ISBN 1-620-40594-6, 978-1-620-40594-9.
- ↑ Burraston, Dave; Edmonds, Ernest; Livingstone, Dan; Miranda, Eduardo Reck (2004). "Cellular Automata in MIDI based Computer Music". Proceedings of the 2004 International Computer Music Conference. CiteSeerX 10.1.1.6.3882. hdl:10453/1425. ISBN 9780971319226.
- ↑ glitchDS – Cellular Automaton Sequencer For The Nintendo DS. Synthtopia.com (29 мая 2008). Дата обращения: 24 июня 2012. Архивировано 26 июля 2012 года.
- ↑ Game Of Life Music Sequencer. Synthtopia.com (29 апреля 2009). Дата обращения: 24 июня 2012. Архивировано 26 июля 2012 года.
- ↑ Game Of Life Music Sequencer For iOS, Runxt Life. Synthtopia.com (12 января 2011). Дата обращения: 24 июня 2012. Архивировано 26 июля 2012 года.
Литература[править | править код]
- Andrew Adamatzky. Game of Life Cellular Automata. — Springer-Verlag London, 2010. — ISBN 978-1-84996-216-2, 978-1-4471-6154-7, 978-1-84996-217-9. — doi:10.1007/978-1-84996-217-9.
- Paul Rendell. Turing Machine Universality of the Game of Life. — Springer International Publishing, 2016. — (Emergence, Complexity and Computation ; vol. 18). — ISBN 978-3-319-19841-5, 978-3-319-19842-2. — doi:10.1007/978-3-319-19842-2.
- Уэзерелл Ч. Этюды для программистов. — М.: Мир, 1982. — С. 19—22.
- Гарднер М. Крестики-нолики. — М.: Мир, 1988. — С. 287—343. — ISBN 5030012346.
- Щеглов Г. Шахматная Эволюция. — Lambert Academic Publishing, 2012. — 88 с. — ISBN 9783848424603.
- Трофимов М. Жизнь на Макинтоше // Монитор, 1995. — № 2, с.72; № 4, с.72; № 5, с.66.
- Журнал Наука и Жизнь. № 8, 1971, с. 130—133.
- Журнал В мире научных открытий. № 5.4(11), 2010, с. 50-53, 139. ISSN 2072-0831 (print), ISSN 2307-9428 (online)
- Приложение к журналу Юный техник. № 8 август 1989, с. 11-13
- Хэйес Б. Клеточный автомат создает модель мира и мир вокруг себя. // В мире науки, 1984, № 5, с.97-104
- Siobhan Roberts. Genius At Play. The Curious Mind of John Horton Conway. — Bloomsbury USA, 2015. — Errata. — ISBN 9781620405932.
Ссылки[править | править код]
- ConwayLife.com — игра «Жизнь» и родственные клеточные автоматы, программа Golly
- Словарь Жизни
- Клумова И. Н. Игра «Жизнь» // Квант. — 1974. — № 9. — С. 26—30.
- Martin Gardner. The fantastic combinations of John Conway's new solitaire game "life" // Scientific American. — Vol. 223, № 4 (October 1970). — P. 120—123. Архивировано 1 мая 2013 года.