Опыт Штерна — Герлаха

Опыт Штерна — Герлаха продемонстрировал, что пространственная ориентация углового момента квантована. Таким образом, было показано, что система атомного масштаба обладает квантовыми свойствами. В первоначальном опыте атомы серебра пропускались через неоднородное магнитное поле, которое отклоняло их до того, как они попадали на экран детектора, например на предметное стекло. Частицы с ненулевым магнитным моментом отклоняются от прямой траектории из-за градиента магнитного поля. Экран показывает дискретные точки на экране, а не непрерывное распределение[1] благодаря их квантованному спину. Исторически этот опыт сыграл решающую роль в убеждении физиков в реальности квантования углового момента во всех системах атомного масштаба[2][3].
Опыт, замысленный Отто Штерном в 1921 году, был впервые успешно проведён Вальтером Герлахом в начале 1922 года[1][4][5].
Описание
[править | править код]Опыт Штерна — Герлаха — опыт, проведённый с пучком атомов серебра, отклоняющихся в неоднородном магнитном поле, который продемонстрировал существование внутренней дискретной степени свободы электронов (спина).
Результаты наблюдений показали, что частицы обладают собственным угловым моментом, который очень похож на угловой момент классически вращающегося объекта, но принимает только определённые квантованные значения. Другой важный результат заключается в том, что одновременно можно измерить только одну составляющую спина частицы, а это означает, что измерение спина по оси z уничтожает информацию о спине частицы по осям x и y.
Опыт обычно проводится с использованием электрически нейтральных частиц, таких как атомы серебра. Это позволяет избежать большого отклонения путей для заряженных частиц, движущихся в магнитном поле, и позволяет измерять преобладающие зависящие от спина эффекты[6][7].
Если рассматривать частицу как классический вращающийся магнитный диполь, она будет прецессировать в магнитном поле из-за крутящего момента, возникающего благодаря действию магнитного поля на диполь (см. прецессию, вызванную крутящим моментом). Если она движется через однородное магнитное поле, силы, действующие на противоположные концы диполя, уравновешивают друг друга, и траектория частицы не изменяется. Однако, если магнитное поле неоднородно, то сила на одном конце диполя будет немного больше, чем противодействующая ей сила на другом конце, так что возникает результирующая сила, которая искривляет траекторию частицы. Если бы частицы были классическими вращающимися объектами, можно было бы ожидать, что распределение их векторов углового момента вращения будет случайным и непрерывным. Каждая частица будет отклоняться на величину, пропорциональную скалярному произведению её магнитного момента на градиент внешнего поля, создавая некоторое распределение плотности на экране детектора. Вместо этого частицы, проходящие через установку Штерна — Герлаха, отклоняются вверх или вниз на определённую величину. Этот результат объясняется измерением квантовой наблюдаемой, теперь известной как спиновой угловой момент, значение которого демонстрируют возможные результаты измерения для наблюдаемой с дискретным набором значений или точечным спектром.
Хотя намного раньше наблюдались некоторые дискретные квантовые явления, такие как атомные спектры, опыт Штерна — Герлаха позволил учёным впервые в истории науки непосредственно наблюдать разделение между дискретными квантовыми состояниями.
Теоретически квантовый угловой момент любого вида имеет дискретный спектр, который иногда кратко выражается как «угловой момент квантуется».
Опыты с частицами с +1⁄2 или −1⁄2 проекциями спина
[править | править код]Если опыт проводится с использованием заряженных частиц, таких как электроны, то на них будет действовать сила Лоренца, стремящаяся направить их траектории по окружности. Эту силу можно скомпенсировать электрическим полем соответствующей величины, ориентированным поперёк траектории заряженной частицы.
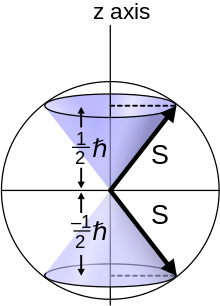
Электроны — частицы со спином 1⁄2. У них есть только два возможных значения спинового углового момента, измеренного вдоль любой оси, или , не имеет классического аналога и является квантовомеханическим проявлением. Поскольку его значение всегда одинаково, оно рассматривается как внутреннее свойство электронов и иногда называется «собственным угловым моментом» (чтобы отличить его от орбитального углового момента, который может варьироваться и зависит от присутствия других частиц). Если измерять проекцию спина вдоль вертикальной оси, состояние электрона описывается как «спин вверх» или «спин вниз» в зависимости от магнитного момента, направленного вверх или вниз соответственно.
Чтобы математически описать опыт для частиц со спином , проще всего использовать обозначение бра и кета Дирака. Когда частицы проходят через установку Штерна — Герлаха, они отклоняются вверх или вниз и наблюдаются детектором, который разрешает либо спин вверх, либо спин вниз. Они описываются квантовым числом углового момента , который принимает одно из двух возможных значений: или . Акт наблюдения (измерения) импульса вдоль оси соответствует оператору . Это математически задаёт начальное состояние частиц равное
где константы и — это комплексные числа. Этот спин в начальном состоянии может указывать в любом направлении. Квадраты абсолютных значений и определяют вероятности того, что система находится после измерения в одном из двух возможных значений начального состояния . Константы и также должны быть нормированы, чтобы вероятность нахождения любого из значений была равна единице, то есть . Однако этой информации недостаточно для определения значений для комплексных чисел и . Поэтому измерение даёт только квадраты этих констант, которые интерпретируются как вероятности.
Последовательные эксперименты
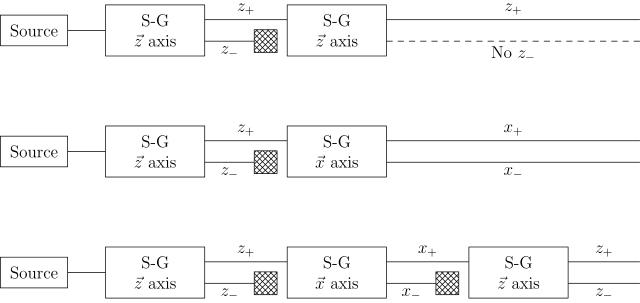
[править | править код]Если поставить несколько установок Штерна — Герлаха последовательно (прямоугольники, содержащие S-G), то становится ясно, что они не действуют как простые селекторы, то есть отфильтровывают частицы с одним из состояний (существовавшим до измерения) и блокируют другие. Вместо этого они изменяют состояние, наблюдая за ним (как при поляризации света). На рисунке ниже x и z обозначают направления (неоднородного) магнитного поля, при этом плоскость xz ортогональна пучку частиц. В трёх показанных ниже системах S-G заштрихованные квадраты обозначают блокировку данного выхода, то есть каждая из установок S-G с блокиратором пропускает в следующую установку S-G последовательно только частицы с одним из двух состояний[8].

Опыт 1
[править | править код]На верхнем рисунке видно, что когда на выходе из первого устройства находится второй идентичный аппарат S-G, на выходе второго устройства видно только z+ . Этот результат ожидается, поскольку ожидается, что все нейтроны в этой точке будут иметь спин z+, поскольку только пучок z+ из первого устройства вошёл во второй аппарат[9].

Опыт 2
[править | править код]Средняя система показывает, что происходит, когда другое устройство S-G размещается на выходе луча z+, полученного в результате прохождения первого аппарата, а второй прибор измеряет отклонение лучей по оси x вместо оси z. Второе устройство выдаёт x+ и x-оси. Теперь в классическом варианте мы ожидаем иметь один луч с характеристикой x, ориентированной на +, и характеристикой z, ориентированной на +, и другой луч с характеристикой x, ориентированной на −, и характеристикой z, ориентированной на +[9].

Опыт 3
[править | править код]Нижняя система противоречит этому ожиданию. Выход третьего устройства, который измеряет отклонение по оси z, снова показывает выход z-, а также z+. Учитывая, что вход во второй аппарат S-G состоял только из z+, можно сделать вывод, что аппарат SG должен изменять состояния частиц, которые проходят через него. Этот опыт можно интерпретировать как демонстрацию принципа неопределённости : поскольку угловой момент не может быть измерен в двух перпендикулярных направлениях одновременно, измерение углового момента в направлении x разрушает предыдущее определение углового момента в направлении z. Вот почему третий прибор измеряет обновлённые лучи z+ и z- так, как измерение x действительно делает чистый лист вывода z+.[9]
История
[править | править код]
Опыт Штерна — Герлаха был задуман Отто Штерном в 1921 году и проведён им совместно с Вальтером Герлахом во Франкфурте в 1922 году[8]. В то время Штерн был ассистентом Макса Борна в Институте теоретической физики Франкфуртского университета и Герлах был ассистентом в Институте экспериментальной физики того же университета.
Во время эксперимента наиболее распространённой моделью описания атома была модель Бора, в которой электроны описывались как движущиеся вокруг положительно заряженного ядра только на определённых дискретных атомных орбиталях или энергетических уровнях. Поскольку энергия электрона квантована так, чтобы он находился только в определённых траекториях в пространстве, разделение на отдельные орбиты называлось квантованием пространства. Эксперимент Штерна — Герлаха должен был проверить гипотезу Бора — Зоммерфельда о том, что направление углового момента атома серебра квантуется[10].
Эксперимент был проведён за несколько лет до того, как Уленбек и Гоудсмит сформулировали свою гипотезу о существовании спина электрона. Несмотря на то, что результат опыта Штерна — Герлаха позже оказался в согласии с предсказаниями квантовой механики для частиц со спином-1⁄2, его следует рассматривать как подтверждение теории Бора — Зоммерфельда[11].
В 1927 году Т. Э. Фиппс и Дж. Б. Тейлор воспроизвели эффект, используя атомы водорода в их основном состоянии, тем самым исключив любые сомнения, которые могли быть вызваны использованием атомов серебра[12]. Однако в 1926 году нерелятивистское уравнение Шрёдингера неверно предсказало, что магнитный момент водорода равен нулю в его основном состоянии. Чтобы решить эту проблему, Вольфганг Паули ввёл «вручную» три матрицы Паули, которые теперь носят его имя, но которые, как позже показал Поль Дирак в 1928 году, являются неотъемлемой частью его релятивистского уравнения.
Сначала эксперимент был проведён с электромагнитом, который позволял постепенно увеличивать неоднородное магнитное поле от нулевого значения[1]. Когда поле было нулевым, атомы серебра осаждались одной полосой на предметном стекле. Когда поле было усилено, середина полосы начала расширяться и, в конце концов, разделилась на две части, так что изображение на предметном стекле выглядело как отпечаток губ с отверстием посередине[13]. В середине, где магнитное поле было достаточно сильным, чтобы разделить луч на две части, статистически половина атомов серебра была отклонена неоднородностью поля.
Значение
[править | править код]Опыт Штерна — Герлаха сильно повлиял на дальнейшее развитие современной физики:
- В последующее десятилетие учёные с помощью аналогичных методов показали, что ядра некоторых атомов также обладают квантованным угловым моментом. Именно взаимодействие этого ядерного углового момента со спином электрона отвечает за сверхтонкую структуру спектроскопических линий[14].
- В 1930-х годах, используя улучшенную версию установки Штерна — Герлаха, Исидор Раби и его коллеги показали, что, используя переменное магнитное поле, можно заставить магнитный момент перейти из одного состояния в другое. Серия экспериментов завершилась в 1937 году, когда они обнаружили, что переходы между состояниями могут быть вызваны использованием изменяющихся во времени полей или радиочастотных полей. Так называемые осцилляции Раби — это рабочий механизм для оборудования магнитно-резонансной томографии, установленного в больницах.
- Позже Норман Ф. Рэмси модифицировал установку Раби, чтобы увеличить время взаимодействия с полем. Чрезвычайная чувствительность из-за частоты излучения делает его очень полезным для точного определения времени, и он до сих пор используется в атомных часах.
- В начале 1960-х годов Рэмси и Даниэль Клеппнер использовали систему Штерна — Герлаха для получения пучка поляризованного водорода в качестве источника энергии для водородного мазера, который до сих пор является одним из самых используемых стандартов частоты.
- Прямое наблюдение за спином является самым прямым свидетельством квантования в квантовой механике.
- Опыт Штерна — Герлаха стал прототипом[15][16][17] для квантового измерения, демонстрируя наблюдение единственного реального значения (собственного значения) изначально неизвестного физического свойства. При входе в магнит установки Штерна — Герлаха направление магнитного момента атома серебра неопределённо, но наблюдается, что он либо параллелен, либо антипараллелен направлению магнитного поля B на выходе из магнита. Атомы с магнитным моментом, параллельным B, были ускорены в этом направлении градиентом магнитного поля; те с антипараллельными моментами ускорялись в противоположном направлении. Таким образом, каждый атом, пересекающий магнит, попадёт на детектор ((5) на диаграмме) только в одно из двух мест. Согласно теории квантовых измерений, волновая функция, представляющая магнитный момент атома, находится в суперпозиции этих двух состояний с различными направлениями магнитного момента, входящих в магнит. Одно собственное значение в направлении спина регистрируется, когда квант импульса передаётся от магнитного поля к атому, вызывая ускорение и смещение в направлении импульса[18].
Примечания
[править | править код]- ↑ 1 2 3 Gerlach, W. (1922). "Der experimentelle Nachweis der Richtungsquantelung im Magnetfeld". Zeitschrift für Physik. 9 (1): 349—352. Bibcode:1922ZPhy....9..349G. doi:10.1007/BF01326983.
- ↑ Experiment in Physics, Appendix 5 // The Stanford Encyclopedia of Philosophy / Edward N. Zalta. — Winter 2016.
- ↑ Friedrich, B. (2003). "Stern and Gerlach: How a Bad Cigar Helped Reorient Atomic Physics". Physics Today. 56 (12). Bibcode:2003PhT....56l..53F. doi:10.1063/1.1650229.
- ↑ Gerlach, W. (1922). "Das magnetische Moment des Silberatoms". Zeitschrift für Physik. 9 (1): 353—355. Bibcode:1922ZPhy....9..353G. doi:10.1007/BF01326984.
- ↑ Gerlach, W. (1922). "Der experimentelle Nachweis des magnetischen Moments des Silberatoms". Zeitschrift für Physik. 8 (1): 110—111. Bibcode:1922ZPhy....8..110G. doi:10.1007/BF01329580. Архивировано 21 апреля 2022. Дата обращения: 5 мая 2022.
- ↑ Mott, N.F., Massey, H.S.W. (1965/1971). The Theory of Atomic Collisions, third edition, Oxford University Press, Oxford UK, pp. 214—219, § 2, Ch. IX, reprinted in Wheeler, J.A. Quantum Theory and Measurement / J.A. Wheeler, W.H. Zurek. — Princeton NJ : Princeton University Press, 1983. — P. 701–706.
- ↑ George H. Rutherford and Rainer Grobe (1997). "Comment on "Stern-Gerlach Effect for Electron Beams"". Phys. Rev. Lett. 81 (4772): 4772. Bibcode:1998PhRvL..81.4772R. doi:10.1103/PhysRevLett.81.4772.
- ↑ 1 2 Sakurai, J.-J. Modern quantum mechanics. — Addison-Wesley, 1985. — ISBN 0-201-53929-2.
- ↑ 1 2 3 Qinxun, Li (June 8, 2020). "Stern Gerlach Experiment:Descriptions and Developments" (PDF). University of Science and Technology of China: 2—5. Дата обращения: 24 ноября 2020.
{{cite journal}}: Википедия:Обслуживание CS1 (url-status) (ссылка) - ↑ Stern, O. (1921). "Ein Weg zur experimentellen Pruefung der Richtungsquantelung im Magnetfeld". Zeitschrift für Physik. 7 (1): 249—253. Bibcode:1921ZPhy....7..249S. doi:10.1007/BF01332793.
- ↑ Weinert, F. (1995). "Wrong theory—right experiment: The significance of the Stern–Gerlach experiments". Studies in History and Philosophy of Modern Physics. 26B (1): 75—86. Bibcode:1995SHPMP..26...75W. doi:10.1016/1355-2198(95)00002-B.
- ↑ Phipps, T.E. (1927). "The Magnetic Moment of the Hydrogen Atom". Physical Review. 29 (2): 309—320. Bibcode:1927PhRv...29..309P. doi:10.1103/PhysRev.29.309.
- ↑ French A. P., Taylor E. F. (1979). An Introduction to Quantum Physics, Van Nostrand Reinhold, London, ISBN 0-442-30770-5, pp. 428—442.
- ↑ Griffiths, David. Introduction to Quantum Mechanics, 2nd ed.. — 2005. — ISBN 0-13-111892-7.
- ↑ Bohm, David. Quantum Theory. — 1951. — P. 326–330.
- ↑ Gottfried, Kurt. Quantum Mechanics. — 1966. — P. 170–174.
- ↑ Eisberg, Robert. Fundamentals of Modern Physics. — 1961. — P. 334–338. — ISBN 0-471-23463-X.
- ↑ Devereux, Michael (2015). "Reduction of the atomic wavefunction in the Stern–Gerlach magnetic field". Canadian Journal of Physics. 93 (11): 1382—1390. Bibcode:2015CaJPh..93.1382D. doi:10.1139/cjp-2015-0031. ISSN 0008-4204.
Статьи Штерна и Герлаха
[править | править код]- Stern, O. Eine direkte Messung der thermischen Molekulargeschwindigkeit. Zeitschrift für Physik, 2:49—56 (1920).
- Gerlach, W. and Stern, O. Der experimentelle Nachweis des magnetischen Moments des Silberatoms. Zeitschrift für Physik, 8:110—111 (1921).
- Gerlach, W. and Stern, O. Der experimentelle Nachweis der Richtungsquantelung im Magnetfeld. Zeitschrift für Physik, 9:349—352 (1922).
- Gerlach, W. and Stern, O. Über die Richtungsquantelung im Magnetfeld. Annalen der Physik, 74:673—699 (1924).
- Gerlach, W. Über die Richtungsquantelung im Magnetfeld II. Annalen der Physik, 76:163—197 (1925).
Литература
[править | править код]- Scully M. O., Shea R., McCullen J. State reduction in quantum mechanics: a calculational example. Physics Reports, 43(13):485—498 (1978).
- Mackintosh A. R. The Stern-Gerlach experiment, electron spin and intermediate quantum mechanics. European Journal of Physics, 4:97—106 (1983).
- Scully M. O., Lamb-Jr. W. E., Barut A. On the Theory of the Stern-Gerlach Apparatus. Foundations of Physics, 17(6):575—583 (1987).
- Platt D. E. A modern analysis of the Stern-Gerlach experiment. American Journal of Physics, 60(4):306—308 (1990).
- Weinert F. Wrong Theory — Right Experiment: The Significance of the Stern-Gerlach Experiments. Studies in the History and Philosophy of Modern Physics, 26(1):75—86 (1995).
- Reinisch G. Stern-Gerlach experiment as the pioneer—and probably the simplest—quantum entanglement test? Physics Letters A, 259:427—430 (1999).
- Friedrich B., Herschbach D. Stern and Gerlach: How a Bad Cigar Helped Reorient Atomic Physics. Physics Today, 56(12):53—59 (2003).
- Friedrich B., Herschbach D. Stern and Gerlach at Frankfurt: Experimental Proof of Space Quantization. In Trageser W., editor, Stern-Stunden. Höhepunkte Frankfurter Physik. Frankfurt: University of Frankfurt, Fachbereich Physik (2005).
- Bernstein J. The Stern-Gerlach Experiment (2010). arXiv:1007.2435
- Sauer T. Multiple Perspectives on the Stern-Gerlach Experiment. In Sauer T. and Scholl R., editors, The Philosophy of Historical Case Studies, pages 251—263: Springer (2016).
- Horst Schmidt-Böcking, Lothar Schmidt, Hans Jürgen Lüdde, Wolfgang Trageser, Tilman Sauer. The Stern-Gerlach Experiment Revisited (англ.). — arXiv:1609.09311.
Ссылки
[править | править код]- Опыт Штерна — Герлаха — статья из Большой советской энциклопедии.
- Элементы большой науки Архивная копия от 27 марта 2008 на Wayback Machine
- Опыт Штерна и Герлаха — научно-популярный фильм, производство Леннаучфильм, 1977 год.












