Центральность

Показатель центральности или близости к центру в теории графов и анализе сетей[англ.] определяет наиболее важные вершины графа. Приложения показателя применяются для выявления наиболее влиятельного лица (лиц) в социальной сети, ключевых узлов инфраструктуры в интернете или городских сетей и разносчиков болезни. Концепции центральности первоначально развивались в анализе социальных сетей и многие термины центральности используются для измерения социологических первоисточников[2]. Не следует путать эти показатели с метриками влияния узлов, которые ищут количественные характеристики влияния каждого узла в сети.
Определение и описание индексов центральности
[править | править код]Индексы центральности являются ответами на вопрос «Что характеризует важность вершины?» Ответ даётся в терминах вещественнозначной функции на вершинах графа, значения которой (как ожидается) обеспечивают ранжирование, которое определяет наиболее важные узлы[3][4][5].
Слово «важность» имеет широкий спектр значений, что приводит ко многим различным определениям центральности. Были предложены две схемы категоризации. «Важность» можно понимать по отношению к типу потока через сеть. Это позволяет центральность классифицировать по типу потока, который считается важным[4]. «Важность» можно альтернативно понимать как участие в целостности в сети. Это позволяет центральности классифицировать на основе того, как они измеряют участие[6]. Оба эти подхода разделяет центральности на различные категории. Центральность, которая пригодна для одной категории, часто будет непригодна, когда применяется к другой категории[4].
Если центральности категорируются по их участию, становится ясным, что большинство центральностей принадлежат одной категории. Число маршрутов, начинающихся из данного узла, отличается только тем, каким образом маршруты определяются и подсчитываются. Ограничение соглашений для этой группы позволяет описание центральностей на спектре маршрутов от длины один (степень связности) до неограниченных мартшрутов (степень влиятельности)[3][7]. Наблюдение, что многие центральности разделяют эти связи, объясняет высокий уровень корреляции между этими индексами.
Описание потоками в сети
[править | править код]Сеть можно считать описанием путей, по которым что-то течёт. Это позволяет описание на основе типов потоков и типов путей, закодированных центральностью. Поток может быть основан на переносах, где каждый неделимый элемент проходит от одного узла в другой подобно доставке пакетов с почтового отделения до дома клиента. Во втором случае есть размножение элемента, который проходит в следующий узел, так что и источник, и цель имеют этот элемент. Примером такого случая является распространение слухов, когда информация распространяется приватно, при этом и источник, и цель информированы в конце процесса. Последним случаем является параллельное размножение, когда элемент размножается по нескольким связям одновременно наподобие трансляции по радио, что обеспечивает одну и ту же информацию многим слушателям одновременно[4].
Аналогично, вид пути можно ограничить до: Геодезических (кратчайшие пути), путей (ни одна вершина не посещается более одного раза, цепей (вершины могут посещаться несколько раз, но ни по одному ребру не проходят дважды) или маршрутов (и вершины, и рёбра могут встретиться несколько раз) [4].
Описание по структуре обходов
[править | править код]Альтернативная классификация может быть получена из способа построения центральности. Это снова приводит к разбиению на два класса — Радиальные или Медианные. Радиальные центральности подсчитывают число маршрутов, которые начинаются/кончаются в данной вершине. Степени связности и степени влиятельности являются примерами радиальных показателей центральности, подсчитывая число маршрутов длины один или неограниченной длины. Медианные центральности подсчитывают маршруты, которые проходят через данную вершину. Каноническим примером является степень посредничества Фримана, число кратчайших маршрутов, которые проходят через данную вершину[6].
Аналогично, подсчёт может захватывать либо объём, либо длину маршрута. Объём — это полное число маршрутов данного типа. Три примера из предыдущего параграфа попадают под эту категорию. Длина — это расстояние от данной вершины до остальных вершин графа. Степень близости к другим узлам Фримана, полное геодезическое расстояние от данной вершины до всех остальных вершин является наиболее известным примером[6]. Заметьте, что эта классификация зависит от типа подсчитываемых маршрутов (то есть маршруты, цепи, пути, геодезические).
Боргатти и Эверетт высказали мнение, что эта типология даёт представление, как сравнивать меры центральности. Центральности, попадающие в ту же самую ячейку в этой 2×2 классификации, достаточно похожи, чтобы быть приемлемыми альтернативами, и можно обоснованно сравнивать, какой показатель лучше для данной задачи. Меры из различных ячеек, однако, абсолютно различны. Любое определение относительной пригодности может происходить только в предопределённом контексте, какая категория более пригодна[6].
Радиально-объёмные центральности, существующие на спектре
[править | править код]Описание путём структуры маршрута показывает, что почти все употребляемые центральности являются радиально-объёмными мерами. Это вселяет веру в то, что вершинная центральность является функцией центральности вершин, с которыми она ассоциирована. Центральности отличаются способом ассоциации.
Боначич показал, что если ассоциация определена в терминах маршрутов, то семейство центральностей можно определить на основе рассматриваемых длин маршрутов[3]. Степень связности подсчитывает число маршрутов длиной единица, степень влиятельности подсчитывает маршруты неограниченной длины. Возможны также альтернативные определения ассоциаций. Альфа-центральность[англ.] позволяет иметь для вершин внешние источники влияния. Центральность Эстрады по подграфам подсчитывает только замкнутые пути (треугольники, четырёхугольники, …).
Сердцем таких мер является наблюдение, что степени матрицы смежности графа дают число маршрутов с длиной, равной степени. Аналогично, экспонента матрицы тесно связана с числом маршрутов заданной длины. Начальное преобразование матрицы смежности позволяет определение подсчёта различных типов маршрутов. При любом подходе центральность вершины можно выразить как бесконечную суммы, либо
для степеней матрицы, либо
для экспонент матрицы, где
- равно длине маршрута,
- является преобразованной матрицей смежности, а
- является компенсирующим параметром, обеспечивающим сходимость суммы.
Семейство мер Боначича не преобразует матрицу смежности. Альфа-центральность[англ.] заменяет матрицу смежности её резольвентой. Центральность подграфа заменяет матрицу смежности её следом. Независимо от начального преобразования матрицы смежности все эти подходы имеют общее ограничивающее поведение. При стремлении к нулю индекс сходится к степени связности. При стремлении к максимальному значению индекс сходится к степени влиятельности[7].
Теоретико-игровая центральность
[править | править код]Общее свойство большинства вышеупомянутых стандартных мер заключается в том, что они оценивают важность узла, фокусируясь только на роли, которую узел играет сам по себе. Однако во многих приложениях такой подход не будет адекватным, поскольку может обнаружиться взаимодействие узлов, если меры применяются к узлам групп.
Например, рассмотрим задачу остановки эпидемии. Просматривая вышеприведённое изображение сети, какие узлы следует вакцинировать? Опираясь на описанные выше меры, мы хотим распознать узлы, которые наиболее важны в распространении болезни. Использование подходов, основанных только на центральностях, которые фокусируются на индивидуальных свойствах узлов, может не быть хорошей идеей. Узлы в красном прямоугольнике по отдельности не могут остановить распространение болезни, но при рассмотрении их как группы мы ясно видим, что они могут остановить болезнь, если она начинается в узлах ,,. Теоретико-игровые центральности пытаются принять во внимание описанные проблемы и возможности, используя средства теории игр. Подход, предложенный в статье Михаляка (с соавторами)[8], использует вектор Шепли. Ввиду сложности вычисления (по времени) вектора Шепли бо́льшая часть усилий в этой области вкладывается в разработку новых алгоритмов и методов, которые опираются на конкретную топологию сети и специальный характер задачи. Такой подход может сократить временну́ю сложность алгоритма с экспоненциальной до полиномиальной.
Важные ограничения
[править | править код]Индексы центральности имеют два важных ограничения, одно ограничение очевидно, другое же едва уловимо. Очевидное ограничение заключается в том, что центральность, которая оптимальна для одного приложения, часто не оптимальна для другого. Более того, если бы это было не так, не нужно бы было столько различных центральностей. Иллюстрацию этого феномена даёт воздушный змей Крэкхарда, для которого три различных понятия центральности дают три различных наиболее центральных вершины[9].
Слабо уловимое ограничение заключается в том, что имеет место повсеместное заблуждение: центральность вершины отражает относительную важность вершин. Индексы центральности разрабатывались явно для ранжирования, что позволяет выделение наиболее важных вершин[3][4]. Они делают это хорошо при упомянутых ограничения. Они не разрабатывались для измерения узлов в общем виде. Недавно физики, работающие в области сетей, начали разрабатывать метрики влияния узлов для решения этой задачи.
Ошибка двояка. Во-первых, ранжирование только по порядку вершин как их важности не отражает разницы в важности между различными уровнями ранжирования. Этот факт можно смягчить путём применения центральности Фримана к рассматриваемой мере центральности, что даёт некоторое понимание важности узлов по их различным количественным показателям центральности. Более того, центральность Фримана позволяет сравнить некоторые сети по показателям из узлов с наибольшим значением[10].
Во-вторых, свойства, которые (правильно) отражают наиболее важные вершины в данной сети/приложении, не обязательно обобщаются на остальные вершины. Для большинства остальных узлов сети ранжирование может оказаться бессмысленным[11][12][13][14]. Это объясняет, например, почему только первые несколько результатов поиска изображения в Google появляются в адекватном порядке. PageRank является крайне нестабильной мерой, показывающей часто противоположный ранг после небольшого изменения параметра поиска[15].
Хотя невозможность обобщения индекса центральности на остальную сеть может показаться на первый взгляд неочевидной, она следует прямо из вышеприведённых определений. Сложные сети имеют неоднородную топологию. В какой степени оптимальная мера зависит от сетевой структуры наиболее важных вершин, в такой степени мера, которая оптимальна для таких вершин, не является оптимальной для остальной сети[11].
Степень связности
[править | править код]Исторически первым и концептуально простейшим понятием является степень связности, которая определяется как число связей, инцидентных узлу (то есть число связей, которое узел имеет). Степень можно интерпретировать в терминах прямого риска узла подхватить что-то проходящее через сеть (таких как вирус или некая информация). В случае ориентированной сети (где связи имеют направление) мы обычно определяем две различные меры степени связности, а именно, полустепень захода и полустепень исхода. Соответственно, полустепень захода — это число связей с узлом, а полустепень исхода — это число связей узла с остальными узлами. Когда связь ассоциируется с некоторым положительным аспектом, таким как дружба или сотрудничество, полустепень захода часто интерпретируется как вид популярности, а полустепень исхода как общительность.
Степень связности вершины для данного графа с вершинами и рёбрами, определяется как
Вычисление степени связности для всех узлов в графе занимает время в представлении графа в виде плотной матрицы смежности, а для рёбер занимает время в представлении с разреженной матрицей.
Определение центральности по уровню узла можно распространить на весь граф и в этом случае мы говорим о центральности графа[10]. Пусть будет узлом с наиболее высокой степенью связности в . Пусть будет связным графом с узлами, который максимизирует следующую величину (с в качестве узла с наибольшей степенью связности в ):
Соответственно, степень центральности графа равна:
Значение максимально, когда граф содержит один центральный узел, с которым соединены все остальные узлы (граф-звезда), и в этом случае
Таким образом, для любого графа
Степень близости к другим узлам
[править | править код]В связном графе нормализованная степень близости узла равна средней длине кратчайшего пути между узлом и всеми другими узлами в графе. Тогда чем центральнее узел, тем ближе он ко все остальным узлам.
Степень близости определил Алекс Бавелас (1950) как обратную величину отдалённости[16][17], то есть
- ,
где равно расстоянию между вершинами и . Однако, когда говорят о степени близости к другим узлам, люди обычно имеют в виду её нормализованную форму, обычно получающуюся из предыдущей формулы путём умножения на , где равно числу узлов в графе. Калибровка позволяет сравнение между узлами графов различного размера.
Рассмотрение расстояния из или во все другие узлы неприменимо для неориентированных графов, тогда как в ориентированных графах они дают совершенно различные результаты. Например, интернет-сайт может иметь высокую степень близости от исходящего соединения, но низкую степень близости от входящих соединений).
Гармоническая центральность
[править | править код]В (необязательно связном) графе гармоническая центральность обращает операции суммирования и обращения в определении степени близости:
- ,
где , если не имеется пути из в . Гармоническую центральность можно нормализовать путём деления на , где равно числу узлов в графе.
Гармоническую центральность предложили Марчиори и Латора (2000)[18], затем независимо Деккер (2005) под именем «значимая центральность»(англ. valued centrality)[19], и Рочат (2009)[20].
Степень посредничества
[править | править код]
Степень посредничества — это мера центральности вершины в графе (существует также степень посредничества ребра, которая здесь не обсуждается). Степень посредничества выражает количественно число раз, когда узел служит мостом в кратчайшем пути между двумя другими узлами. Степень посредничества была введена Линтоном Фриманом как мера количественного выражения взаимодействия человека с другими людьми в социальной сети[21]. В этой концепции вершины, имеющие наибольшую вероятность оказаться на случайно выбранном кратчайшем пути между двумя случайно выбранными вершинами, имеют высокую степень посредничества.
Степень посредничества вершины в графе с вершинами вычисляется следующим образом:
- Для каждой пары вершин (s,t) вычисляются кратчайшие пути между ними.
- Для каждой пары вершин (s,t) определяется доля кратчайших путей, которые проходят через рассматриваемую вершину (здесь, вершину v).
- Суммируем эти доли по всем парам вершин (s,t).
Более компактно степень посредничества можно представить как[22]:
- ,
где равно общему числу кратчайших путей из узла в узел , а равно числу таких путей, которые проходят через . Степень посредничества можно нормализовать путём деления на число пар вершин, не включающих v, что для ориентированных графов равно , а для неориентированных графов равно . Например, в неориентированной звезде центральная вершина (которая содержится в любом возможном кратчайшем пути) имеет степень посредничества (1, если нормализовать), в то время как листья (которые не содержатся ни в одном кратчайшем пути) имеют степень посредничества 0.
С точки зрения вычислений, как степени посредничества, так и степени близости всех вершин графа вовлекают вычисление кратчайших путей между всеми парами вершин графа, что требует время при использовании алгоритма Флойда — Уоршелла. Однако на разреженных графах алгоритм Джонсона может оказаться более эффективным, работая за время . В случае невзвешенных графов вычисления могут быть выполнены с помощью алгоритма Брандеса[22], который затрачивает время . Обычно эти алгоритмы предполагают, что графы не ориентированы и связны с разрешением петель и кратных рёбер. При работе с сетевыми графами, отражающими простые связи, которые часто не имеют петель или кратных рёбер (где рёбра представляют связи между людьми). В этом случае использование алгоритма Брандеса конечный показатель центральности делится на 2, чтобы учесть, что каждый кратчайший путь подсчитывается дважды[22].
Степень влиятельности
[править | править код]Степень влиятельности является мерой влияния узла в сети. Он назначает относительные показатели всем узлам в сети, основываясь на концепции, что связи с узлами с высоким показателем вкладывают больше в показатель рассматриваемого узла, чем такая же связь с узлом с низким показателем[23][5][5]. Показатель PageRank компании Google и центральность узла по Кацу являются вариантами степени влиятельности[24].
Использование матрицы смежности для нахождения степени влиятельности
[править | править код]Для заданного графа с вершинами пусть будет матрицей смежности, то есть , если вершина связана с вершиной , и в противном случае. Относительный показатель центральности вершины можно определить как
- ,
где представляет собой множество соседей вершины , а является константой. После небольших преобразований это выражение можно переписать в векторных обозначениях как уравнение для собственного вектора
В общем случае имеется много различных собственных значений , для которого существует ненулевой собственный вектор. Поскольку элементы матрицы смежности неотрицательны, существует единственное наибольшее собственное значение, которое вещественно и положительно, по теореме Фробениуса — Перрона. Это наибольшее собственное значение даёт желаемую меру центральности[23]. Компонента связанного собственного вектора даёт относительный показатель центральности вершины в сети. Собственный вектор определён с точностью до множителя, так что вполне определено только отношение центральностей вершин. Чтобы определить абсолютное значение показателя, необходимо нормализовать собственный вектор, например, так, что сумма по всем вершинам равна 1 или нормализовать общим числом вершин n. Степенной метод является одним из многих алгоритмов получения собственных значений, который может быть использован для нахождения этого доминирующего собственного вектора[24]. Более того, это может быть обобщено так, что элементы матрицы A могут быть вещественными числами, представляющими силу связи как в стохастической матрице.
Центральность по Кацу
[править | править код]Центральность по Кацу[25] является обобщением степени связности. Степень связности измеряет число прямых соседей, а центральность по Кацу измеряет число всех узлов, которые могут быть связаны путями, при штрафовании дальних узлов. Математически, эта центральность определяется как
- ,
где является множителем ослабления из интервала .
Центральность по Кацу можно рассматривать как вариант степени влиятельности. Другой формой центральности по Кацу является
По сравнению со степенью влиятельности заменяется на
Было показано[26], что главный собственный вектор (соответствующий наибольшему собственному значению матрицы смежности ) является пределом центральности по Кацу при стремлении к снизу.
PageRank
[править | править код]PageRank удовлетворяет следующему равенству
где
равно числу соседей узла (или числу исходящих соединений ориентированного графа). По сравнению со степенью влиятельности и центральностью по Кацу важным отличием является масштабирующий множитель . Отличие PageRank и степени влиятельности заключается в том, что вектор PageRank является левым собственным вектором (то есть собственным вектором транспонированной матрицы, заметьте, что у множителя обратный порядок индексов)[27].
Центральность просачивания
[править | править код]Существует ряд мер центральности для выявления «важности» отдельного узла сложной сети. Однако, они отражают важность узла чисто в топологических терминах и значение узла не зависит никак от «состояния» узла. Значение остаётся постоянным вне зависимости от динамики сети. Это верно даже для мер взвешенного посредничества. Однако узел может быть также центрально расположен в терминах степени посредничества или другой меры центральности, но не быть «центрально расположенным» в контексте сети, в которой имеется просачивание. Просачивание «заразы» происходит в сложных сетях в большом количестве сценариев. Вирусная или бактериальная инфекция может распространяется по социальным сетям людей, известным как сети контактов. Распространение болезни может быть также рассматриваться на высоком уровне абстракции путём рассмотрения сети городов или центров сосредоточения людей, соединённых шоссейными и железными дорогами или авиалиниями. Компьютерные вирусы могут распространяться по компьютерным сетям. Слухи или новости о деловых предложениях и сделках могут также распространяться через социальные сети людей. Во всех этих сценариях «инфекция» распространяется через связи сложной сети, изменяя «состояния» узлов обратимо или необратимо. Например, в эпидемиологическом сценарии индивидуумы переходят от состояния «восприимчивый» к состоянию «заражён». Состояния конкретных узлов по мере распространения «заразы» могут принимать в приведённых выше примерах двоичные значения (такие как «порция новостей получена/не получена»), дискретные значения (восприимчив/заражён/вылечен), или даже непрерывные (такие как пропорция заражённых людей в городе). Общее во всех этих сценариях в том, что распространение «заразы» приводит к изменению состояния узлов сети. Принимая это во внимание, была предложена центральность просачивания (англ. Percolation centrality, PC), которая измеряет важность узла в терминах способствования просачивания через сеть. Эту меру предложили Пайравинан с соавторами[28].
Центральность просачивания определяется для заданного узла и в данное время как пропорция «путей просачивания», которые проходят через узел. «Путь просачивания» — это кратчайший путь между парой узлов, где узел-источник в состоянии просачивания (например, заражён). Целевой узел может находиться в состоянии просачивания, непросачивания или в состоянии частичного просачивания.
- ,
где — полное число кратчайших путей из узла в узел , а — число таких путей, проходящих через . Состояние просачивания узла в момент обозначается как и есть два специальных случая, когда что показывает состояние непротекаемости в момент , и когда , что говорит о полной протекаемости в момент времени . Значения между этими величинами означают частичные состояния просачивания (например, в сети городов это может быть процент заражённых людей в городе).
Веса путей просачивания зависят от уровней просачивания, назначенных исходным узлам, исходя из постулата, что чем выше уровень просачивания исходного узла, тем более важны пути, исходящие из этого узла. Узлы, которые лежат на кратчайших путях, начинающихся в узлах с высоким просачиванием, поэтому потенциально более важны для просачивания. Определение PC можно также расширить, чтобы включить также веса целевых узлов. Вычисление центральности просачивания осуществляется за время при эффективной реализации, позаимствованной к быстрого алгоритма Брандеса, а если при вычислениях требуется учёт весов конечных узлов, время худшего случая равно .
Кросс-кликовая центральность
[править | править код]Кросс-кликовая центральность отдельного узла в сложном графе определяет связи узла с различными кликами. Узел с высокой кросс-кликовой центральностью содействует распространению информации или болезни в графе. Клики — это подграфы, в которых каждый узел соединён со всеми другими узлами клики. Кросс-кликовая центральность узла для данного графа с вершинами и рёбрами обозначается как и равна числу клик, которым вершина принадлежит. Эта мера была использована в статье Фагани[29], но впервые её предложили Эверетт и Боргатти в 1998 под названием «центральность по перекрытию клик».
Центральность Фримана
[править | править код]Центральность любой сети есть мера, насколько централен её наиболее центральный узел по сравнению с другими узлами[10]. Мера центральности тогда (a) вычисляется как сумма разностей центральности между наиболее центральным узлом сети и всеми другими узлами и (b) делится это значение на теоретически наибольшую такую сумму разностей любой сети того же размера[10]. Тогда любая мера центральности может иметь свою собственную меру центральности. Говоря формально, если является мерой центральности точки , если является наибольшей такой мерой в сети и если
является наибольшей суммой разностей в точечной центральности для любого графа с тем же числом узлов, то центральность сети равна[10]
Основанные на различиях меры центральности
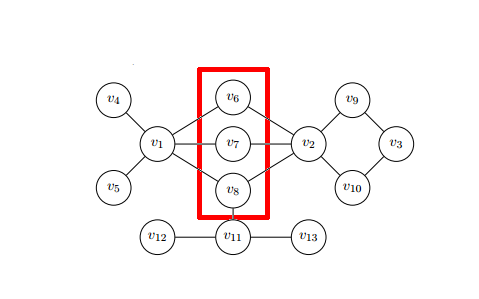
[править | править код]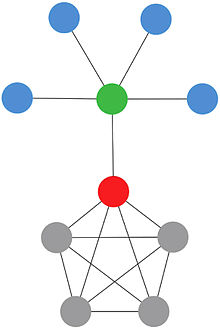
Чтобы получить лучшие результаты в ранжировании узлов данной сети, в статье Алвареза-Сокорро (с соавторами)[30] используется мера непохожести (характерная для теории классификации и анализа данных) для улучшения меры центральности в сложных сетях. Это иллюстрируется степенью влиятельности путём вычисления центральности каждого узла путём решения задачи нахождения собственного значения
- ,
где (покоординатное произведение), а является произвольной матрицей непохожести, определённой через меру непохожести. Например, через непохожесть Жаккара, задаваемую формулой
Эта мера позволяет нам выразить количественно топологический вклад (поэтому и называется центральностью по вкладу) каждого узла в центральность заданного узла, получая большее отношение вес/важность этих узлов с большей непохожестью, поскольку это позволяет заданному узлу достичь узлы, которые не могут быть достигнуты прямо.
Следует обратить внимание, что неотрицательна, поскольку и являются неотрицательными матрицами, так что можем использовать теорему Фробениуса — Перрона, чтобы обеспечить единственность решения задачи выше для с неотрицательным c, что позволяет нам получить центральность каждого узла в сети. Таким образом, центральность i-го узла равна
- ,
где равно числу узлов сети. Некоторые сети и меры непохожести были протестированы в работе Алвареза-Сокорро (с соавторами)[31] и были получены улучшенные результаты в исследуемых случаях.
Обобщения
[править | править код]Эмпирические и теоретические исследования обобщают концепцию центральности в контексте статических сетей на динамические центральности[32] в контексте зависящих от времени и недолговечных сетей[33][34][35].
Для обобщения на взвешенные сети см. статью Опсала с соавторами[36].
Концепция центральности была обобщена также на групповой уровень. Например, степень группового посредничества показывает пропорцию геодезических связей пар (то есть путей с минимальной длиной) узлов, не принадлежащих группе, которые проходят через группу[37][38].
См. также
[править | править код]Примечания
[править | править код]- ↑ Часть терминологии взята из статьи А. С. Семенова и М. В. Бартош «ОЦЕНКА УСТОЙЧИВОСТИ СЕТИ INTERNET OF THINGS С ПОМОЩЬЮ ПОКАЗАТЕЛЕЙ ЦЕНТРАЛЬНОСТИ СВЯЗЕЙ». Термины в литературе на русском языке не устоялись. Так, в статье Евина И. А. Сложные сети: Введение в теорию Архивная копия от 27 января 2018 на Wayback Machine вместо термина «степень посредничества» используются термины «нагрузка узла», «связи с максимальной важностью». На странице Сетевые метрики Архивная копия от 1 июля 2019 на Wayback Machine вместо термина «степень связности» используется буквальный перевод «центральность по степени», вместо терминов «степень …» — «центральность по …». Иногда вместо термина «центральность» используется термин «центрированность»
- ↑ Newman, 2010.
- ↑ 1 2 3 4 Bonacich, 1987, с. 1170–1182.
- ↑ 1 2 3 4 5 6 Borgatti, 2005, с. 55–71.
- ↑ 1 2 3 Negre, Morzan, Hendrickson и др., 2018, с. E12201-E12208.
- ↑ 1 2 3 4 Borgatti, Everett, 2006, с. 466–484.
- ↑ 1 2 Benzi, Klymko, 2013, с. 686–706.
- ↑ Michalak, Aadithya, Szczepański, Ravindran, Jennings, 2013, с. 607—650.
- ↑ Krackhardt, 1990, с. 342–369.
- ↑ 1 2 3 4 5 Freeman, 1979, с. 215–239.
- ↑ 1 2 Lawyer, 2015, с. 8665.
- ↑ da Silva, Viana, da F. Costa, 2012, с. P07005.
- ↑ Bauer, Lizier, 2012, с. 68007.
- ↑ Sikic, Lancic, Antulov-Fantulin, Stefanic, 2013, с. 1–13.
- ↑ Ghoshal, Barabsi, 2011, с. 394.
- ↑ Bavelas, 1950, с. 725–730.
- ↑ Sabidussi, 1966, с. 581–603.
- ↑ Marchiori, Latora, 2000, с. 539–546.
- ↑ Dekker, 2005.
- ↑ Rochat, 2009.
- ↑ Freeman, 1977, с. 35–41.
- ↑ 1 2 3 Brandes, 2001, с. 163–177.
- ↑ 1 2 Newman, 2007, с. 1—12.
- ↑ 1 2 American Mathematical Society. Дата обращения: 18 июня 2019. Архивировано 11 января 2018 года.
- ↑ Katz, 1953, с. 39–43.
- ↑ Bonacich, 1991, с. 155–168.
- ↑ How does Google rank webpages? Архивировано 31 января 2012 года. 20Q: About Networked Life
- ↑ Piraveenan, Prokopenko, Hossain, 2013, с. e53095.
- ↑ Faghani, 2013, с. 1815–1826.
- ↑ Alvarez-Socorro, Herrera-Almarza, González-Díaz, 2015, с. 17095.
- ↑ Alvarez-Socorro A.J., Herrera-Almarza L. A., González-Díaz. Supplementary Information for Eigencentrality based on dissimilarity measures reveals central nodes in complex networks. Nature Publishing Group. Дата обращения: 18 июня 2019. Архивировано 7 марта 2016 года.
- ↑ Braha, Bar-Yam, 2006, с. 59–63.
- ↑ Hill, Braha, 2010, с. 046105.
- ↑ Gross, Sayama, 2009.
- ↑ Holme, Saramäki, 2013.
- ↑ Opsahl, Agneessens, Skvoretz, 2010, с. 245–251.
- ↑ Everett, Borgatti, 2005, с. 57–76.
- ↑ Puzis, Yagil, Elovici, Braha, 2009.
Литература
[править | править код]- Newman M.E.J. Networks: An Introduction. — Oxford, UK: Oxford University Press, 2010.
- Newman M. E. J. The mathematics of networks, // The New Palgrave Encyclopedia of Economics. — Basingstoke,: Palgrave Macmillan, 2007.
- Phillip Bonacich. Power and Centrality: A Family of Measures // American Journal of Sociology. — 1987. — Т. 92, вып. 5. — doi:10.1086/228631.
- Bonacich P. Simultaneous group and individual centralities // Social Networks. — 1991. — Т. 13, вып. 2. — doi:10.1016/0378-8733(91)90018-o.
- Stephen P. Borgatti. Centrality and Network Flow // Social Networks. — 2005. — Т. 27. — doi:10.1016/j.socnet.2004.11.008.
- Christian F. A. Negre, Uriel N. Morzan, Heidi P. Hendrickson, Rhitankar Pal, George P. Lisi, J. Patrick Loria, Ivan Rivalta, Junming Ho, Victor S. Batista. Eigenvector centrality for characterization of protein allosteric pathways // Proceedings of the National Academy of Sciences. — 2018. — Т. 115. — doi:10.1073/pnas.1810452115.
- Stephen P. Borgatti, Martin G. Everett. A Graph-Theoretic Perspective on Centrality // Social Networks. — 2006. — Т. 28, вып. 4. — doi:10.1016/j.socnet.2005.11.005.
- Michele Benzi, Christine Klymko. A matrix analysis of different centrality measures // SIAM Journal on Matrix Analysis and Applications. — 2013. — Т. 36, вып. 2. — doi:10.1137/130950550. — arXiv:1312.6722.
- Tomasz P. Michalak, Karthik V. Aadithya, Piotr L. Szczepański, Balaraman Ravindran, Nicholas R. Jennings. Efficient Computation of the Shapley Valuefor Game-Theoretic Network Centrality // Journal of Artificial Intelligence Research. — 2013. — Т. 46.
- David Krackhardt. Assessing the Political Landscape: Structure, Cognition, and Power in Organizations // Administrative Science Quarterly. — 1990. — Июнь (т. 35, вып. 2). — doi:10.2307/2393394. — .
- Renato da Silva, Matheus Viana, Luciano da F. Costa. Predicting epidemic outbreak from individual features of the spreaders // J. Stat. Mech.: Theory Exp.. — 2012. — Т. 2012. — doi:10.1088/1742-5468/2012/07/p07005. — . — arXiv:1202.0024.
- Frank Bauer, Joseph Lizier. Identifying influential spreaders and efficiently estimating infection numbers in epidemic models: A walk counting approach // Europhys Lett. — 2012. — Т. 99. — С. 68007. — doi:10.1209/0295-5075/99/68007. — . — arXiv:1203.0502.
- Mile Sikic, Alen Lancic, Nino Antulov-Fantulin, Hrvoje Stefanic. Epidemic centrality -- is there an underestimated epidemic impact of network peripheral nodes? // The European Physical Journal B. — 2013. — Т. 86, № 10. — doi:10.1140/epjb/e2013-31025-5. — arXiv:1110.2558.
- Ghoshal G., Barabsi A. L. Ranking stability and super-stable nodes in complex networks. // Nat Commun. — 2011. — Т. 2. — doi:10.1038/ncomms1396. — .
- Glenn Lawyer. Understanding the spreading power of all nodes in a network: a continuous-time perspective // Sci Rep. — 2015. — Т. 5. — doi:10.1038/srep08665. — . — arXiv:1405.6707. — PMID 25727453. — PMC 4345333.
- Linton C. Freeman. Centrality in social networks: Conceptual clarification // Social networks. — 1979. — Т. 1, вып. 3. — С. 215–239. — doi:10.1016/0378-8733(78)90021-7. Архивировано 22 февраля 2016 года.
- Linton Freeman. A set of measures of centrality based upon betweenness // Sociometry. — 1977. — Т. 40, вып. 1. — С. 35–41. — doi:10.2307/3033543. — .
- Alex Bavelas. Communication patterns in task-oriented groups // J. Acoust. Soc. Am. — 1950. — Т. 22, вып. 6.
- Sabidussi G. Sabidussi. The centrality index of a graph // Psychometrika. — 1966. — Т. 31, вып. 4. — doi:10.1007/bf02289527. — PMID 5232444.
- Massimo Marchiori, Vito Latora. Harmony in the small-world // Physica A: Statistical Mechanics and its Applications. — 2000. — Т. 285, вып. 3–4. — doi:10.1016/s0378-4371(00)00311-3. — . — arXiv:cond-mat/0008357.
- Anthony Dekker. Conceptual Distance in Social Network Analysis // Journal of Social Structure. — 2005. — Т. 6, вып. 3.
- Yannick Rochat. Closeness centrality extended to unconnected graphs: The harmonic centrality index // Applications of Social Network Analysis, ASNA 2009. — 2009.
- Ulrik Brandes. A faster algorithm for betweenness centrality // Journal of Mathematical Sociology. — 2001. — Т. 25, вып. 2. — doi:10.1080/0022250x.2001.9990249.
- Newman M. E. J. The mathematics of networks.
- Katz L. A New Status Index Derived from Sociometric Index // Psychometrika. — 1953. — С. 39–43.
- Piraveenan M., Prokopenko M., Hossain L. Percolation Centrality: Quantifying Graph-Theoretic Impact of Nodes during Percolation in Networks // PLOS ONE. — 2013. — Т. 8, вып. 1. — doi:10.1371/journal.pone.0053095. — . — PMID 23349699. — PMC 3551907.
- Mohamamd Reza Faghani. A Study of XSS Worm Propagation and Detection Mechanisms in Online Social Networks // IEEE Transactions on Information Forensics and Security. — 2013. — Т. 8, вып. 11. — doi:10.1109/TIFS.2013.2280884.
- Alvarez-Socorro A. J., Herrera-Almarza G. C., González-Díaz L. A. Eigencentrality based on dissimilarity measures reveals central nodes in complex networks // Scientific Reports. — 2015. — Ноябрь (т. 5). — doi:10.1038/srep17095. — . — PMID 26603652. — PMC 4658528.
- Braha D., Bar-Yam Y. From Centrality to Temporary Fame: Dynamic Centrality in Complex Networks // Complexity. — 2006. — Т. 12, вып. 2. — doi:10.1002/cplx.20156. — . — arXiv:physics/0611295.
- Hill S.A., Braha D. Dynamic Model of Time-Dependent Complex Networks // Physical Review E. — 2010. — Т. 82, вып. 4. — doi:10.1103/physreve.82.046105. — . — arXiv:0901.4407. — PMID 21230343.
- Adaptive Networks: Theory, Models and Applications / Gross T., Sayama H.. — Springer, 2009.
- Holme P., Saramäki J. Temporal Networks. — Springer, 2013.
- Tore Opsahl, Filip Agneessens, John Skvoretz. Node centrality in weighted networks: Generalizing degree and shortest paths // Social Networks. — 2010. — Т. 32, вып. 3. — doi:10.1016/j.socnet.2010.03.006. Архивировано 26 февраля 2018 года.
- Everett M. G., Borgatti S. P. Extending centrality. In P. J. Carrington, J. Scott and S. Wasserman (Eds.) // Models and methods in social network analysis. — New York: Cambridge University Press, 2005. — С. 57–76.
- Puzis R., Yagil D., Elovici Y., Braha D. Collaborative attack on Internet users’ anonymity // Internet Research. — 2009. — Т. 19, вып. 1. Архивировано 7 декабря 2013 года.
Литература для дальнейшего чтения
[править | править код]- Koschützki, D.; Lehmann, K. A.; Peeters, L.; Richter, S.; Tenfelde-Podehl, D. and Zlotowski, O. (2005) Centrality Indices. In Brandes, U. and Erlebach, T. (Eds.) Network Analysis: Methodological Foundations, pp. 16-61, LNCS 3418, Springer-Verlag.
Для улучшения этой статьи желательно:
|





















![{\displaystyle H=\sum _{j=1}^{|Y|}[C_{D}(y*)-C_{D}(y_{j})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9666585dcf8a4913865d385f3e974c6891c879f3)
![{\displaystyle C_{D}(G)={\frac {\sum _{i=1}^{|V|}[C_{D}(v*)-C_{D}(v_{i})]}{H}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29d1d78ee22a5ca4dbfab56ee81d15d2206300f0)



![{\displaystyle C_{D}(G)={\frac {\sum _{i=1}^{|V|}[C_{D}(v*)-C_{D}(v_{i})]}{|V|^{2}-3|V|+2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7551bf124c85cb266574ec4aab363a0f9d6eb05c)








































![{\displaystyle PC^{t}(v)={\frac {1}{N-2}}\sum _{s\neq v\neq r}{\frac {\sigma _{sr}(v)}{\sigma _{sr}}}{\frac {{x^{t}}_{s}}{{\sum {[{x^{t}}_{i}}]}-{x^{t}}_{v}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff9329766cc6f7d93f19d9703dd81488fb14b5e7)























