Циркулянтный граф

Граф Пэли 13-го порядка как пример циркулянтного графа.

Корона с шестью, восемью и десятью вершинами.

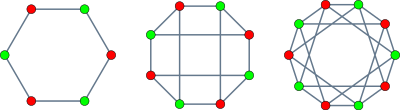
В теории графов циркулянтным графом называется неориентированный граф, имеющий циклическую группу симметрий, которая включает симметрию, переводящую любую вершину в любую другую вершину.

Эквивалентные определения

Циркулянтные графы могут быть определены несколькими эквивалентными способами:

• Автоморфизм группы графа содержит циклическую подгруппу, которая действует транзитивно на вершинах графа.
• Граф имеет матрицу смежности, являющуюся циркулянтом.
• $n$ вершин графа можно пронумеровать числами от 0 до n − 1 таким образом, что если две вершины с номерами $x$ и $y$ смежны, то любые две вершины с номерами $z$ и (z − x + y) mod n тоже смежны.
• Граф можно нарисовать (с возможными пересечениями рёбер) так, что его вершины лежат в углах правильного многоугольника и любой поворот многоугольника в себя является симметрией рисунка (получаем тот же рисунок).

Примеры

Любой цикл является циркулянтным графом, как и любая корона.

Графы Пэли порядка $n$ (где $n$ — простое число, сравнимое с 1 по модулю 4) — это графы, в которых вершины являются числами от 0 до n − 1 и две вершины смежны, если разность соответствующих чисел является квадратичным вычетом по модулю $n$. Вследствие того, что присутствие или отсутствие ребра зависит только от разности номеров вершин по модулю $n$, любой граф Пэли является циркулянтным графом.

Любая лестница Мёбиуса является циркулянтным графом, как и любой полный граф. Полный двудольный граф является циркулянтным, если обе его части имеют одинаковое число вершин.

Если два числа $m$ и $n$ взаимно просты, то m × n ладейный граф (граф, имеющий вершину в каждой клетке шахматной доски m × n и рёбра между любыми двумя клетками, если ладья может перейти с одной клетки на другую за один ход) является циркулянтным графом. Это является следствием того, что его симметрии содержат в качестве подгруппы циклическую группу {{{1}}}. Как обобщение этого случая, прямое произведение графов между любыми циркулянтными графами с $m$ и $n$ вершинами даёт в результате циркулянтный граф.

Многие из известных нижних границ чисел Рамсея появляются из примеров циркулянтных графов, имеющих маленькие максимальные клики и маленькие максимальные независимые множества.

Конкретный пример

Циркулянтный граф $C_{n}^{s_{1},\ldots ,s_{k}}$ (или $C_{n}(s_{1},\ldots ,s_{k})$, или $circ(n:s_{1},\ldots ,s_{k})$) с прыжками $s_{1},\ldots ,s_{k}$ определяется как граф с $n$ узлами, пронумерованными числами $0,1,\ldots ,n-1$ и каждый узел $i$ смежен с 2k узлами $i\pm s_{1},\ldots ,i\pm s_{k}$ по модулю $n$.

• Граф $C_{n}^{s_{1},\ldots ,s_{k}}$ связан тогда и только тогда, когда НОД$(n,s_{1},\ldots ,s_{k})=1$.

• Если $1\leq s_{1}<\cdots <s_{k}$ фиксировнные целые, то число остовных деревьев $t(C_{n}^{s_{1},\ldots ,s_{k}})=na_{n}^{2}$, где $a_{n}$ удовлетворяет рекуррентному соотношению порядка $2^{s_{k}-1}$.
  • В частности, $t(C_{n}^{1,2})=nF_{n}^{2}$, где $F_{n}$ — n-ое число Фибоначчи.

Самодополнительные циркулянты

Самодополнительный граф — это граф, в котором удаление существующих рёбер и добавление отсутствующих даёт граф, изоморфный исходному.

Например, циклический граф с пятью вершинами самодополнителен и является также циркулянтным. В более общем виде, любой граф Пэли является самодополнительным циркулянтным графом. Хорст Сакс показал, что если число $n$ обладает свойством, что любой простой делитель $n$ сравним с 1 по модулю 4, то существует самодополнительный циркулянтный граф с $n$ вершинами. Он высказал гипотезу, что это условие необходимо, то есть при других значениях $n$ самодополнительные циркулянтные графы не существуют. Гипотеза доказана 40 лет позже Вилфредом (Vilfred).

Гипотеза Адамса

Определим циркулянтную нумерацию циркулянтного графа как маркировку вершин графа числами от 0 до n − 1 таким образом, что если две вершины $x$ и $y$ смежны, то любые две вершины с номерами $z$ и (z − x + y) mod n тоже смежны. Эквивалентно, циркулянтная нумерация — это нумерация вершин при которой матрица смежности графа является циркулянтной матрицей.

Пусть $a$ — целое, взаимно простое c $n$, и пусть $b$ — любое целое. Тогда линейная функция ax + b преобразует циркулянтную нумерацию в другую циркулянтную нумерацию. Андраш Адам (András Ádám) высказал гипотезу, что линейное отображение — единственный способ перенумерации вершин графа, сохраняющее свойство циркулянтности. То есть, если $G$ и $H$ — два изоморфных циркулянтных графа с различными нумерациями, то существует линейное преобразование, переводящее нумерацию для $G$ в нумерацию для $H$. Однако, как выяснилось, гипотеза Адама не верна. Контрпримером служат графы $G$ и $H$ с 16-ю вершинами в каждом; вершина $x$ в $G$ соединена с шестью соседями x ± 1, x ± 2, и x ± 7 (по модулю 16), в то время как в $H$ шесть соседей — это x ± 2, x ± 3, и x ± 5 (по модулю 16). Эти два графа изоморфны, но их изоморфизм нельзя получить посредством линейного преобразования.

Ссылки

• Weisstein, Eric W. Circulant Graph (англ.) на сайте Wolfram MathWorld.