Четверная группа Клейна
Четверна́я гру́ппа Кле́йна — нециклическая конечная коммутативная группа четвёртого порядка, играет важную роль в общей алгебре, комбинаторике и геометрии. Обычно обозначается или (от нем. Vierergruppe — четверная группа). Впервые описана и исследована Феликсом Клейном в 1884 году.
-
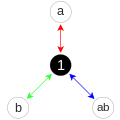
Граф циклов четверной группы Клейна
-
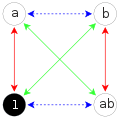
Граф Кэли четверной группы Клейна
Бинарная операция между элементами (единица — нейтральный элемент группы) задаётся следующей таблицей Кэли[1]:
Порядок каждого элемента, отличного от единицы, равен 2, поэтому группа не является циклической. Является прямым произведением циклических групп второго порядка ; наименьшей по порядку нециклической группой.
Является простейшей группой диэдра [2]. Любая группа четвёртого порядка изоморфна либо циклической группе, либо четверной группе Клейна. Симметрическая группа имеет, кроме себя самой и единичной подгруппы, лишь две нормальные подгруппы — знакопеременную группу и четверную группу Клейна , состоящую из подстановок [2].
Встречается во многих разделах математики, примеры изоморфных ей групп:
- множество с операцией побитовое исключающее ИЛИ;
- приведённая система вычетов по модулю 8, состоящая из классов 1, 3, 5, 7 и по модулю 12, состоящая из классов 1, 5, 7, 11;
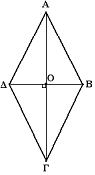
- группа симметрий ромба в трёхмерном пространстве, состоящая из 4 преобразований: тождественное, поворот на и два отражения относительно диагоналей[3].
- группа поворотов тетраэдра на угол вокруг всех трёх рёберных медиан (вместе с тождественным поворотом)[4].
Примечания[править | править код]
- ↑ Александров, 1980, гл. 1 «Понятие группы», п. 2 «Вводные примеры», п. 4 «Клейновская группа четвёртого порядка», с. 23.
- ↑ 1 2 В. Ф. Зайцев. п. 2, Дискретные группы преобразований // Введение в современный групповой анализ. — СПб., 1996. — С. 10.
- ↑ Александров, 1980, гл. 5 «Простейшие группы самосовмещений», п. 3 «Группы поворотов правильной пирамиды и двойной пирамиды», п. 3 «Случай вырождения: группы поворотов отрезка и ромба», с. 71.
- ↑ Александров, 1980, гл. 5 «Простейшие группы самосовмещений», п. 3 «Группы поворотов правильной пирамиды и двойной пирамиды», п. 4 «Группа поворотов правильного тетраэдра», с. 75.
Литература[править | править код]
- П. С. Александров. Введение в теорию групп. — М.: Наука, 1980. — 144 с. с. — (Библиотечка Квант, вып. 7).
- Ф. Клейн. Лекции об икосаэдре и решении уравнений пятой степени. — М.: Наука, 1989. — 336 с.