Вселенная Фридмана
Вселе́нная Фри́дмана (метрика Фридмана — Леметра — Робертсона — Уокера) — одна из космологических моделей, удовлетворяющих полевым уравнениям общей теории относительности (ОТО), первая из нестационарных моделей Вселенной. Получена Александром Фридманом в 1922. Модель Фридмана описывает однородную изотропную в общем случае нестационарную Вселенную с веществом, обладающую положительной, нулевой или отрицательной постоянной кривизной. Эта работа учёного стала первым основным теоретическим развитием ОТО после работ Эйнштейна 1915—1917 гг.
История открытия
[править | править код]Решение Фридмана было опубликовано в авторитетном физическом журнале Zeitschrift für Physik в 1922[1] и 1924 (для Вселенной с отрицательной кривизной)[2]. Решение Фридмана было вначале отрицательно воспринято Эйнштейном (который предполагал стационарность Вселенной и даже ввёл с целью обеспечения стационарности в полевые уравнения ОТО так называемый лямбда-член), однако затем он признал правоту Фридмана. Тем не менее, работы Фридмана (умершего в 1925) остались вначале незамеченными.
Нестационарность Вселенной была подтверждена открытием зависимости красного смещения галактик от расстояния (Эдвин Хаббл, 1929). Независимо от Фридмана, описываемую модель позднее разрабатывали Леметр (1927), Робертсон и Уокер (1935), поэтому решение полевых уравнений Эйнштейна, описывающее однородную изотропную Вселенную с постоянной кривизной, называют моделью Фридмана — Леметра — Робертсона — Уокера.
Эйнштейн не раз подтверждал, что начало теории расширяющейся Вселенной положил А. А. Фридман.
В творчестве А. А. Фридмана работы по теории относительности могли бы на первый взгляд показаться довольно внезапными. Ранее в основном он работал в области теоретической гидромеханики и динамической метеорологии.
Усвоение Фридманом ОТО было весьма интенсивным и в высшей степени плодотворным. Совместно с Фредериксом он взялся за капитальный труд «Основы теории относительности», в которой предполагалось изложить «достаточно строго с логической точки зрения» основы тензорного исчисления, многомерной геометрии, электродинамики, специального и общего принципа относительности.
Книга Фредерикса и Фридмана «Основы теории относительности» — это обстоятельное, подробное изложение теории относительности, основанное на весьма солидном математическом фундаменте геометрии общей линейной связности на многообразии произвольной размерности и теории групп. Исходной для авторов оказывается геометрия пространства-времени.
В 1923 г. была опубликована популярная книга Фридмана «Мир как пространство и время», посвящённая ОТО и ориентированная на довольно подготовленного читателя. В 1924 г. появилась статья Фридмана, рассматривавшая некоторые вырожденные случаи общей линейной связности, которые, в частности, обобщают перенос Вейля и, как считали авторы, «может быть, найдут применение в физике».
И, наконец, главным результатом работы Фридмана в области ОТО стала космологическая нестационарная модель, носящая теперь его имя.
По свидетельству В. А. Фока, в отношении Фридмана к теории относительности преобладал подход математика: «Фридман не раз говорил, что его дело — указать возможные решения уравнений Эйнштейна, а там пусть физики делают с этими решениями, что они хотят»[3].
Изначально, уравнения Фридмана использовали уравнения ОТО с нулевой космологической постоянной. И модели, основанные на них, безоговорочно доминировали (помимо короткого всплеска интереса к другим моделям в 1960-е гг.) вплоть до 1998 года[4]. В тот год вышли две работы, использовавшие в качестве индикаторов расстояния сверхновые типа Ia. В них было убедительно показано, что на больших расстояниях закон Хаббла нарушается и Вселенная расширяется ускоренно, что требует наличия тёмной энергии, известные свойства которой соответствуют Λ-члену.
Современная модель, так называемая «модель ΛCDM», по-прежнему является моделью Фридмана, но уже с учётом как космологической постоянной, так и тёмной материи.
Метрика Фридмана — Робертсона — Уокера
[править | править код]| Вид символов Кристоффеля |
|---|
| Производные выражения от символов Кристоффеля |
Геометрия однородной изотропной Вселенной — это геометрия однородного и изотропного трёхмерного многообразия. Метрикой таких многообразий является метрика Фридмана — Робертсона — Уокера (FWT)[5]:
где χ — так называемое сопутствующие расстояние или конформное, не зависящее от времени, в отличие от масштабного фактора a, t — время в единицах скорости света, s — интервал.
где k принимает значение:
- k = 0 для трёхмерной плоскости,
- k = 1 для трёхмерной сферы,
- k = −1 для трёхмерной гиперсферы,
— трёхмерный радиус-вектор в квазидекартовых координатах.
Существуют всего три типа трёхмерных многообразий: трёхмерная сфера, трёхмерная гиперсфера и трёхмерная плоскость.
Метрика на трёхмерной плоскости даётся простым выражением
Чтоб задать метрику трёхмерной сферы, необходимо ввести 4-мерное евклидово пространство:
и добавить уравнение сферы:
Гиперсферическая метрика уже определяется в 4-мерном пространстве Минковского:
И точно так же, как для сферы, нужно добавить уравнение гиперболоида:
FWT-метрика — не что иное, как сведение всех вариантов воедино и приложение к пространству-времени.
Или в тензорной записи:
где компоненты метрического тензора равны:
где пробегают значения 1…3, , а — временна́я координата.
Основные уравнения
[править | править код]Если же выражение для метрики подставить в уравнения ОТО для идеальной жидкости, то получим следующую систему уравнений:
| Уравнение энергии |
|
|
|---|---|---|
| Уравнение движения |
|
|
| Уравнение неразрывности |
|
|
Запишем полевые уравнения Эйнштейна в следующей форме:
- ,
где Rμν - тензор Риччи:
- ,
a Sμν записывается в терминах энергии импульса:
Т.к. в метрике Фридмана-Робертсона-Уокера все афинные связности с двумя или тремя временными индексами обнуляются, то
- ,
Подставим в ненулевые компоненты тензора Риччи выражения для символов Кристоффеля:
- ,
где - чисто пространственный тензор Риччи:
Из всех тех же соотношений для выбранной метрики:
Тогда, в точке x=0 чисто пространственный тензор Риччи равен:
Но в точке x=0 метрика это просто δij, т.е. в начале координат имеется следующее соотношение двух три-тензоров:
И в силу однородности метрики Фридмана-Робетсона-Уокера это соотношение справедливо при любом преобразовании координат, т.е. соотношение выполняется во всех точках пространства, тогда можно записать:
Компоненты тензора энергии-импульса в нашей метрике будут следующими:
Тогда:
- ,
После подстановки уравнения Эйнштейна примут вид:
Для перехода к уравнениям с Λ-членом необходимо произвести подстановку:
И после элементарных преобразований приходим к итоговому виду.
Уравнение неразрывности следует из условия ковариантного сохранения тензора энергии-импульса:
Полагая здесь ν=0:
Явно запишем ненулевые компоненты тензора энергии-импульса:
подставив эти значения и воспользовавшись выражениями для символов Кристоффеля в FWT-метрике придём к конечному виду уравнения.
где Λ — космологическая постоянная, ρ — средняя плотность Вселенной, P, p — давление, выраженная в Си и естественной системы единиц соответственно, с — скорость света.
Приведённая система уравнений допускает множество решений, в зависимости от выбранных параметров. На самом деле значение параметров фиксированы только на текущий момент и с течением времени эволюционируют, поэтому эволюцию расширения описывает совокупность решений[5].
Объяснение закона Хаббла
[править | править код]Допустим есть источник, расположенный в сопутствующей системе на расстоянии r1 от наблюдателя. Приёмная аппаратура наблюдателя регистрирует фазу приходящей волны. Рассмотрим два интервала времени δt1 и δt2 между точками с одной и той же фазой[5]:
С другой стороны для световой волны в принятой метрике выполняется равенство:
Проинтегрировав это уравнение получим:
Учитывая что в сопутствующих координатах r не зависит от времени, и малость длины волны относительно радиуса кривизны Вселенной, получим соотношение:
Если теперь его подставить в первоначальное соотношение:
Разложим a(t) в ряд Тейлора с центром в точке a(t1) и учтём члены только первого порядка:
После приведения членов и домножения на c:
Соответственно, константа Хаббла:
Следствия
[править | править код]Определение кривизны пространства. Понятие критической плотности
[править | править код]Подставив в уравнение энергии, записанного для текущего момента, выражение для постоянной Хаббла(H0), приведём его к виду:
- ,
где , , ,
плотность вещества и тёмной энергии, отнесённая к критической, сама критическая плотность и вклад кривизны пространства соответственно. Если переписать уравнение следующим образом
- ,
то станет очевидно, что:
Эволюция плотности вещества. Уравнение состояния
[править | править код]| Стадия | Эволюция масштабного фактора |
Параметр Хаббла |
|---|---|---|
| Инфляционная | ||
| Радиационное доминирование p=ρ/3 |
||
| Пылевая стадия p=0 |
||
| -доминирование p=-ρ |
Подставив в уравнение неразрывности уравнение состояния в виде
- (1)
Получим его решение:
Для разных случаев эта зависимость выглядит по-разному:
Случай холодного вещества (например пыль) p = 0
Случай горячего вещества (например излучение) p = ρ/3
Случай энергии вакуума
Благодаря этому, влиянием Ωk на ранних этапах можно пренебречь, то есть считать Вселенную плоской (так как k=0. Одновременно, разная зависимость плотности компонентов от масштабного фактора позволяет выделить различные эпохи, когда расширение определяется только тем или иным компонентом, представленных в таблице.
Также если ввести некую квинтэссенцию из плотности тёмной энергии и плотности барионной и принять, что оно подчиняется выражению (1), то пограничным значением является
При превышении этого параметра расширение замедляется, при меньшем — ускоряется.
Динамика расширения
[править | править код]Λ < 0
Если значение космологической постоянной отрицательно, то действуют только силы притяжения и более никаких. Правая часть уравнения энергии будет неотрицательной только при конечных значениях R. Это означает, что при некотором значении Rc Вселенная начнёт сжиматься при любом значении k и вне зависимости от вида уравнения состояния[8].
Λ = 0
В случае, если космологическая постоянная равна нулю, то эволюция целиком и полностью зависит от начальной плотности вещества[5]:
Если , то расширение продолжается бесконечно долго, в пределе с асимптотически стремящейся к нулю скоростью. Если плотность больше критической, то расширение Вселенной тормозится и сменяется сжатием. Если меньше, то расширение идёт неограниченно долго с ненулевым пределом H.
Λ > 0
Если Λ>0 и k≤0, то Вселенная монотонно расширяется, но в отличие от случая с Λ=0 при больших значениях R скорость расширения растёт[8]:
При k=1 выделенным значением является . В этом случае существует такое значение R, при котором и , то есть Вселенная статична.
При Λ>Λc скорость расширения убывает до какого-то момента, а потом начинает неограниченно возрастать. Если Λ незначительно превышает Λc, то на протяжении некоторого времени скорость расширения остаётся практически неизменной.
В случае Λ<Λc всё зависит от начального значения R, с которого началось расширения. В зависимости от этого значения Вселенная либо будет расширяться до какого-то размера, а потом сожмётся, либо будет неограниченно расширяться.
ΛCDM
[править | править код]| Космологические параметры по данным WMAP и Planck | ||
|---|---|---|
| WMAP[9] | Planck[10] | |
| Возраст Вселенной t0, млрд лет | 13,75±0,13 | 13,81±0,06 |
| Постоянная Хаббла H0, (км/с)/Мпк | 71,0±2,5 | 67,4±1,4 |
| Плотность барионной материи Ωbh2 | 0,0226±0,0006 | 0,0221±0,0003 |
| Плотность тёмной материи Ωсh2 | 0,111±0,006 | 0,120±0,003 |
| Общая плотность Ωt | 1,08+0,09 -0,07 |
1,0±0,02 |
| Плотность барионной материи Ωb | 0,045±0,003 | |
| Плотность тёмной энергии ΩΛ | 0,73±0,03 | 0,69±0,02 |
| Плотность тёмной материи Ωc | 0,22±0,03 | |
ΛCDM — это современная модель расширения, являющаяся моделью Фридмана, включающая в себя помимо барионной материи, тёмную материю и тёмную энергию
Возраст Вселенной
[править | править код]Теоретическое описание
[править | править код]Время с начала расширения, называемая также возрастом Вселенной[11] определяется следующим образом:
С учётом эволюции плотности запишем общую плотность в следующем виде:
Подставив это в уравнение энергии, получим искомое выражение
Наблюдательные подтверждения сводятся к подтверждению самой модели расширения с одной стороны и предсказываемой ею моменты начала различных эпох, а с другой, чтоб возраст самых старых объектов не превышал получающийся из модели расширения возраст всей Вселенной.
Данные наблюдений
[править | править код]Не существует прямых измерений возраста Вселенной, все они измеряются косвенно. Все методы можно разделить на две категории[12]:
- Определение возраста на основе моделей эволюции у самых старых объектов: старых шаровых скоплений и белых карликов.
- В первом случае метод основан на факте, что звезды в шаровом скоплении все одного возраста, опираясь на теорию звёздной эволюции, строятся изохроны на диаграмме «цвет — звёздная величина», то есть кривые равного возраста для звёзд различной массы. Сопоставляя их с наблюдаемым распределением звёзд в скоплении, можно определить его возраст.
- Метод имеет ряд своих трудностей. Пытаясь их решить, разные команды, в разное время получали разные возраста для самых старых скоплений, от ~8 млрд лет[13], до ~ 25 млрд лет[14].
- Белые карлики имеют приблизительно одинаковую массу звёзд-предшественниц, а значит — и приблизительно одинаковую зависимость температуры от времени. Определив по спектру белого карлика его абсолютную звёздную величину на данный момент и зная зависимость время—светимость при остывании, можно определить возраст карлика[15]
- Однако данный подход связан как с большими техническими трудностями, — белые карлики крайне слабые объекты, — необходимо крайне чувствительные инструменты, чтоб их наблюдать. Первым и пока единственным телескопом, на котором возможно решение данной задачи является космический телескоп им. Хаббла. Возраст самого старого скопления по данным группы, работавшей с ним: млрд лет[15], однако, результат оспаривается. Оппоненты указывают, что не были учтены дополнительные источники ошибок, их оценка млрд лет[16].
- Ядерный метод. В его основе лежит тот факт, что разные изотопы имеют разный период полураспада. Определяя текущие концентрации различных изотопов у первичного вещества можно определить возраст элементов в неё входящих.
- Так у звезды CS31082-001, принадлежащей звёздному населению типа II, были обнаружены линии и измерены концентрации тория и урана в атмосфере. Эти два элемента имеют различный период полураспада, поэтому со временем их соотношение меняется, и если как-то оценить первоначальное соотношение обильностей, то можно определить возраст звезды. Оценить можно двояким способом: из теории r-процессов, подтверждённой как лабораторными измерениями, так и наблюдениями Солнца; или можно пересечь кривую изменения концентраций за счёт распада и кривую изменения содержания тория и урана в атмосферах молодых звёзд за счёт химической эволюции Галактики. Оба метода дали схожие результаты: 15,5±3,2[17] млрд лет получены первым способом, [18] млрд лет — вторым.
Виды расстояний.
[править | править код]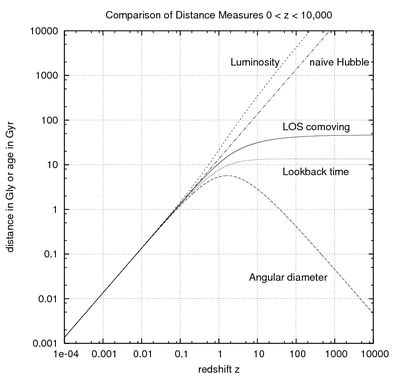
Теоретическое описание
[править | править код]В космологии на больших расстояниях непосредственно измеряемых величин всего три — звёздная величина, характеризующая блеск, угловой размер и красное смещение. Поэтому, для сравнения с наблюдениями вводятся две зависимости:
- Угловой размер от красного смещения, называемого угловым расстоянием:
По определению:
D - собственный размер объекта перпендикулярно к лучу зрения, Δθ - видимый угловой размер. Рассмотрим метрику в сферических координатах:
Размер объекта много меньше расстояния до него, поэтому:
- .
Вследствие малости углового размера dΩ можно принять равным Δθ. Перейдя в метрику текущего момента времени получим конечное выражение
- Блеск от красного смещения — называемого фотометрическим расстоянием:
По определению:
Поток излучения от некоторого источника уменьшается из-за геометрического фактора (), вторым фактором является уменьшение длины фотона в раз и третий фактор - уменьшения частоты прихода отдельных фотонов из-за растяжения времени, также в раз. В итоге получаем для интегрального потока:
После чего путём простых преобразований получаем исходный вид
Также в научно-популярной литературе можно встретить ещё три вида расстояний: расстояние между объектами на текущей момент, расстояние между объектами на момент испускания принятого нами света и расстояние, которое прошёл свет.
Данные наблюдений
[править | править код]Этот раздел не завершён. |
Для измерения фотометрического расстояния необходим источник известной светимости, так называемая стандартная свеча. Для космологических масштабов в качестве таковой берутся сверхновые типа Ia. Они возникают как следствие термоядерного взрыва белого карлика приблизившегося к пределу Чандрасекара.
Сфера Хаббла. Горизонт частиц. Горизонт событий
[править | править код]Также преимущественно в научно-популярной литературе используется термин «сфера Хаббла» — это сфера, чей радиус равен расстоянию, при котором скорость убегания равна скорости света[19][20].
См. также
[править | править код]- Большой взрыв
- Жорж Леметр
- Решения уравнений Эйнштейна
- Уравнение Фридмана (геофизическая гидродинамика)
- Уравнение Фридмана
Примечания
[править | править код]- ↑ Friedmann, A: Über die Krümmung des Raumes (О кривизне пространства), Z. Phys. 10 (1922) 377—386.
- ↑ Friedmann, A: Über die Möglichkeit einer Welt mit konstanter negativer Krümmung des Raumes (О возможности Вселенной с постоянной отрицательной кривизной пространства), Z. Phys. 21 (1924) 326—332.
- ↑ Фок В.А. Работы А. А. Фридмана по теории тяготения Эйнштейна // Успехи физических наук : журнал. — Российская академия наук, 1963. — Т. LXXX, № 3. — С. 353—356. Архивировано 18 июля 2018 года.
- ↑ О непопулярности моделей с космологической постоянной красноречиво говорит тот факт, что Вайнберг в своей книге «Космология и гравитация» (на русском языке издана в 1975 году) параграф о моделях с космологической постоянной относит в раздел вместе с наивными моделями и моделями стационарной Вселенной, отводя на описание 4 страницы из 675.
- ↑ 1 2 3 4
- А. В. Засов., К. А. Постнов. Общая астрофизика. — Фрязино: Век 2, 2006. — С. 421—432. — 496 с. — ISBN 5-85099-169-7.
- Д. С. Горбунов, В. А. Рубаков. Введение в теорию ранней Вселенной: Теория горячего Большого взрыва. — Москва: ЛКИ, 2008. — С. 45—80. — 552 с. — ISBN 978-5-382-00657-4.
- Стивен Вайнберг. Космология. — Москва: УРСС, 2013. — С. 21—81. — 608 с. — ISBN 978-5-453-00040-1.
- ↑ Стивен Вайнберг. Космология. — Москва: УРСС, 2013. — С. 57—59. — 608 с. — ISBN 978-5-453-00040-1.
- ↑ Д.С. Горбунов, В.А. Рубаков. Введение в теорию ранней Вселенной: Теория горячего Большого взрыва. — Москва: ЛКИ, 2008. — С. 63. — 552 с. — ISBN 978-5-382-00657-4.
- ↑ 1 2 Майкл Роуэн-Робинсон. Космология = Cosmology / Перевод с английского Н.А. Зубченко. Под научной редакцией П.К. Силаева. — М.-Ижевск: НИЦ «Регулярная и хаотическая динамика», 2008. — С. 96—102. — 256 с. — ISBN 976-5-93972-659-7.
- ↑ Jarosik, N., et.al. (WMAP Collaboration). Seven-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Sky Maps, Systematic Errors, and Basic Results (PDF). nasa.gov. Дата обращения: 4 декабря 2010. Архивировано 16 августа 2012 года. (from NASA’s WMAP Documents Архивная копия от 30 ноября 2010 на Wayback Machine page)
- ↑ Planck Collaboration. Planck 2013 results. XVI. Cosmological parameters. — arXiv:1303.5076.
- ↑ Астронет > Вселенная. Дата обращения: 27 мая 2015. Архивировано 27 мая 2015 года.
- ↑ Donald D. Clayton. COSMOLOGY, COSMOCHRONOLOGY.
- ↑ Gratton Raffaele G., Fusi Pecci Flavio, Carretta Eugenio и др. Ages of Globular Clusters from HIPPARCOS Parallaxes of Local Subdwarfs. — Astrophysical Journal, 1997.
- ↑ Peterson Charles J. Ages of globular clusters. — Astronomical Society of the Pacific, 1987.
- ↑ 1 2 Harvey B. Richer et al. Hubble Space Telescope Observations of White Dwarfs in the Globular Cluster M4. — Astrophysical Journal Letters, 1995.
- ↑ Moehler S, Bono G. White Dwarfs in Globular Clusters. — 2008. Архивировано 6 августа 2017 года.
- ↑ Schatz Hendrik, Toenjes Ralf, Pfeiffer Bernd. Thorium and Uranium Chronometers Applied to CS 31082-001. — The Astrophysical Journal, 2002.
- ↑ N. Dauphas. URANIUM-THORIUM COSMOCHRONOLOGY. — 2005. Архивировано 19 мая 2014 года.
- ↑ Сергей Попов. Сверхсветовое разбегание галактик и горизонты Вселенной: путаница в тонкостях. Дата обращения: 10 июля 2015. Архивировано 10 ноября 2014 года.
- ↑ TM Davis & CH Linewater. Expanding Confusion: common misconceptions of cosmological horizons and the superluminal expansion of the universe. — 2003. — arXiv:astro-ph/0310808.
Ссылки
[править | править код]- Harrison, E. R. (1967), "Classification of uniform cosmological models", Monthly Notices of the Royal Astronomical Society, 137: 69—79, Bibcode:1967MNRAS.137...69H, doi:10.1093/mnras/137.1.69
- D'Inverno, Ray (1992), Introducing Einstein's Relativity, Oxford: Oxford University Press, ISBN 978-0-19-859686-8
























![{\displaystyle R_{ij}={\frac {\partial \Gamma _{ki}^{k}}{\partial x^{j}}}-\left[{\frac {\partial \Gamma _{ij}^{k}}{\partial x^{k}}}+{\frac {\partial \Gamma _{ij}^{0}}{\partial t}}\right]+\Gamma _{ik}^{0}\Gamma _{j0}^{k}+\Gamma _{i0}^{k}\Gamma _{jk}^{0}+\Gamma _{ik}^{l}\Gamma _{jl}^{k}-(\Gamma _{ij}^{k}\Gamma _{kl}^{l}+\Gamma _{ij}^{0}\Gamma _{0l}^{l})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3168e3c16a7d82bbbe468315326e8836c4efce8f)




















































![{\displaystyle R\propto exp[(\Lambda /3)^{1/2}t].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce434c9fff9e6018a4fe3558f05f19a069c55229)
















