Быстрый обратный квадратный корень

Бы́стрый обра́тный квадра́тный ко́рень (также быстрый InvSqrt() или 0x5F3759DF по используемой «магической» константе) — это приближённый алгоритм вычисления обратного квадратного корня для положительных 32-битных чисел с плавающей запятой. Алгоритм использует целочисленные операции «вычесть» и «битовый сдвиг», а также дробные «вычесть» и «умножить» — без медленных операций «разделить» и «квадратный корень». Несмотря на «хакерство» на битовом уровне, приближение монотонно и непрерывно: близкие аргументы дают близкий результат. Точности (менее 0,2 % в меньшую сторону и никогда — в большую)[1][2] не хватает для настоящих численных расчётов и даже для нормирования матриц поворота в трёхмерной графике[3], однако вполне достаточно для маловажных эффектов вроде освещения и теней.
Алгоритм[править | править код]
Алгоритм принимает 32-битное число с плавающей запятой (одинарной точности в формате IEEE 754) в качестве исходных данных и производит над ним следующие операции:
- Трактуя 32-битное дробное число как целое, провести операцию y0 = 5F3759DF16 − (x >> 1), где >> — битовый сдвиг вправо. Результат снова трактуется как 32-битное дробное число.
- Для уточнения можно провести одну итерацию метода Ньютона: y1 = y0(1,5 − 0,5xy0²).
Реализация из Quake III[4]:
float Q_rsqrt( float number )
{
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
i = * ( long * ) &y; // evil floating point bit level hacking
i = 0x5f3759df - ( i >> 1 ); // what the fuck?
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
return y;
}
Эта реализация считает, что float по длине равен long, и использует для преобразования указатели (может ошибочно сработать оптимизация «если изменился float, ни один long не менялся»; на GCC при компиляции в «выпуск» срабатывает предупреждение). По комментариям видно, что Джон Кармак, выкладывая игру в открытый доступ, не понял, что там делается, и использовал нецензурное выражение (в переводе с англ. — «Что за херня?»).
Корректная по меркам современного Си реализация, с учётом возможных оптимизаций и кроссплатформенности:
#include <stdint.h>
float Q_rsqrt( float number )
{
const float x2 = number * 0.5F;
const float threehalfs = 1.5F;
union {
float f;
uint32_t i;
} conv = {number}; // member 'f' set to value of 'number'.
conv.i = 0x5f3759df - ( conv.i >> 1 );
conv.f *= threehalfs - x2 * conv.f * conv.f;
return conv.f;
}
На Си++20 можно использовать новую функцию bit_cast.
#include <bit>
#include <limits>
#include <cstdint>
constexpr float Q_rsqrt(float number) noexcept
{
static_assert(std::numeric_limits<float>::is_iec559); // Проверка совместимости целевой машины
float const y = std::bit_cast<float>(
0x5f3759df - (std::bit_cast<std::uint32_t>(number) >> 1));
return y * (1.5f - (number * 0.5f * y * y));
}
GCC и Clang (-std=c++20 -mx32 -O3) дают одинаковый машинный код для всех трёх вариантов и близкий — друг относительно друга. У MSVC (/std:c++20 /O2) третья функция незначительно отличается от первых двух.
История[править | править код]
Саму идею приближения дробного числа целым для вычисления придумали Уильям Кэхэн и К. Ын в 1986[5]. До этой идеи добрались Грег Уолш, Клив Моулер и Гэри Таролли, работавшие тогда в Ardent Computer[6][7]. Грегу Уолшу и приписывается знаменитая константа 0x5F3759DF.
Таролли, перешедший в 3dfx, принёс алгоритм туда, где он и применялся для расчёта углов падения и отражения света в трёхмерной графике. Джим Блинн, специалист по 3D-графике, переизобрёл метод в 1997 году с более простой константой 1,5[8]. Более сложный табличный метод, который считает до 4 знаков (0,01 %), найден при дизассемблировании игры Interstate ’76 (1997)[9].
Однако данный метод не появлялся на общедоступных форумах, таких как Usenet, до 2002—2003-х годов. Метод обнаружили в Quake III: Arena, опубликованном в 2005, и приписали авторство Джону Кармаку. Тот предположил, что его в id Software принёс Майкл Абраш, специалист по графике, или Терье Матисен, специалист по ассемблеру; другие ссылались на Брайана Хука, выходца из 3dfx[10]. Изучение вопроса показало, что код имел более глубокие корни как в аппаратной, так и в программной сферах компьютерной графики. Исправления и изменения производились как Silicon Graphics, так и 3dfx Interactive, при этом самая ранняя известная версия написана Гэри Таролли для SGI Indigo.
С выходом в свет в 1998 году набора инструкций 3DNow! в процессорах фирмы AMD появилась ассемблерная инструкция PFRSQRT[11] для быстрого приближенного вычисления обратного квадратного корня. Версия для double бессмысленна — точность вычислений не увеличится[2] — потому её не добавили. В 2000 году в SSE2 добавили функцию RSQRTSS[12] более точную, чем данный алгоритм (0,04 % против 0,2 %). Потому данный метод больше не имеет смысла в современных компьютерах[13] (все x64-процессоры поддерживают SSE2, и все настольные видеоускорители поддерживают Transform & Lighting), зато важен как дань истории и в более ограниченных машинах[14].
Анализ и погрешность[править | править код]
Преобразование «дробное ↔ целое»[править | править код]
Битовое представление 4-байтового дробного числа в формате IEEE 754 выглядит так:
| Знак | ||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Порядок | Мантисса | |||||||||||||||||||||||||||||||
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 31 | 24 | 23 | 16 | 15 | 8 | 7 | 0 | |||||||||||||||||||||||||
Имеем дело только с положительными числами (знаковый бит равен нулю), не денормализованными, не ∞ и не NaN. Такие числа в стандартном виде записываются как 1,mmmm2·2e. Часть 1,mmmm называется мантиссой, e — порядком. Головную единицу не хранят (неявная единица), так что величину 0,mmmm назовём явной частью мантиссы. Кроме того, у машинных дробных чисел смещённый порядок: 20 записывается как 011.1111.12[a].
На положительных числах биекция «дробное ↔ целое» (ниже обозначенная как ) непрерывна как кусочно-линейная функция и монотонна. Отсюда сразу же можно заявить, что быстрый обратный корень, как комбинация непрерывных функций, непрерывен. А первая его часть — сдвиг-вычитание — к тому же монотонна и кусочно-линейна. Биекция сложна, но почти «бесплатна»: в зависимости от архитектуры процессора и соглашений вызова, нужно или ничего не делать, или переместить число из дробного регистра в целочисленный.
В примере выше целочисленное представление равняется 0x3E20.0000, и оно раскладывается так: знаковое поле 0, смещённый порядок[a] 011.1110.02=124, несмещённый 124−127=−3, мантисса (вместе с неявной единицей) 1,012=1,25, и дробное значение 1,25·2−3=0,15625.
Обозначим явную часть мантиссы числа , — несмещённый порядок, — разрядность мантиссы, — смещение порядка. Число[b] будет иметь целочисленное представление . Можно выписать и обратное преобразование: , , ведь первое целое, а второе от 0 до 1.
Первое приближение[править | править код]
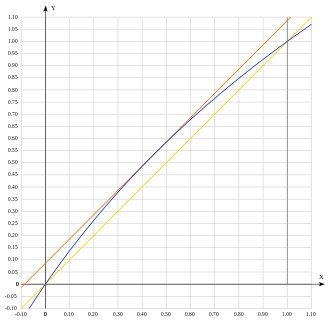
Поскольку и , нелинейную функцию «логарифм» можно приблизить линейной , где — параметр, используемый для настройки точности приближения. Этот параметр варьируется от 0 (формула точна при и ) до 0,086 (точна в одной точке, ).
Аргумент , записанный в линейно-логарифмической разрядной сетке компьютерных дробных, можно[4][15] приблизить логарифмической сеткой как . Перегруппируем , тогда целочисленное представление числа можно приблизить как
Соответственно, . 1️⃣
Проделаем это же[4] для (соответственно )
- 2️⃣
Соединив 1️⃣ и 2️⃣, получаем[4]
Это и есть формула первого приближения.
Магическая константа Q[править | править код]
Магическая константа находится в пространстве компьютерных целых, но её дробное представление также важно для исследователей. Его несмещённый порядок
- .
Поскольку , то независимо от чётности числа B
Смещение порядка B нечётное, и полная мантисса числа равняется
- ),
а в двоичной записи[a] — 0|101.1111.0|011… (1 — неявная единица; 0,5 пришли из порядка; маленькая единица соответствует диапазону [1,375; 1,5) и потому крайне вероятна, но не гарантирована нашими прикидочными расчётами.)

Через константу c можно вычислить, чему равняется первое кусочно-линейное приближение[16] (в источнике используется не сама мантисса, а её явная часть ):
- Для : ;
- Для : ;
- Для : .
На бо́льших или меньших результат пропорционально меняется: при учетверении результат уменьшается ровно вдвое.
Метод Ньютона[править | править код]
Метод Ньютона даёт[16] , , и . Функция убывает и выпукла вниз, на таких функциях метод Ньютона подбирается к истинному значению слева — потому алгоритм всегда занижает ответ.
После одного шага метода Ньютона результат получается довольно точный (+0 % −0,18 %)[1][2], что для целей компьютерной графики более чем подходит (1⁄256 ≈ 0,39 %). Такая погрешность сохраняется на всём диапазоне нормированных дробных чисел. Два шага дают точность в 5 цифр[1], после четырёх достигается погрешность double.
Метод Ньютона не гарантирует монотонности, но компьютерный перебор показывает, что монотонность всё-таки есть.
#include <iostream>
union FloatInt {
float asFloat;
int32_t asInt;
};
int floatToInt(float x)
{
FloatInt r;
r.asFloat = x;
return r.asInt;
}
float intToFloat(int x)
{
FloatInt r;
r.asInt = x;
return r.asFloat;
}
float Q_rsqrt( float number )
{
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
i = * ( long * ) &y; // evil floating point bit level hacking
i = 0x5f3759df - ( i >> 1 ); // what the fuck?
y = * ( float * ) &i; // i don't know, what the fuck!
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
return y;
}
int main()
{
int iStart = floatToInt(1.0);
int iEnd = floatToInt(4.0);
std::cout << "Numbers to go: " << iEnd - iStart << std::endl;
int nProblems = 0;
float oldResult = std::numeric_limits<float>::infinity();
for (int i = iStart; i <= iEnd; ++i) {
float x = intToFloat(i);
float result = Q_rsqrt(x);
if (result > oldResult) {
std::cout << "Found a problem on " << x << std::endl;
++nProblems;
}
}
std::cout << "Total problems: " << nProblems << std::endl;
return 0;
}
Существуют аналогичные алгоритмы для других степеней, например, квадратного или кубического корня[4].
Мотивация[править | править код]

«Прямое» наложение освещения на трёхмерную модель, даже высокополигональную, даже с учётом закона Ламберта и других формул отражения и рассеивания, сразу же выдаст полигональный вид — зритель увидит разницу в освещении по рёбрам многогранника[17]. Иногда так и нужно — если предмет действительно угловатый. А для криволинейных предметов поступают так: в трёхмерной программе указывают, острое ребро или сглаженное[17]. В зависимости от этого ещё при экспорте модели в игру по углам треугольников вычисляют нормаль единичной длины к криволинейной поверхности. При анимации и поворотах игра преобразует эти нормали вместе с остальными трёхмерными данными; при наложении освещения — интерполирует по всему треугольнику и нормализует (доводит до единичной длины).
Чтобы нормализовать вектор, надо разделить все три его компонента на длину. Или, что лучше, умножить их на величину, обратную длине: . За секунду должны вычисляться миллионы этих корней. До того как было создано специальное аппаратное обеспечение для обработки трансформаций и освещения, программное обеспечение вычислений могло быть медленным. В частности, в начале 1990-х, когда код был разработан, большинство вычислений с плавающей запятой отставало по производительности от операций с целыми числами.
Quake III Arena использует алгоритм быстрого обратного квадратного корня для ускорения обработки графики центральным процессором, но с тех пор алгоритм уже был реализован в некоторых специализированных аппаратных вершинных шейдерах, используя специальные программируемые матрицы (FPGA).
Даже на компьютерах 2010-х годов, в зависимости от загрузки дробного сопроцессора, скорость может быть втрое-вчетверо выше, чем с использованием стандартных функций[16].
Дальнейшие улучшения[править | править код]
При желании можно перебалансировать погрешность, умножив коэффициенты 1,5 и 0,5 на 1,0009, чтобы метод давал симметрично ±0,09 % — так поступили[9] в игре Interstate ’76, которая также делает итерацию метода Ньютона.
Константа Уолша 0x5F3759DF ↔[c] 1,4324301·263 оказалась очень хорошей. Крис Ломонт и Мэттью Робертсон незначительно уменьшили[1][2] предельную относительную погрешность, отыскав перебором константу[d] 0x5F375A86 ↔ 1,4324500·263, а для double — 0x5FE6EB50C7B537A9. Правда, для double алгоритм бессмысленный (не даёт выигрыша в точности по сравнению с float)[2]. Константу Ломонта удалось получить и аналитически (c = 1,432450084790142642179)[d], но расчёты довольно сложны[2][16]. Крайний случай — константа Блинна 1,5 — даёт без перебалансировок и улучшений около −0,6 %[8].
Чех Ян Ка́длец двоичным поиском, а затем перебором в окрестности найденного улучшил алгоритм[18]. Его метод даёт в 1,3 раза меньшую симметричную погрешность — не ±0,09 %, а ±0,065.
float inv_sqrt(float x)
{ union { float f; uint32 u; } y = {x};
y.u = 0x5F1FFFF9ul - (y.u >> 1);
return 0.703952253f * y.f * (2.38924456f - x * y.f * y.f);
}
Вместо метода Ньютона можно использовать метод Галлея, в данной задаче эквивалентный методу Ньютона для уравнения . Он точнее одного шага метода Ньютона, но не дотягивает до двух и требует деление[18]:
где нужно рассчитать всего один раз и сохранить во временной переменой.
Предложено необычное улучшение нулевого (без метода Ньютона) приближения: вычислить два обратных корня четвёртой степени с разными константами и перемножить их как дробные[3].
Комментарии[править | править код]
- ↑ 1 2 3 Здесь и далее точки — границы полубайтов, вертикальные линии — границы полей компьютерного дробного.
- ↑ Здесь и далее ≡ означает «равно по определению».
- ↑ Здесь стрелка ↔ означает объяснённую выше биекцию двоичного представления целого числа и двоичного представления числа с плавающей запятой в формате IEEE 754.
- ↑ 1 2 Если в поле порядка поставить 127, получится 0x3FB75A86. Библиотека GRISU2, полностью целочисленная и не зависящая от тонкостей сопроцессора, говорит, что 0x3FB75A86 ↔ 1,43245 — это кратчайшее десятичное число, преобразующееся в данный float. Однако всё-таки единица младшего разряда равняется 1,19·10−7, и 0x3FB75A86 = 1,432450056 ≈ 1,4324501. Следующее дробное 0x3FB75A87 ↔ 1,4324502 без всяких тонкостей. Отсюда неинтуитивное округление 1,43245008 до 1,4324500.
Примечания[править | править код]
- ↑ 1 2 3 4 Архивированная копия. Дата обращения: 25 августа 2019. Архивировано 6 февраля 2009 года.
- ↑ 1 2 3 4 5 6 https://web.archive.org/web/20140202234227/http://shelfflag.com/rsqrt.pdf
- ↑ 1 2 The Truth about the Fast Inverse Square Root on the N64 - YouTube. Дата обращения: 21 ноября 2023. Архивировано 21 ноября 2023 года.
- ↑ 1 2 3 4 5 Hummus and Magnets. Дата обращения: 1 февраля 2017. Архивировано 13 января 2017 года.
- ↑ Источник. Дата обращения: 9 апреля 2023. Архивировано 13 апреля 2023 года.
- ↑ Beyond3D — Origin of Quake3’s Fast InvSqrt() — Part Two. Дата обращения: 25 августа 2019. Архивировано 25 августа 2019 года.
- ↑ Symplectic Spacewar » Cleve’s Corner: Cleve Moler on Mathematics and Computing - MATLAB & Simulink. Дата обращения: 9 апреля 2023. Архивировано 9 апреля 2023 года.
- ↑ 1 2 Floating-point tricks | IEEE Journals & Magazine | IEEE Xplore. Дата обращения: 17 августа 2022. Архивировано 17 августа 2022 года.. Копия на Yumpu Архивная копия от 9 апреля 2023 на Wayback Machine
- ↑ 1 2 Fast reciprocal square root… in 1997?! — Shane Peelar’s Blog. Дата обращения: 17 августа 2022. Архивировано 11 октября 2022 года.
- ↑ Beyond3D — Origin of Quake3’s Fast InvSqrt(). Дата обращения: 4 октября 2019. Архивировано 10 апреля 2017 года.
- ↑ PFRSQRT — Вычислить приблизительное значение обратной величины квадратного корня от короткого вещественного значения — Club155.ru. Дата обращения: 4 октября 2019. Архивировано 16 октября 2019 года.
- ↑ RSQRTSS — Compute Reciprocal of Square Root of Scalar Single-Precision Floating-Point Value. Дата обращения: 6 октября 2019. Архивировано 12 августа 2019 года.
- ↑ Some Assembly Required » Blog Archive » Timing square root
- ↑ z88dk/libsrc/_DEVELOPMENT/math/float/math32 at master · z88dk/z88dk · GitHub. Дата обращения: 9 апреля 2023. Архивировано 9 апреля 2023 года.
- ↑ https://web.archive.org/web/20150511044204/http://www.daxia.com/bibis/upload/406Fast_Inverse_Square_Root.pdf
- ↑ 1 2 3 4 Швидке обчислення оберненого квадратного кореня з використанням магічної константи — аналітичний підхід. Дата обращения: 12 июня 2022. Архивировано 17 апреля 2022 года.
- ↑ 1 2 3 Это норма: что такое карты нормалей и как они работают / Хабр. Дата обращения: 4 июля 2022. Архивировано 10 июля 2020 года.
- ↑ 1 2 Řrřlog :: Improving the fast inverse square root. Дата обращения: 8 апреля 2023. Архивировано 8 апреля 2023 года.
Ссылки[править | править код]
- C. Lomont, Fast inverse square root, Technical Report, 2003.
- A Brief History of InvSqrt by Matthew Robertson
- 0x5f3759df, further investigations into accuracy and generalizability of the algorithm by Christian Plesner Hansen



























![{\displaystyle -{\tfrac {1}{2}}[I_{x}-L(B-\sigma )]\approx I_{y}-L(B-\sigma )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8abf0f8f968728e25f7478e8f895695cf4285173)
![{\displaystyle y\approx I^{-1}\left[{\tfrac {3}{2}}L(B-\sigma )-{\tfrac {1}{2}}I_{x}\right]\equiv I^{-1}\left(Q-{\tfrac {1}{2}}I_{x}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a008aeb1e41d6da4efce03b1aba2380064eb92dd)




















