Гиперзвуковая скорость

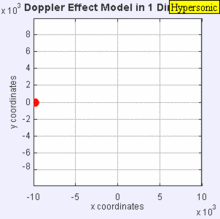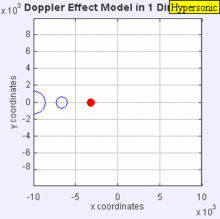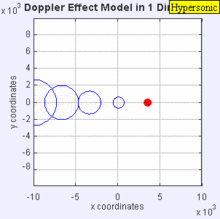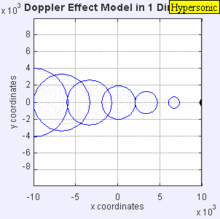
Ги́перзвуковая ско́рость (ГС) в аэродинамике — скорости, которые значительно превосходят скорость звука в атмосфере.
Начиная с 1970-х годов, понятие обычно относят к сверхзвуковым скоростям с числами Маха (М) выше 5.
Общие сведения[править | править код]
Полет на гиперзвуковой скорости является разновидностью сверхзвукового режима полета и осуществляется в сверхзвуковом потоке газа. Сверхзвуковой поток воздуха коренным образом отличается от дозвукового, и динамика полета самолета при скоростях выше скорости звука (выше 1,2 М) кардинально отличается от дозвукового полета (до 0,75 М, диапазон скоростей от 0,75 до 1,2 М называется трансзвуковой скоростью).
Определение нижней границы гиперзвуковой скорости обычно связано с началом процессов ионизации и диссоциации молекул в пограничном слое (ПС) около аппарата, который движется в атмосфере, что начинает происходить примерно при М>5 примерно 6000км/ч. Также данная скорость характеризуется тем, что сверхзвуковой прямоточный воздушно-реактивный двигатель с дозвуковым сгоранием топлива (СПВРД) становится менее эффективным по сравнению с гиперзвуковым ПВРД (ГПВРД), в котором сгорание топлива осуществляется при сверхзвуковых скоростях потока. СПВРД по сравнению с ГПВРД при той же скорости полета требует более сильного торможения потока воздуха перед его попаданием в камеру сгорания. Это обуславливает бо́льшие потери давления на участке торможения потока в СПВРД. В то же время в ГПВРД сгорание топлива при сверхзвуковой скорости потока сопровождается бо́льшими потерями давления по сравнению с потерями при сгорании топлива в дозвуковом потоке в СПВРД. При прочих равных условиях, чем ниже суммарные потери давления в проточном тракте ПВРД, тем выше его эффективность. Условия полета, при которых суммарные потери в проточных трактах СПВРД и ГПВРД оказываются одинаковыми, принимаются за границу между сверхзвуковыми и гиперзвуковыми скоростями. Положение данной границы весьма условно и зависит от многих факторов. Так, например, для двигателей, использующих в качестве топлива водород, ввиду бо́льшей удельной теплоты его сгорания нижняя граница гиперзвуковых скоростей будет соответствовать более высоким числам Маха полета, нежели чем для аналогичных двигателей, работающих на керосине.
Характеристики потока[править | править код]
В то время как определение гиперзвукового потока (ГП) достаточно спорно по причине отсутствия четкой границы между сверхзвуковым и гиперзвуковым потоками, ГП может характеризоваться определенными физическими явлениями, которые уже не могут быть проигнорированы при рассмотрении, а именно:
- тонкий слой ударной волны;
- образование вязких ударных слоев;
- появление волн неустойчивости в ПС, не свойственных до- и сверхзвуковым потокам[1];
- высокотемпературный поток[2].
Тонкий слой ударной волны[править | править код]
По мере увеличения скорости и соответствующих чисел Маха, плотность позади ударной волны также увеличивается, что соответствует уменьшению объема сзади от ударной волны благодаря сохранению массы. Поэтому, слой ударной волны, то есть объем между аппаратом и ударной волной становится тонким при высоких числах Маха, создавая тонкий пограничный слой вокруг аппарата.
Образование вязких ударных слоев[править | править код]
Часть большой кинетической энергии, заключенной в воздушном потоке, при М > 3 (вязкое течение) преобразуется во внутреннюю энергию за счет вязкого взаимодействия. Увеличение внутренней энергии реализуется в росте температуры. Так как градиент давления, направленный по нормали к потоку в пределах пограничного слоя, приблизительно равен нулю, существенное увеличение температуры при больших числах Маха приводит к уменьшению плотности. Таким образом, ПС на поверхности аппарата растет и при больших числах Маха сливается с тонким слоем ударной волны вблизи носовой части, образуя вязкий ударный слой.
Появление волн неустойчивости в ПС, не свойственных до- и сверхзвуковым потокам[править | править код]
В важной проблеме перехода ламинарного течения в турбулентное для случая обтекания летательного аппарата ключевую роль играют волны неустойчивости, образующиеся в ПС. Рост и последующее нелинейное взаимодействие таких волн преобразует изначально ламинарный поток в турбулентное течение. На до- и сверхзвуковых скоростях ключевую роль в ламинарно-турбулентном переходе играют волны Толмина-Шлихтинга, имеющие вихревую природу. Начиная с М = 4,5 в ПС появляются и начинают доминировать волны акустического типа (II мода или мэкавская мода), благодаря которым происходит переход в турбулентность при классическом сценарии перехода (существует также by-pass механизм перехода)[1].
Высокотемпературный поток[править | править код]
Высокоскоростной поток в лобовой точке аппарата (точке или области торможения) вызывает нагревание газа до очень высоких температур (до нескольких тысяч градусов). Высокие температуры, в свою очередь, создают неравновесные химические свойства потока, которые заключаются в диссоциации и рекомбинации молекул газа, ионизации атомов, химическим реакциям в потоке и с поверхностью аппарата. В этих условиях могут быть существенны процессы конвекции и радиационного теплообмена[2].
Параметры подобия[править | править код]
Параметры газовых потоков принято описывать набором критериев подобия, которые позволяют свести практически бесконечное число физических состояний в группы подобия и которые позволяют сравнивать газовые потоки с разными физическими параметрами (давление, температура, скорость и пр.) между собой. Именно на этом принципе основано проведение экспериментов в аэродинамических трубах и перенос результатов этих экспериментов на реальные летательные аппараты, несмотря на то, что в трубных экспериментах размер моделей, скорости потока, тепловые нагрузки и пр. могут сильно отличаться от режимов реального полёта, в то же время, параметры подобия (числа Маха, Рейнольдса, Стантона и пр.) соответствуют полётным.
Для транс- и сверхзвукового или сжимаемого потока, в большинстве случаев таких параметров как число Маха (отношение скорости потока к местной скорости звука) и Рейнольдса достаточно для полного описания потоков. Для гиперзвукового потока данных параметров часто бывает недостаточно. Во-первых, описывающие форму ударной волны уравнения становятся практически независимыми на скоростях от 10 М. Во-вторых, увеличенная температура гиперзвукового потока означает, что эффекты, относящиеся к неидеальным газам становятся заметными.
Учет эффектов в реальном газе означает бо́льшее количество переменных, которые требуются для полного описания состояния газа. Если стационарный газ полностью описывается тремя величинами: давлением, температурой, теплоёмкостью (адиабатическим индексом), а движущийся газ описывается четырьмя переменными, которая включает еще скорость, то горячий газ в химическом равновесии также требует уравнений состояния для составляющих его химических компонентов, а газ с процессами диссоциации и ионизации должен еще включать в себя время как одну из переменных своего состояния. В целом это означает, что в любое выбранное время для неравновесного потока требуется от 10 до 100 переменных для описания состояния газа. Вдобавок, разреженный гиперзвуковой поток (ГП), обычно описываемый в терминах чисел Кнудсена, не подчиняются уравнениям Навье-Стокса и требуют их модификации. ГП обычно категоризируется (или классифицируется) с использованием общей энергии, выраженной с использованием общей энтальпии (мДж/кг), полного давления (кПа) и температуры торможения потока (К) или скорости (км/с).
Для инженерных приложений У. Д. Хэйес развил параметр подобия, близкий к правилу площадей Виткомба, который позволяет инженерам применять результаты одной серии испытаний или расчетов, выполненных для одной модели, к разработке целого семейства подобных конфигураций моделей, при этом не проводя дополнительных испытаний или подробных расчетов.
Список режимов[править | править код]
Гиперзвуковой поток подразделяется на множество частных случаев. Отнесение ГП к одному или другому режиму потока представляется сложной задачей по причине «размытия» границ состояний, при которых это явление в газе обнаруживается или становится заметным с точки зрения используемого математического моделирования.
Идеальный газ[править | править код]
В данном случае, проходящий воздушный поток может рассматриваться как поток идеального газа. ГП в данном режиме все еще зависит от чисел Маха и моделирование руководствуется температурными инвариантами, а не адиабатической стенкой, что имеет место при ме́ньших скоростях. Нижняя граница этой области соответствует скоростям около 5 М, где СПВРД с дозвуковым сгоранием становятся неэффективными, и верхняя граница соответствует скоростям в районе 10—12 М.
Идеальный газ с двумя температурами[править | править код]
Является частью случая режима потока идеального газа с большими значениями скорости, в котором проходящий воздушный поток может рассматриваться химически идеальным, но вибрационная температура и вращательная температура газа[3] должны рассматриваться отдельно, что приводит к двум отдельным температурным моделям. Это имеет особое значение при проектировании сверхзвуковых сопел, где вибрационное охлаждение из-за возбуждения молекул становится важным.
Диссоциированный газ[править | править код]
В данном случае молекулы газа начинают диссоциировать по мере того, как они вступают в контакт с генерируемой движущимся телом ударной волной. Поток начинает различаться для каждого конкретного рассматриваемого газа со своими химическими свойствами. Способность материала корпуса аппарата служить катализатором в этих реакциях играет роль в расчете нагрева поверхности, что означает появление зависимости гиперзвукового потока от химических свойств движущегося тела. Нижняя граница режима определяется первым компонентом газа, который начинает диссоциировать при данной температуре торможения потока, что соответствует азоту при 2000 К. Верхняя граница этого режима определяется началом процессов ионизации атомов газа в ГП.
Ионизированный газ[править | править код]
В данном случае, количество потерянных атомами электронов становится существенным и электроны должны моделироваться отдельно. Часто температура электронного газа рассматривается изолировано от других газовых компонентов. Этот режим соответствует диапазону скоростей ГП 10—12 км/с (> 25 М) и состояние газа в данном случае описывается с помощью моделей безизлучательной или неизлучающей плазмы.
Режим доминирования лучевого переноса[править | править код]
На скоростях выше 12 км/с передача тепла аппарату начинает происходить в основном через лучевой перенос, который начинает доминировать над термодинамическим переносом вместе с ростом скорости. Моделирование газа в данном случае подразделяется на два случая:
- оптически тонкий — в данном случае предполагается, что газ не перепоглощает излучение, которое приходит от других его частей или выбранных единиц объема;
- оптически толстый — где учитывается поглощение излучения плазмой, которое потом переизлучается в том числе и на тело аппарата.
Моделирование оптически толстых газов является сложной задачей, так как из-за вычисления радиационного переноса в каждой точке потока объем вычислений растет экспоненциально вместе с ростом количества рассматриваемых точек.
См. также[править | править код]
Примечания[править | править код]
Ссылки[править | править код]
- Anderson, John. Hypersonic and High-Temperature Gas Dynamics Second Edition (англ.). — AIAA Education Series, 2006. — ISBN 1563477807.
- NASA’s Guide to Hypersonics (англ.).
- Hypersonics Group at Imperial College (англ.).
- University of Queensland Centre for Hypersonics (англ.).