Четвёртая проблема Гильберта

Четвёртая проблема Гильберта в списке проблем Гильберта касается базовой системы аксиом геометрии. Проблема состоит в том, чтобы

«Определить все с точностью до изоморфизма реализации систем аксиом классических геометрий (Евклида, Лобачевского и эллиптической), если в них опустить аксиомы конгруэнтности, содержащие понятия угла, и пополнить эти системы аксиомой неравенства треугольника».

В случае плоскости, если принять аксиому непрерывности приходим к задаче, поставленной Дарбу:

«Найти на плоскости все вариационные задачи, решениями которых являются все прямые линии на плоскости».

Плоские метрики

Прямые, соединяющие соответствующие вершины треугольников, проходят через одну точку — она расположена слева. Соответственно три точки, в которых пересекаются продолжения трех пар соответствующих сторон треугольников, лежат на одной прямой — она фиолетового цвета.

Верна теорема Дезарга:
Если два треугольника расположены на плоскости таким образом, что прямые, соединяющие соответственные вершины треугольников, проходят через одну точку, то три точки, в которых пересекаются продолжения трёх пар соответственных сторон треугольников, лежат на одной прямой

Необходимым условием для решения IV проблемы Гильберта является требование, чтобы метрическое пространство, удовлетворяющее аксиомам этой проблемы, являлось дезарговым, то есть должны выполняться условия:

• Если пространство двумерное, необходимо, чтобы выполнялось теорема Дезарга и обратная к ней;
• Если размерность пространства больше двух, то необходимо, чтобы любые три точки лежали на одной плоскости.

Для дезарговых пространств Гамель доказал, что всякое решение проблемы Гильберта можно представить в вещественном проективном пространстве $\mathbb {R} \mathrm {P} ^{n}$ или в выпуклой области $\mathbb {R} \mathrm {P} ^{n},$ если определить конгруэнтность отрезков через равенство их длин в специальной метрике, для которой прямые проективного пространства являются геодезическими.

Такие метрики называются плоскими или проективными.

Таким образом, решение проблемы Гильберта было сведено к задаче конструктивного определения всех полных плоских метрик.

Гамель решил эту задачу в предложении достаточной регулярности метрики. Однако, как показывают простые примеры, регулярные плоские метрики далеко не исчерпывают все плоские метрики. Из аксиом рассматриваемых геометрией следует только непрерывность метрик. Поэтому полное решение проблемы Гильберта предполагает конструктивное определение всех непрерывных плоских метрик.

Предыстория IV проблемы Гильберта

Модель Кэли-Клейна геометрии Лобачевского

До 1900 была известна интерпретация Кэли-Клейна геометрии Лобачевского в единичном круге, где прямыми являются хорды круга, а расстояние между точками определялся как логарифм сложного отношения четырех точек.

Для двумерных римановых метрик Э. Бельтрами (1835—1900) доказал, что единственными плоскими метриками являются метрики постоянной кривизны.

Для многомерных римановых метрик это утверждение было доказано Э. Картаном в 1930 году.

В 1890 году Г. Минковский в связи с теорией чисел ввел то, что мы сейчас называем конечномерные банаховы пространства.

Пространство Минковского

Пространство Минковского

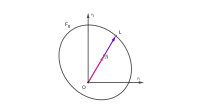
$F_{0}\subset \mathbb {E} ^{n}$ — компактная замкнутая выпуклая гиперповерхность в евклидовом пространстве, заданная неявно

$F_{0}=\{y\in E^{n}:F(y)=1\}.$

Функция $F=F(y)$ удовлетворяет условиям:

1. $F(y)\geqslant 0,\qquad F(y)=0\Leftrightarrow y=0$;
2. $F(\lambda y)=\lambda F(y),\qquad \lambda \geqslant 0$;
3. $F(y)\in C^{k}(E^{n}\setminus \{0\}),\qquad k\geqslant 3$;
4. ${\frac {\partial ^{2}F^{2}}{\partial y^{i}\partial y^{j}}}\xi ^{i}\xi ^{j}>0$.

Зададим длину вектора OA так:

$||OA||_{M}={\frac {||OA||_{\mathbb {E} }}{||OL||_{\mathbb {E} }}}.$

Пространство с такой метрикой называется пространством Минковского.

Гиперповерхность $F_{0}$ может быть нерегулярной выпуклой поверхностью. Метрика, задаваемая таким образом, является плоской.

Финслеровы пространства

Пусть M — гладкое, конечномерное многообразие, $(x,y)\in TM$ — касательное расслоение. Функция $F(x,y)\colon TM\rightarrow [0,+\infty )$ называется финслеровой метрикой, если

1. $F(x,y)\in C^{k}(TM\setminus \{0\}),\qquad k\geqslant 3$;
2. Для каждой точки $x\in M$, ограничение функции $F(x,y)$ на $T_{x}M$ является нормой Минковского.

$(M,F)$ называется финслеровым пространством.

Геометрия Гильберта

Метрика Гильберта

$U\subset (\mathbb {E} ^{n+1},\|.\|_{\mathbb {E} })$ — ограниченное открытое выпуклое множество с границей класса C² и положительными нормальными кривизнами. По аналогии с пространством Лобачевского, гиперповерхность $\partial U$ называется абсолютом геометрии Гильберта.

Метрика Гильберта

$d_{U}(p,q)={\frac {1}{2}}\ln {\frac {\|q-q_{1}\|_{E}}{\|q-p_{1}\|_{E}}}\times {\frac {\|p-p_{1}\|_{E}}{\|p-q_{1}\|_{E}}}.$

Финслерова метрика Гильберта

$d_{U}$ индуцирует финслерову метрику Гильберта $F_{U}$ на U для любых $x\in U$ и $y\in T_{x}U$ (см. рис.)

$F_{U}(x,y)={\frac {1}{2}}\|y\|_{\mathbb {E} }\left({\frac {1}{\|x-x_{+}\|_{\mathbb {E} }}}+{\frac {1}{\|x-x_{-}\|_{\mathbb {E} }}}\right).$

Эта метрика так же является плоской.

Д. Гильберт ввел ее в 1895 году как обобщение геометрии Лобачевского. Когда гиперповерхность $\partial U$ является эллипсоидом, то получаем геометрию Лобачевского.

Метрика Функа

В 1930 году Функ ввел несимметричную метрику. Она задана в области, ограниченной замкнутой выпуклой гиперповерхностью и также является плоской.

σ-метрики

Достаточное условие плоских метрик

Первый вклад в решение IV проблемы Гильберта сделал Гамель. Он доказал следующее утверждение.

Теорема. Если регулярная финслерова метрика $F(x,y)=F(x_{1},....x_{n},y_{1},...,y_{n})$ удовлетворяет условию

${\frac {\partial ^{2}F^{2}}{\partial x^{i}\partial y^{j}}}={\frac {\partial ^{2}F^{2}}{\partial x^{j}\partial y^{i}}},\,i,j=1..n,$

то она плоская.

Формула Крофтона

Рассмотрим множество ориентированных прямых на плоскости. Прямая задается параметрами $\rho ,\varphi ,$ где $\rho$ — расстояние до прямой от начала координат, $\varphi$ — угол, который образует прямая с осью Ox. Тогда множество ориентированных прямых гомеоморфно круговому цилиндру единичного радиуса, где элемент площади $dS=d\rho d\varphi$. Пусть $\gamma$ — спрямляемая кривая на плоскости. Тогда ее длина

$L={\frac {1}{4}}\iint \limits _{\Omega }n(\rho ,\varphi )dpd\varphi$,

где $\Omega$ — множество прямых, которые пересекают данную кривую, $n(p,\varphi )$ — число пересечений прямой с кривой. Это показал М. Крофтон в 1870 году.

Аналогичное утверждение имеет место в проективном пространстве.

Мера Бляшке-Буземана

В 1966 году Г. Буземан, выступая на Международном математическом конгрессе в Москве, ввел новый класс плоских метрик. Г. Буземан ввел на множестве прямых проективной плоскости $\mathbb {R} \mathrm {P} ^{2}$ вполне аддитивную неотрицательную меру $\sigma$, которая удовлетворяет следующим условиям:

1. $\sigma (\tau P)=0$, где $\tau P$ — множество прямых, проходящих через точку P;
2. $\sigma (\tau X)>0$, где $\tau X$ — множество прямых, проходящих через некоторое множество X, содержащее отрезок прямой;
3. $\sigma (\mathbb {R} \mathrm {P} ^{n})$ конечна.

Если мы рассмотрим $\sigma$-метрику, задаваемую в произвольной выпуклой области $\Omega$ проективного пространства $\mathbb {R} \mathrm {P} ^{2}$, то условие 3) заменяется требованием, чтобы для любого множества H, — такого, что H содержится в $\Omega$, замыкание H не пересекается с границей $\Omega$, выполняется

$\sigma (\pi H)<\infty$.

С помощью такой меры определяется $\sigma$-метрика в $\mathbb {R} \mathrm {P} ^{2}$:

$|x,y|=\sigma \left(\tau [x,y]\right),$

где $\tau [x,y]$ — множество прямых, пересекающих отрезок $[x,y]$.

Неравенство треугольника для этой метрики следует из теоремы Паша.

Теорема. $\sigma$-метрика в $\mathbb {R} \mathrm {P} ^{2}$ является плоской метрикой, то есть геодезические в этой метрике являются прямыми проективного пространства.

Но Буземан был далек от мысли, что $\sigma$-метрики исчерпывают все плоские метрики. Он писал: «… Свобода в выборе метрик при задании геодезических в случае неримановых метрик так велика, что можно сомневаться, существует ли в действительности убедительная характеристика всех дезарговых пространств…».

Двумерный случай

Теорема Погорелова

Удивительной оказалась теорема, доказанная в 1973 году А. В. Погореловым.

Теорема. Любая двумерная непрерывная полная плоская метрика является $\sigma$-метрикой.

Тем самым IV проблема Гильберта для двумерного случая полностью решена.

Другие доказательства

В 1976 году Р. Б. Амбарцумян дал другое доказательство IV проблемы Гильберта. Его доказательство связано с тем, что в двумерном случае вся мера восстанавливается по ее значениям на двухугольниках. И тогда она задается на треугольниках аналогично тому, как задается площадь треугольника на сфере. На невырожденных треугольниках она положительна так как выполняется неравенство треугольника, и дальше мера определяется на всех борелевских множествах. Но эта конструкция не обобщается по размерности. Это связано с III проблемой Гильберта, которую решил М. Ден. В двумерном случае равновеликие многоугольники равносоставлены. В большей размерности, как показал М. Ден, это неверно.

Трехмерный случай

Для случая n=3 А. В. Погорелов доказал следующую теорему

Теорема. Любая трехмерная регулярная непрерывная полная плоская метрика является $\sigma$-метрикой.

Однако в трехмерном случае $\sigma$-меры могут принимать как положительные, так и отрицательные значения. Необходимыми и достаточными условиями того, чтобы регулярная метрика, задаваемая функцией множества $\sigma$, была плоской, являются следующие три условия:

1. значение $\sigma$ на любой плоскости равняется нулю;
2. значение $\sigma$ в любом конусе неотрицательно;
3. значение $\sigma$ положительно, если конус содержит внутренние точки.

Кроме того, А. В. Погорелов показал, что всякая полная непрерывная плоская метрика в трехмерном случае является пределом регулярных $\sigma$-метрик с равномерной сходимостью в любой компактной подобласти области задания этой метрики. Такие метрики он назвал обобщенными $\sigma$-метриками.

Таким образом, А. В. Погорелову удалось доказать, что

Теорема. Всякая полная непрерывная плоская метрика в трехмерном случае является $\sigma$-метрикой в обобщенном смысле.

Г. Буземан в рецензии на перевод книги А. В. Погорелова ``Четвертая проблема Гильберта писал: "«В соответствие с духом времени Гильберт ограничивался размерностями n = 2, 3. А. В. Погорелов также ограничился этими размерностями. Хотя реальная разница между n = 2 и n>2. Метод Погорелова работает и при n>3 только требует больше технических подробностей.»

Многомерный случай

Многомерный случай IV проблемы Гильберта был изучен З. И. Сабо. В 1986 году он доказал, как он сам пишет, обобщенную теорему Погорелова: Теорема. Любое n-мерное Дезаргово пространство класса $C^{n+2},n>2$ порождается конструкцией Бляшке-Буземана.

$\sigma$-мера, которая порождает плоскую меру, обладает следующими свойствами:

1. $\sigma$-мера гиперплоскостей, которые проходят через фиксированную точку, равна нулю.
2. $\sigma$-мера множества гиперплоскостей, которые пересекают два отрезка [x, y], [y, z], где x, y, z не коллинеарны, положительна.

В этой же статье приведен пример плоской метрики, которая не порождается конструкцией Бляшке-Буземана. З. И. Сабо описал все непрерывные плоские метрики на языке обобщенных функций.

IV проблема Гильберта и выпуклые тела

IV проблема Гильберта также тесно связана со свойствами выпуклых тел. Выпуклый многогранник называется зонотопом, если он является суммой (по Минковскому) отрезков. Выпуклое тело, которое является пределом зонотопов в метрике Бляшке — Хаусдорфа, называется зоноидом. Для зоноидов опорная функция представляется в виде

$h(x)=\int \limits _{S^{n-1}}|\langle x,u\rangle |\partial \sigma (u),$

где $\sigma (u)$ — четная положительная мера Бореля на сфере $S^{n-1}$.

Пространство Минковского тогда и только тогда порождается конструкцией Бляшке-Буземана, когда опорная функция индикатрисы имеет вид приведенный выше, где $\sigma (u)$ — четная не обязательно знакопостоянная мера Бореля. Тела, ограниченными такими гиперповерхностями называются обобщенными зоноидами.

Октаэдр $|x_{1}|+|x_{2}|+|x_{3}|\leqslant 1$ в евклидовом пространстве $E^{3}$ не является обобщенным зоноидом. Тогда из утверждения выше следует, что плоская метрика пространства Минковского с нормой $\|x\|=\max\{|x_{1}|,|x_{2}|,|x_{3}|\}$, не порождается конструкцией Бляшке-Буземана.

Обобщения IV проблемы Гильберта

Найдено соответствие между плоскими n-мерными финслеровыми метриками и специальными симплектическими формами на грассмановом многообразии $G(n+1,2)$ в $E^{n+1}$.

Рассматривались периодические решения IV проблемы Гильберта:

1. Пусть (M, g) есть компактное локально евклидово риманово многообразие. На нем задана $C^{2}$ финслерова метрика, геодезические которой совпадают с метрикой g. Тогда финслерова метрика есть сумма локально Минковской метрики и замкнутой 1-формы.

1. Пусть (M, g) есть компактное симметрическое риманово пространство ранга больше один. Если F симметрическая $C^{2}$ финслерова метрика, геодезические которой совпадают с геодезическими римановой метрики g, то (M, F) — симметрическое финслерово пространство.

Другое изложение IV проблемы Гильберта есть в работе Пайви 2003 года.

Нерешенные задачи

1. Не решена IV проблема Гильберта для несимметричного расстояния.
2. Неизвестен аналог последней теоремы для случая симметрических пространств ранга один.
3. Описать метрики на $\mathbb {R} \mathrm {P} ^{n}$, для которых k-плоскости минимизируют k-площадь (Г. Буземан).