Марковский процесс принятия решений
Марковский процесс принятия решений (МППР, англ. Markov decision process, MDP) — математический формализм для марковского дискретного стохастического процесса управления, основа для моделирования последовательного принятия решений в ситуациях, где результаты частично случайны и частично зависят от лица, принимающего решения. МППР используется во множестве областей, включая робототехнику, автоматизированное управление, экономику и производство. Подход обучения с подкреплениями, основанный на данной модели, применяется, например, в нейронной сети AlphaZero.
Определение[править | править код]

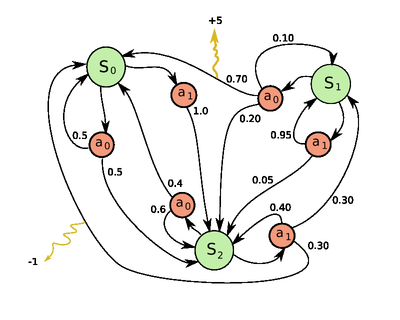
Марковские процессы принятия решений представляют собой инструмент для постановки задачи обучения, где достижение цели осуществляется через взаимодействие и последовательное принятие решений. Окружающая среда (или просто среда), представляет собой сторону, с которой взаимодействует агент. Агент выбирает действия, в то время как среда реагирует на эти действия и предоставляет новые ситуации для агента. Кроме того, среда генерирует вознаграждения — числовые значения, которые агент стремится максимизировать с течением времени путем выбора действий. Инженерам будут более понятны термины: агент — устройство управления или контроллер, среда — управляемая система, действие — управляющий сигнал.[1]
Формально определить марковский процесс принятия решений можно, задав 4-кортеж , где[1]
- — конечное множество состояний среды, из которых агент наблюдает в момент времени ,
- — конечное множество действий, доступных из состояния , из которых агент может выбрать для момента времени действие ,
- — вероятность перехода состояний. То есть, вероятность того, что действие в состоянии в момент времени приведёт в состояние в момент ,
- вознаграждение, получаемое после перехода в состояние из состояния при совершении действия .
Совместно агент и среда порождают траекторию .
Стратегия — функция (в общем случае распределение вероятностей), сопоставляющая состоянию действие. При наличии такой функции МППР можно рассматривать как Марковскую цепь.
Формализм марковских процессов принятия решений является важной абстракцией задачи обучения целеустремленного агента в процессе взаимодействия. Он позволяет утверждает, что независимо от деталей механизмов восприятия, памяти и управления, а также от цели, которую преследует агент, любая задача обучения целенаправленному поведению может быть сведена к трем сигналам, которыми агент обменивается с окружающей средой: сигнал, представляющий выбор агента (действие), сигнал причины такого выбора (состояние среды), и сигнал, определяющий цель агента (вознаграждение). Этот формализм не всегда достаточен для описания всех задач обучения принятию решений, но он широко применяется и полезен.[1]
Цель оптимизации[править | править код]
Решить марковский процесс принятия решений означает найти оптимальную стратегию, максимизирующую вознаграждение (функцию ценности). Самая простая функция ценности — это математическое ожидание формального ряда , где , а математическое ожидание берётся в соответствии с распределением вероятности , но такую функцию можно использовать только если ряд сходится всегда, что обычно означает наличие конечного состояния МППР — такого, что и . Если же сходимость ряда не гарантируется, можно:
- Рассмотреть только конечное число слагаемых
- Ввести — коэффициент обесценивания (дисконтирования) , который контролирует предпочтение агентом мгновенных вознаграждений по сравнению с вознаграждениями в будущем
На практике второй вариант более гибкий, так как учитывает более долгосрочную перспективу и чаще используется именно он.
Для максимизации такого ряда вводят две функции:
- Функция полезности состояния , где математическое ожидание берётся в соответствии с распределением
- Функция полезности действия , где математическое ожидание берётся в соответствии с
А также их максимумы по всем стратегиям:
Можно доказать, что эти функции также являются функциями полезности состояния и полезности действия соответственно, а также, что они достигаются на детерминированной стратегии. Заметим, что по функции можно восстановить её стратегию, которая будет оптимальной.
Сравнение стратегий[править | править код]
Чтобы дать формальное определение оптимальной стратегии необходимо ввести отношение порядка на множестве стратегий. . Наибольшая стратегия называется оптимальной.
Можно доказать, что оптимальная стратегия существует.
Алгоритмические реализации[править | править код]
Большинство алгоритмов марковских процессов принятия решений основаны на итерации уравнения Беллмана с фиксированной точкой. Примеры включают итерацию состояния среды (англ. value iteration), итерацию стратегии (англ. policy iteration), метод временных разностей (англ. time difference, TD), Q-обучение и т. д. Анализ этих алгоритмов в табличном случае и случае линейной аппроксимации функции часто использует свойство сжатия оператора Беллмана. В последнее десятилетие нелинейные аппроксимации, такие как нейронные сети, стали более популярными. Однако для нелинейных аппроксимаций функций это свойство сжатия уже не выполняется, что часто приводит к нестабильности. Было предложено множество вариантов и модификаций для стабилизации обучения, например, DQN (англ. Deep Q-Network — «глубокая Q-сеть»), A3C (англ. Asynchronous Advantage Actor-Critic — «агент-критик с асинхронным преимуществом»). Однако для этих алгоритмов по-прежнему отсутствуют теоретические гарантии.[2]
Расширения[править | править код]
Дискретные марковские процессы принятия решений хорошо изучены. Существуют расширения для непрерывных состояний среды с линейной или нелинейной аппроксимацией функций, случаев частичной наблюдаемости (англ. partially observable MDP), структурированных МППР (например, динамические байесовские сети англ. DBN) и другие, но алгоритмы становятся намного менее устойчивыми.[3]
См. также[править | править код]
Примечания[править | править код]
- ↑ 1 2 3 4 Саттон, Барто, 2020.
- ↑ Lexing Ying and Yuhua Zhu (2022), "A Note on Optimization Formulations of Markov Decision Processes", Commun. Math. Sci., 20 (3), International Press: 727—745
{{citation}}: Игнорируется текст: "publication" (справка) - ↑
Marcus Hutter (2009), "Feature Reinforcement Learning: Part I. Unstructured MDPs", Journal of Artificial General Intelligence, 1: 3–24, doi:10.2478/v10229-011-0002-8
{{citation}}: Игнорируется текст: "publication" (справка)
Литература[править | править код]
- Саттон Р. С., Барто Э. Дж. Обучение с подкреплением: Введение = Reinforcement Learning. — 2-е изд.. — Москва: ДМК Пресс, 2020. — С. 552.















![{\displaystyle E\left[\sum _{t=0}^{\infty }{R_{a_{t}}(s_{t},s_{t+1})}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca2c9ba2c11c4a2e83cb7792ecbfdf18a4fd667c)




![{\displaystyle E\left[\sum _{t=0}^{N}{R_{a_{t}}(s_{t},s_{t+1})}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/963821767da58f538ca3d8b8fbb83621f9bfb88b)
![{\displaystyle \gamma \in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbc65bc4fa0e25a8305259b234865def64ac1a8a)
![{\displaystyle E\left[\sum _{t=0}^{\infty }{\gamma ^{t}R_{a_{t}}(s_{t},s_{t+1})}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/712f6adf8034f0df53957e45ab0f35441bef017e)
![{\displaystyle V_{\pi }(s)=E\left[\sum _{t=0}^{\infty }{\gamma ^{t}R_{a_{t}}(s_{t},s_{t+1})}\mid s_{0}=s,a_{t}={\pi }(s_{t})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8bdeb8cc25b4f77f65aae800b2822a14cdb80e57)
![{\displaystyle Q_{\pi }(s,a)=E\left[\sum _{t=0}^{\infty }{\gamma ^{t}R_{a_{t}}(s_{t},s_{t+1})}\mid s_{0}=s,a_{0}=a,a_{t}={\pi }(s_{t})\;\forall t\geqslant 1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02451ee3c5f233b8883674a498de99a6a7bb070f)



