Теория гравитации Лесажа
Необходимо проверить качество перевода, исправить содержательные и стилистические ошибки. |
В 1690 году женевский математик[1] Никола Фатио де Дюилье и в 1756 году другой женевский математик, Жорж Луи ЛеСаж, предложили простую кинетическую теорию гравитации, которая дала механическое объяснение закону всемирного тяготения Ньютона[2]. Из-за того, что работа Фатио не была широко известна и оставалась неопубликованной долгое время, именно описание теории Ле Сажем стало темой повышенного интереса в конце XIX века, когда последняя была изучена в контексте только что открытой кинетической теории газов[3]. Это механическое объяснение гравитации не получило широкого признания, и к началу XX века теория в целом считалась опровергнутой, в основном из-за проблем, поднятых Максвеллом[4], Пуанкаре[5]. Кроме того, во втором десятилетии XX века Альберт Эйнштейн создал общую теорию относительности, правда признание к ней пришло несколько позже. Хотя теория Ле Сажа всё ещё изучается некоторыми исследователями, она обычно не рассматривается основным научным сообществом как жизнеспособная теория.
Основная теория[править | править код]

Нет чистой направленной силы
Теория утверждает, что сила гравитации — это результат движения крошечных частиц, двигающихся на высокой скорости во всех направлениях во Вселенной. Интенсивность потока частиц предполагается одинаковой во всех направлениях. Таким образом, изолированный объект A ударяется частицами со всех сторон, в результате чего он подвергается давлению внутрь объекта, но не подвергается направленной силе P1.
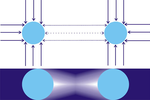
Однако в случае присутствия второго объекта B часть частиц, которые иначе бы ударили по объекту A со стороны B, перехватывается. Объект B работает как экран, т.е. с направления В объект A ударит меньше частиц, чем с противоположного направления. Аналогично и объект B будет ударен меньшим количеством частиц со стороны A по сравнению с противоположной стороной. То есть можно сказать, что объекты A и B «экранируют» друг друга, и оба тела прижимаются друг к другу результирующим дисбалансом сил (P2). Таким образом, кажущееся притяжение между телами в данной теории на самом деле является уменьшенным давлением на тело со стороны других тел. По этой причине данную теорию иногда называют «теневой гравитацией», хотя наиболее часто встречается название «гравитация Лесажа».
Природа столкновений[править | править код]

Если соударение тела A и гравитационной частицы полностью упруго, интенсивность отражённых частиц будет настолько же сильной, как и приходящих частиц, т.е. чистая направленная сила не возникнет. Данное утверждение верно и в том случае, если мы введём второе тело В, которое будет действовать как экран для гравитационных частиц в направлении тела A. Гравитационная частица C, которая в обычной ситуации ударила бы по объекту A, блокируется В, но другая частица D, которая в обычной ситуации не ударила бы по A, перенаправляется упругим отражением от объекта B на объект A и, следовательно, заменяет C. Таким образом, если столкновение полностью упруго, отражённые частицы между объектами A и B полностью компенсируют любой «экранирующий» эффект. Чтобы объяснить суть гравитационной силы, мы должны предположить, что соударение частиц не является полностью упругим или хотя бы то, что отражённые частицы замедляются, т.е. их импульс уменьшается после столкновения. Это приведёт к тому, что от объекта А отходит поток с уменьшенным импульсом, но приходит поток с неизменённым импульсом, таким образом появляется чистый направленный импульс к центру объекта A (P3). Если принять это предположение, то отражённые частицы в случае 2 взаимодействующих тел полностью не компенсируют экранирующий эффект из-за того, что отражённый поток слабее падающего на тело.
Обратно-квадратичная зависимость[править | править код]

Из нашего предположения, что некоторые (или все) гравитационные частицы, сходящиеся на объекте, абсорбируются или замедляются данным объектом, следует, что интенсивность потока гравитационных частиц, испускаемого от массивного объекта, меньше, чем интенсивность потока, падающего на данный объект. Можно предположить, что этот дисбаланс импульса потока и соответственно силы приложенной на любое тело вблизи объекта распределён по сферической поверхности с центром на данном объекте (P4). Дисбаланс импульса потока над всей сферической поверхностью, окружающей объект, не зависит от размера окружающей сферы, в то же время площадь поверхности сферы увеличивается пропорционально квадрату радиуса. Следовательно, дисбаланс импульса на единицу площади уменьшается в обратно-квадратичной зависимости от расстояния.
Пропорциональность массе[править | править код]
Из фактов, показанных выше, возникает сила, которая прямо пропорциональна только площади поверхности тела. Но сила гравитации пропорциональна также массам. Чтобы удовлетворить необходимость в пропорциональности от массы, теория утверждает, что: а) базовые элементы материи очень малы; таким образом, материя в основном состоит из пустого пространства; б) что гравитационные частицы настолько малы, что только очень малая часть из них перехватывается материей. В результате чего «тень» каждого тела прямо пропорциональна поверхности каждого из базовых элементов материи. Если теперь предположить, что элементарные непрозрачные (для гравитационных частиц) элементы всей материи идентичны (т.е. имеют такое же отношение плотности к поверхности), то из этого следует, что экранирующий эффект (хотя бы приблизительно) пропорционален массе (P5).

Раннее развитие теории[править | править код]
Фатио[править | править код]
Фатио представил первую формулировку своих мыслей о гравитации в письме к Гюйгенсу весной 1690 года[1]. Два дня спустя он зачитал содержание письма перед Лондонским Королевским обществом. В последующие годы Фатио написал несколько черновых рукописей своего главного труда «De la Cause de la Pesanteur». Некоторые фрагменты этих рукописей были в последующем приобретены Ле Сажем (см. ниже) и были найдены разбросанными среди бумаг Ле Сажа в 1944 году. На основании этих фрагментов и конспекта, сделанного самим Фатио, Бернар Ганьебен попытался восстановить труды Фатио[6]. Ганьебен не знал, что полная копия одного из ранних черновиков, написанных в 1701 году, была найдена Карлом Боппом в 1915 году среди бумаг семьи Бернулли и легла в основу издания труда Фатио, опубликованного Боппом в 1929 году[7]. Издание Боппа более подробное, чем издание Ганьебена, но издание Ганьебена включает в себя исправления, сделанные Фатио до 1743 года включительно, на 40 лет позже создания черновика, на котором основывается издание Боппа. Для детального анализа труда Фатио и сравнения между изданиями Боппа и Ганьебена смотрите публикации Цехе[8]. Ниже приведённое описание в основном основано на издании Боппа. Они были названы Фатио «Проблемами I-IV», в то же время между Проблемой I и проблемой II формулируется 5 теорем. Проблемы II-IV составляют вторую половину издания Боппа и содержат математически наиболее передовые идеи теории Фатио, но они не были включены Ганьебеном в его издание трудов Фатио.
Некоторые свойства теории Фатио.[править | править код]
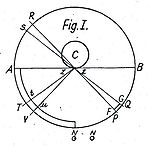
Пирамида Фатио (Проблема I)[9]: Фатио предположил, что вселенная наполнена мельчайшими корпускулами, которые движутся с очень высокой скоростью беспорядочно и прямолинейно во всех направлениях. Чтобы проиллюстрировать свои мысли, он использовал следующий пример: Вообразим объект С, на котором расположена бесконечно маленькая плоскость zz и нарисована сфера с центром в zz. В эту сферу Фатио поместил пирамиду PzzQ, в которой некоторые корпускулы движутся в направлении zz, а также некоторые корпускулы, которые уже были отражены объектом C и, следовательно, покидают плоскость zz. Фатио предположил, что средняя скорость отражённых частиц меньше, и следовательно импульс слабее, чем у падающих на тело корпускул. В результате получается один поток, который толкает все тела по направлению к zz. Таким образом, с одной стороны скорость потока остаётся постоянной, но с другой стороны при большей близости к zz плотность потока увеличивается и следовательно его интенсивность пропорциональна 1/r2. А так как можно нарисовать бесконечное количество таких пирамид вокруг C, пропорциональность 1/r2 приложима ко всей области вокруг C.
Уменьшенная скорость: чтобы подтвердить предположение, что корпускулы после отражения движутся с уменьшенными скоростями, Фатио сделал следующие предположения[10]: a) обыкновенное вещество, или гравитационные корпускулы или и то и другое неупруги; b) столкновения полностью упруги, но корпускулы не абсолютно твёрдые и следовательно переходят в состояние колебания после соударения и(или) c) из-за трения корпускулы начинают вращаться после столкновения. Эти отрывки теории Фатио наиболее малопонятны, потому что он никогда точно не решил, какой из вариантов столкновений наиболее предпочтителен[11]. Однако в последней версии своей теории в 1742 году он сократил связанные отрывки и написал «полная упругость или пружинистая сила» для корпускул и «неполная упругость» для обыкновенного вещества, следовательно корпускулы должны быть отражены с уменьшенными скоростями[12].
Вдобавок Фатио столкнулся с другой проблемой: что происходит, когда корпускулы сталкиваются друг с другом? Неупругое столкновение приводит к постоянному уменьшению скорости корпускул и следовательно к уменьшению гравитационной силы. Чтобы избежать данной проблемы, Фатио предположил, что диаметр корпускул очень мал по сравнению с расстоянием между ними, таким образом взаимодействия между корпускулами происходят очень редко.
Конденсация[13]: чтобы смягчить противоречия, которые возникли из-за того, что чем меньше скорость корпускул, тем больше корпускул будет аккумулироваться около тел, Фатио предположил, что корпускулы отражаются в пирамиду TzzV. В то же время, если корпускулы приходящие со стороны PQ достигают C, то отражённые частицы не достигают TV, а прибывают в tu. Однако это не приводит к бесконечному накоплению частиц, а только к конденсации, т.к. увеличенная плотность остаётся постоянной. Фатио указал на то, что, продолжая увеличивать скорость, Tt может стать сколько угодно малым по отношению к TZ.

Пористость обыкновенного вещества[14]: чтобы обеспечить пропорциональность массе, Фатио предположил, что обыкновенное вещество чрезвычайно проницаемо для гравитационной жидкости (потока корпускул). Он сделал наброски 3 моделей, чтобы подтвердить своё предположение. a) Фатио предположил, что материя состоит из маленьких «шариков», диаметр которых по сравнению с расстоянием между ними «бесконечно» мал. Но он отбросил данное предположение, на основании того, что при таких условиях «шарики» будут стремиться друг к другу, и тело не будет оставаться «стабильным». b) После этого он сделал предположение, что «шарики» могут быть соединены линиями или прутьями, и формируют в некотором роде кристаллическую решётку. Однако он признал негодной и эту модель тоже. Если некоторые атомы находятся рядом друг с другом, то гравитационная жидкость не сможет проникнуть в эту структуру одинаково со всех сторон, и соответственно пропорциональность массе невозможна. c) В конце концов, Фатио убрал и «шарики», оставив только линии или сетку, сделав линии «бесконечно» меньшими по сравнению с расстоянием между ними, достигнув таким образом максимальной проницательной способности.
Сила давления корпускул (Проблема II)[15]: Уже в 1690 году Фатио предположил, что «толкающая сила», вызываемая корпускулами на ровной плоскости, в 6 раз меньше, чем сила, которая была бы создана этими же корпускулами, если бы они были расположены по нормали к поверхности. Фатио приводит доказательство своего предположения путём определения силы, которая вызывается корпускулами на определённой точки плоскости zz. Он выводит формулу p=ρv²zz/6. Это решение очень похоже на формулу, известную в кинетической теории газов p=ρv²/3, которая была найдена Даниилом Бернулли в 1738 году. Это первый раз, когда наблюдается близкая аналогия между таким видом гравитационных теорий и кинетической теорией газов – задолго до развития базовых концепций более поздней из теорий. Однако значение, полученное Бернулли, в 2 раза больше, чем значение Фатио, потому что (по Цехе) Фатио рассчитал только значение mv для изменения импульса после столкновения, а не 2mv и, следовательно, получил неправильный результат (его результат верен только для полностью неупругого столкновения). Фатио пытался использовать своё решение не только для объяснения гравитации, но также и для объяснения поведения газов. Он попытался сконструировать термометр, который должен был показывать «состояние движения» молекул воздуха и, следовательно, подсчитывать температуру. Но Фатио (в отличие от Бернулли) не идентифицировал теплоту с движением частиц воздуха, он использовал другую жидкость, которая должна быть ответственна за этот эффект[16]. Также не известно, оказали ли труды Фатио влияние на Бернулли или нет.
Бесконечность (Проблема III)[17]: В этой главе Фатио исследует связь между понятием «бесконечность» и её отношением к своей теории. Фатио часто объяснял свои предположения тем фактом, что различные явления «бесконечно меньше или бесконечно больше» чем другие, и таким образом многие проблемы могут быть уменьшены до неопределяемого значения. Например, диаметр «переборок» «бесконечно меньше», чем расстояние между ними или что скорость корпускул «бесконечно больше», чем у обыкновенного вещества или разница в скорости между отражёнными или неотражёнными корпускулами «бесконечно маленькая».
Сопротивление среды (Проблема IV)[18]: Это математически самая сложная часть теории Фатио. Здесь он пытается оценить сопротивление потока корпускул движущемуся телу. Предположим, что u – скорость обыкновенного вещества, v – скорость гравитационных частиц и ρ – плотность среды. В случае если v << u и ρ = const, Фатио сделал вывод что сопротивление равно ρu2. В случае если v >> u и ρ = const, сопротивление равно 4/3ρuv. В этом месте Ньютон констатировал, что отсутствие сопротивления орбитальному движению планет требует чрезвычайную разрежённость любой среды в космосе. Поэтому Фатио уменьшил плотность среды и заявил, что, чтобы сохранить достаточную гравитационную силу, это уменьшение должно быть компенсировано изменением v «обратно пропорционально квадратному корню плотности». Это следует из корпускулярного давления Фатио, которое пропорционально ρv2. Согласно Цехе, идея Фатио увеличить v до очень больших значений действительно сделает сопротивление очень маленьким по сравнению с гравитацией (и вообще сколь угодно маленьким) из-за того, что сопротивление в модели Фатио пропорционально ρuv, а гравитация (т.е. давление корпускул) пропорциональна ρv2.
Принятие теории Фатио научным сообществом[править | править код]
Фатио контактировал с некоторыми из самых известных учёных своего времени; отдельные из них подписали его рукопись.

Мнения Ньютона о теории Фатио сильно различаются. Например, после описания необходимых условий механического объяснения гравитации, в 1692 году он написал в (неопубликованной) записке в своей собственной копии «Principia»:
Уникальная гипотеза, которая может объяснить гравитацию, была разработана самым гениальным геометром мистером Н. Фатио[19].
С другой стороны, сам Фатио заявлял, что, хотя Ньютон лично прокомментировал, что теория Фатио является самым лучшим возможным механическим объяснением гравитации, он также признавал, что Ньютон склонялся к идее, что действительная причина тяготения не является механической. Также Д. Грегори сделал заметку в своей «Memoranda» «Мистер Ньютон и мистер Галлей смеялись над манерой изложения гравитации Фатио». Это якобы было замечено им 28 декабря 1691 года. Однако настоящая дата неизвестна, так как и чернила и перо, которые использовались, отличаются от остальной части страницы[20]. После 1694 года отношения между двумя учёными охладели.
Гюйгенс был первым человеком, проинформированным Фатио о своей теории, но он никогда не признавал теорию верной. Фатио верил, что убедил Гюйгенса в состоятельности своей теории, но Гюйгенс опроверг это в своём письме к Лейбницу[21]. Также существовала короткая переписка о теории между Фатио и Лейбницем. Лейбниц критиковал теорию Фатио за существование пустого пространства между частицами, существование которого отрицалось Лейбницем на философской почве[22]. Якоб Бернулли проявил интерес к теории Фатио и побудил Фатио записать свои мысли о гравитации в законченной рукописи, что и было сделано Фатио. Бернулли после этого скопировал рукопись, которая теперь находится в библиотеке университета Базеля, и на которой основано издание Боппа[23].
Тем не менее, теория Фатио оставалась в основном неизвестной (кроме некоторых исключений, например Крамера и Лесажа) из-за того, что a) он никогда не смог формально опубликовать свои работы и b) он попал под влияние группы религиозных фанатиков, называвшейся «Французские пророки» («French prophets»), принадлежавшей к французскому протестантскому течению камизаров (camisards), поднявшему восстание против религиозных преследований во Франции в этот исторический период, и его публичная репутация была подорвана.
Крамер, Редекер[править | править код]
В 1731 году швейцарский математик Габриель Крамер опубликовал диссертацию[24], в конце которой появился набросок теории, абсолютно похожей на теорию Фатио (включая «сетевидную» структуру вещества, аналогию со светом, экранирование и т.д.), но без упоминания имени Фатио. Фатио было известно, что Крамер имел доступ к копии его главной работы, так что он обвинил Крамера в плагиате теории без понимания её. Крамер также проинформировал Лесажа о теории Фатио в 1749 году. В 1736 году германский врач Редекер тоже публикует похожую теорию[25]. В соответствии с Превостом, Редекер предположил, что частицы в его модели абсолютно неупруги, но не дал точный анализ феномена. Существовала ли связь между Фатио и Редекером – неизвестно[26].
Ле Саж[править | править код]
Первое описание своей теории Essai sur l'origine des forces mortes, было отправлено Лесажем в Парижскую Академию наук в 1748 году, но оно никогда не было опубликовано (с. 154-158). Так, по словам Лесажа, после создания и отправки своего эссе, он был проинформирован о теориях Фатио, Крамера и Редекера. Только в 1756 году в первый раз одно из описаний его теории было опубликовано[27], в 1758 году он отправил более детальное описание теории Essai de Chymie Méchanique, на конкурс в Академию наук Руана[28]. В этом труде он пытался объяснить как природу гравитации, так и силы химического притяжения. Описание теории, которое стало доступным широкой публике называлось Lucrèce Newtonien, в этом описании было раскрыто соответствие данной теории с представлениями Лукреция[29]. Ещё одно описание теории из записок Лесажа было опубликовано после смерти автора в 1818 году Пьером Прево[30].
Критика[править | править код]
Критики теории Лесажа отмечали множество её слабых мест, особенно с точки зрения термодинамики. Джеймс Максвелл показал, что в модели Лесажа энергия непременно перейдёт в теплоту и быстро расплавит любое тело. Анри Пуанкаре подсчитал (1908), что скорость корпускул должна быть на много порядков выше скорости света, и их энергия испепелила бы все планеты[31]. Были отмечены и непреодолимые логические трудности[32]:
- Если тяготение вызвано экранированием, то Луна в те моменты, когда она находится между Землёй и Солнцем, должна существенно влиять на силу притяжения этих тел и, соответственно, на траекторию Земли, однако ничего подобного в реальности не наблюдается.
- Быстро движущееся тело должно испытывать спереди избыточное давление со стороны корпускул.
Попытка Джорджа Дарвина заменить корпускулы на волны в эфире оказалась также неудачной. В обзоре 1910 года модель Лесажа уверенно характеризуется как несостоятельная[31].
См. также[править | править код]
Литература[править | править код]
- Богородский А. Ф. Всемирное тяготения. — Киев: Наукова думка, 1971. — 351 с.
- Роузвер Н. Т. Перигелий Меркурия. От Леверье до Эйнштейна = Mercury's perihelion. From Le Verrier to Einstein. — М.: Мир, 1985. — 244 с.
Примечания[править | править код]
- ↑ 1 2 Fatio, 1690a
- ↑ Le Sage, 1756
- ↑ Thomson, W. 1873
- ↑ Maxwell и 1875
- ↑ Poincaré, 1908
- ↑ Fatio, 1743
- ↑ Fatio, 1701
- ↑ Zehe, 1980
- ↑ Fatio, 1690a; Fatio, 1701, pp. 32-35; Zehe, 1980, pp. 134-156
- ↑ Fatio, 1690a; Fatio, 1701, p. 34;
- ↑ Zehe, 1980, pp. 198-204.
- ↑ Zehe, 1980, p. 385; Fatio, 1743, pp. 134-135.
- ↑ Fatio, 1690a, p. 387; Fatio, 1690c, pp. 38-39;
- ↑ Fatio, 1701, pp. 36-38 and 59-61; Zehe, 1980, pp. 206-214.
- ↑ Fatio, 1701, pp. 47-49; Zehe, 1980, pp. 227-241 and 198-205
- ↑ Zehe, 1980, p. 239
- ↑ Fatio, 1701, pp. 49-50; Zehe, 1980, pp. 242-254.
- ↑ Fatio, 1701, pp. 50-64. Zehe, 1980, pp. 255-276.
- ↑ Newton, in Latin:«Hiijus autem generis Hypothesis est unica, per quam Gravitas explicari potest, eamque Geometra Ingeniossimus Pr. Fatius primus excogitavit.»; Fatio-c, p. 65;
- ↑ Zehe, 1980, p. 374.
- ↑ Zehe, 1980, p. 176
- ↑ Zehe, 1980, pp. 173—175
- ↑ Fatio, 1701, pp. 19-20
- ↑ Cramer, 1731
- ↑ Redeker, 1736
- ↑ Le Sage, 1818, pp. XXXI-XXXII
- ↑ Le Sage, G.-L. (1756), "Letter à une académicien de Dijon...", Mercure de France: 153–171
{{citation}}: Неизвестный параметр|author-name=игнорируется (справка) - ↑ Le Sage, G.-L. (1761), Essai de Chymie Méchanique, Not published - private print Архивная копия от 5 декабря 2020 на Wayback Machine
- ↑ Le Sage, G.-L. (1784), "Lucrèce Newtonien", Memoires de l’Academie Royale des Sciences et Belles Lettres de Berlin: 404–432 Архивная копия от 17 июня 2008 на Wayback Machine An English translation appears in Le Sage, G.-L. (1898), Langley, Samuel P. (ed.), "The Le Sage theory of gravitation", Annual Report of the Board of Regents of the Smithsonian Institution (published June 30, 1898), pp. 139–160
{{citation}}:|contribution=игнорируется (справка) Архивная копия от 6 декабря 2020 на Wayback Machine - ↑ Le Sage, G.-L. (1818), "Physique Mécanique des Georges-Louis Le Sage", in Prévost, Pierre (ed.), Deux Traites de Physique Mécanique, Geneva & Paris: J.J. Paschoud, pp. 1–186, Архивировано из оригинала 26 июня 2015 Архивная копия от 26 июня 2015 на Wayback Machine
- ↑ 1 2 Роузвер Н. Т., 1985, с. 133—138..
- ↑ Богородский А. Ф., 1971, с. 31—34.