Задача коммивояжёра

Задача коммивояжёра (или TSP от англ. travelling salesman problem) — одна из самых известных задач комбинаторной оптимизации, заключающаяся в поиске самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с последующим возвратом в исходный город. В условиях задачи указываются критерий выгодности маршрута (кратчайший, самый дешёвый, совокупный критерий и тому подобное) и соответствующие матрицы расстояний, стоимости и тому подобного. Как правило, указывается, что маршрут должен проходить через каждый город только один раз — в таком случае выбор осуществляется среди гамильтоновых циклов. Существует несколько частных случаев общей постановки задачи, в частности, геометрическая задача коммивояжёра (также называемая планарной или евклидовой, когда матрица расстояний отражает расстояния между точками на плоскости), метрическая задача коммивояжёра (когда на матрице стоимостей выполняется неравенство треугольника), симметричная и асимметричная задачи коммивояжёра. Также существует обобщение задачи, так называемая обобщённая задача коммивояжёра.
Оптимизационная постановка задачи относится к классу NP-трудных задач, впрочем, как и большинство её частных случаев. Версия «decision problem» (то есть такая, в которой ставится вопрос, существует ли маршрут не длиннее, чем заданное значение k) относится к классу NP-полных задач. Задача коммивояжёра относится к числу трансвычислительных: уже при относительно небольшом числе городов (>66) она не может быть решена методом перебора вариантов никакими теоретически мыслимыми компьютерами за время, меньшее нескольких миллиардов лет.
История[править | править код]
С задачей коммивояжёра связана задача о поиске гамильтонового цикла. Примером такой задачи является задача о ходе коня, известная по крайней мере с XVIII века[1]. Леонард Эйлер посвятил ей большую работу «Решение одного любопытного вопроса, который, кажется, не подчиняется никакому исследованию», датированную 1759 годом[2]. Другим примером задачи на поиск гамильтонового цикла является икосиан: математическая головомка, в которой надо пройти по додекаэдру (графу с 20 узлами) побывав в каждой вершине ровно один раз. Эта задача была предложена Уильямом Гамильтоном в XIX веке, он же определил класс таких путей.
В 1832 году издана книга с названием «Коммивояжёр — как он должен вести себя и что должен делать для того, чтобы доставлять товар и иметь успех в своих делах — советы старого курьера» (нем. Der Handlungsreisende – wie er sein soll und was er zu tun hat, um Aufträge zu erhalten und eines glücklichen Erfolgs in seinen Geschäften gewiß zu sein – von einem alten Commis-Voyageur), в которой описана задача, но математический аппарат для её решения не применяется. Зато в ней предложены примеры маршрутов для некоторых регионов Германии и Швейцарии.
Первые упоминания в качестве математической задачи на оптимизацию принадлежат Карлу Менгеру, который сформулировал её на математическом коллоквиуме в 1930 году так:
Мы называем задачей посыльного (поскольку этот вопрос возникает у каждого почтальона, в частности, её решают многие путешественники) задачу найти кратчайший путь между конечным множеством мест, расстояние между которыми известно.
Вскоре появилось известное сейчас название задача странствующего торговца (англ. traveling salesman problem), которую предложил Хасслер Уитни (англ. Hassler Whitney) из Принстонского университета.
Вместе с простотой определения и сравнительной простотой нахождения хороших решений задача коммивояжёра отличается тем, что нахождение действительно оптимального пути является достаточно сложной задачей. Учитывая эти свойства, начиная со второй половины XX века исследование задачи коммивояжёра имеет не столько практический смысл, сколько теоретический в качестве модели для разработки новых алгоритмов оптимизации.
Многие современные распространенные методы дискретной оптимизации, такие как метод отсечений, ветвей и границ и различные варианты эвристических алгоритмов, были разработаны на примере задачи коммивояжёра.
В 1950-е и 1960-е годы задача коммивояжёра привлекла внимание ученых в США и Европе. Важный вклад в исследование задачи принадлежит Джорджу Данцигу, Делберту Рею Фалкерсону (англ. Delbert Ray Fulkerson) и Селмеру Джонсону (англ. Selmer M. Johnson), которые в 1954 году в институте RAND Corporation сформулировали задачу в виде задачи дискретной оптимизации и применили для её решения метод отсечений. Используя этот метод, они построили путь коммивояжёра для одной частной постановки задачи с 49 городами и обосновали его оптимальность. В 1960-е и 1970-е годы задача изучалась многими учеными как теоретически, так и с точки зрения её приложений в информатике, экономике, химии и биологии.
Ричард Карп в 1972 году доказал NP-полноту задачи поиска гамильтоновых путей, из чего, благодаря полиномиальной сводимости, вытекала NP-трудность задачи коммивояжёра. На основе этих свойств им было приведено теоретическое обоснование сложности поиска решений задачи на практике.
Больших успехов удалось достичь в конце 1970-х и 1980-х годах, когда Мартин Грётчел (нем. Martin Grötschel), Манфред Падберг (нем. Manfred Padberg) и Джованни Ринальди (итал. Giovanni Rinaldi) и другие, с применением новых методов деления плоскостью, ветвей и границ вычислили решение для отдельного случая задачи с 2393 городами.
В 1990-е годы Дэвид Аплгейт (англ. David Applegate), Роберт Биксби (англ. Robert Bixby), Вашек Хватал (чеш. Vašek Chvátal) и Уильям Кук (англ. William Cook) установили рекорды по программе Конкорд. Герхард Райнельт (нем. Gerhard Reinelt) создал TSPLIB — набор стандартизованных экземпляров задачи коммивояжёра различной степени сложности для сравнения результатов работы различных групп исследователей. В марте 2005 года задача с 33 810 узлами была решена программой Конкорд: был вычислен путь длиной в 66 048 945 и доказано отсутствие более коротких путей. В апреле 2006 было найдено решение для экземпляра с 85 900 узлами. Используя методы декомпозиции, можно вычислить решения для случаев задачи с миллионами узлов, длина которых менее, чем на 1 % больше оптимальной.
Формальное определение[править | править код]
Представление в виде графа[править | править код]
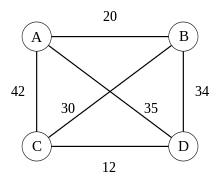
Для возможности применения математического аппарата для решения задачи её следует представить в виде математической модели. Задачу коммивояжёра можно представить в виде модели на графе, то есть, используя вершины и ребра между ними. Таким образом, вершины графа соответствуют городам, а рёбра между вершинами и — пути сообщения между этими городами. Каждому ребру можно сопоставить критерий выгодности маршрута , который можно понимать как, например, расстояние между городами, время или стоимость поездки.
Гамильтоновым циклом называется маршрут, включающий ровно по одному разу каждую вершину графа.
В целях упрощения задачи и гарантии существования маршрута обычно считается, что модельный граф задачи является полностью связным, то есть, что между произвольной парой вершин существует ребро. В тех случаях, когда между отдельными городами не существует сообщения, этого можно достичь путём ввода рёбер с максимальной длиной. Из-за большой длины такое ребро никогда не попадет в оптимальный маршрут, если он существует.
Таким образом, решение задачи коммивояжёра — это нахождение гамильтонова цикла минимального веса в полном взвешенном графе.
В зависимости от того, какой критерий выгодности маршрута сопоставляется величине ребер, различают различные варианты задачи, важнейшими из которых являются симметричная и метрическая задачи.
Асимметричная и симметричная задачи[править | править код]
В общем случае, асимметричная задача коммивояжёра отличается тем, что она моделируется ориентированным графом. Таким образом, следует также учитывать, в каком направлении находятся ребра.
В случае симметричной задачи все пары ребер между одними и теми же вершинами имеют одинаковую длину, то есть, для ребра одинаковы длины . В симметричном случае количество возможных маршрутов вдвое меньше асимметричного случая. Симметричная задача моделируется неориентированным графом (см. рисунок).
На самом деле, задача коммивояжёра в случае реальных городов может быть как симметричной, так и асимметричной в зависимости от длительности или длины маршрутов и от направления движения.
Метрическая задача[править | править код]
Симметричную задачу коммивояжёра называют метрической, если относительно длин ребер выполняется неравенство треугольника. Условно говоря, в таких задачах обходные пути длиннее прямых, то есть ребро от вершины до вершины никогда не бывает длиннее пути через промежуточную вершину :
- .
Такое свойство длины ребер определяет измеримое пространство на множестве ребер и меру расстояния, удовлетворяющую интуитивному пониманию расстояния.
Распространенные на практике функции расстояния являются также метриками и удовлетворяют неравенству треугольника:
- Евклидово расстояние в евклидовой задаче коммивояжёра,
- Манхэттенская метрика (также квартальная метрика) прямоугольной задачи коммивояжёра, в которой расстояние между вершинами на решетке равно сумме расстояний по оси ординат и абсцисс,
- Максимальная метрика, определяющая расстояние между вершинами решетчатого графа как максимальное значение расстояния вдоль оси ординат и абсцисс.
Две последние метрики находят применение, например, при сверлении отверстий в печатных платах, когда станок должен сделать больше отверстий за наименьшее время и может перемещать сверло в обоих направлениях для перехода от одного отверстия к следующему. Манхэттенская метрика соответствует случаю, когда передвижение в обоих направлениях происходит последовательно, а максимальная — случаю, когда передвижение в обоих направлениях происходит синхронно, а общее время равно максимальному времени передвижения вдоль оси ординат или абсцисс.
Неметрическая задача коммивояжёра может возникать, например, в случае минимизации длительности пребывания при наличии выбора транспортных средств в различных направлениях. В таком случае обходной путь самолетом может быть короче прямого сообщения автомобилем.
Если на практике в условиях задачи разрешается посещать города несколько раз, то симметричную задачу можно свести к метрической. Для этого задачу рассматривают на так называемом графе расстояний. Этот граф имеет такое же множество вершин, как и исходный, и является полностью связным. Длина рёбер между вершинами и на графе расстояний соответствует длине кратчайшего расстояния между вершинами и в исходном графе. Для определенных таким образом длин выполняется неравенство треугольника, и каждому маршруту на графе расстояний всегда соответствует маршрут с возможными повторениями вершин в исходном графе.
Формулировка в виде задачи дискретной оптимизации[править | править код]
Одним из подходов к решению задачи является формулировка её в виде задачи дискретной оптимизации, при этом решения представляются в виде переменных, а связи — в виде отношений неравенства между ними. Таким образом, возможно несколько вариантов. Например, симметричную задачу можно представить в виде множества ребер . Каждому ребру сопоставляется двоичная переменная , равная 1, если ребро принадлежит маршруту, и 0 — в противном случае. Произвольный маршрут можно представить в виде значений множества переменных принадлежности, но не каждое такое множество определяет маршрут. Условием того, что значения множества переменных определяют маршрут, являются описанные далее линейные неравенства.

Каждая вершина должна сообщаться через пару ребер с остальным вершинам, то есть, через входное и выходное ребро:
В сумме каждое слагаемое равно или 1 (принадлежит маршруту) или 0 (не принадлежит). То есть, полученная сумма равна количеству ребер в маршруте, имеющих вершину на одном из концов. Она равна 2, так как каждая вершина имеет входное и выходное ребро. В приведенном рядом рисунке вершина показана с входным и выходными ребрами, а ребра маршрута обозначены толстыми линиями. Рядом с ребрами указаны длины , прилагаемые к указанной выше сумме.

Описанные ранее условия кратности выполняются не только маршрутами, но и значениями переменных, соответствующих отдельным циклам, где каждая вершина принадлежит лишь одному циклу (см. рисунок). Чтобы избежать подобных случаев, должны выполняться так называемые неравенства циклов (или условия устранения подмаршрутов), которые были определены Данцигом, Фалкерсоном и Джонсоном в 1954 году под названием условия петель (англ. loop conditions). Этими неравенствами определялось дополнительное условие того, что каждое множество вершин является либо пустым, либо содержит все вершины, сочетающееся с остальным вершинам через минимум два ребра:
для всех множеств вершин , где . Эта сумма равна сумме длин ребер маршрута между вершиной и вершиной . Чтобы устранить лишние неравенства, можно ограничиться множествами вершин с минимум двумя и максимум вершинами. На рисунке рядом ребра с длинами обозначены толстыми линиями, остальные ребра имеют длину . Введение дополнительных условий (2) для множества вершин , состоящего из трех левых вершин, будет гарантировать, что сочетается через минимум два ребра маршрута с тремя вершинами справа, чтобы устранить оба цикла. Количество неравенств устранения циклов согласно Данцигу, Фалкерсону и Джонсону равняется .
В 1960 году Миллер, Такер и Землин изобрели альтернативные условия устранения подмаршрутов путём введения новых переменных, определяющих порядок посещенных городов, требующих только дополнительных неравенств. Более того, из-за двойственности в формулировках Миллера, Такера и Землина задача коммивояжёра остается NP-сложной.
Так, каждый вектор с элементами, равными 0 и 1, удовлетворяющий всем неравенствам, определяет корректный маршрут, который является решением переформулированной задачи коммивояжёра: вычислить
Поскольку переменные имеют значения только 0 и 1, сумма равна общей длине ребер , принадлежащих маршруту.
Количество неравенств типа (2) растет экспоненциально по мере увеличения количества городов, поскольку почти каждое из подмножеств узлов определяет одно неравенство. Эту задачу можно решить применением метода отсечения плоскостью, благодаря которому неравенства добавляются, только когда эти неравенства действительно необходимы. С геометрической точки зрения, линейные неравенства можно представить как гиперплоскости в пространстве переменных. Множество векторов, удовлетворяющих этим неравенствам, образуют в таком пространстве политоп (многомерный многогранник), или многомерный многоугольник, точная форма определяется длинами и является в основном неизвестной. Однако, можно показать, что условия (1) и (2) определяют грани (фацет) политопа, то есть боковые поверхности политопа с наивысшей размерностью. Поэтому они относятся к самым сильным линейным неравенствам, которые могут описывать маршрут. Также существует много разных граней, определяемых неравенствами, известными лишь в немногих случаях. Хотя (1) и (2) вместе с ограничениями полностью моделируют задачу только для двоичных векторов, эти неравенства могут использоваться в методе ветвей и границ, чтобы отбросить решения методами линейной оптимизации с нецелыми координатами (см. раздел точные методы ниже).
Алгоритмическая сложность[править | править код]
Поскольку коммивояжёр в каждом из городов встает перед выбором следующего города из тех, что он ещё не посетил, существует маршрутов для асимметричной и маршрутов для симметричной задачи коммивояжёра. Таким образом, размер пространства поиска факториально зависит от количества городов.
Различные варианты задачи коммивояжёра (метрическая, симметричная и асимметричная) NP-эквивалентны. Согласно распространенной, но недоказанной гипотезе о неравенстве классов сложности P и NP, не существует детерминированной машины Тьюринга, способной находить решения экземпляров задачи за полиномиальное время в зависимости от количества городов.
Также известно, что при условии не существует алгоритма, который для некоторого полинома вычислял бы такие решения задачи коммивояжёра, которые отличались бы от оптимального максимум на коэффициент .
На практике поиск строго оптимального маршрута требуется не всегда. Существуют алгоритмы поиска приближенных решений для метрической задачи за полиномиальное время и нахождения маршрута максимум вдвое длиннее оптимального. До сих пор не известен ни один алгоритм с полиномиальным временем, который бы гарантировал точность лучшую, чем 1,5 от оптимальной. По предположению , существует (неизвестная) константа , такая, что ни один алгоритм с полиномиальным временем не может гарантировать точность . Как было показано Арора, для евклидовой задачи коммивояжёра существует схема полиномиального времени PTAS для поиска приближённого решения.
Кроме того данные могут иметь особенности, которые могут помочь решить задачу. Например, города расположены не случайно, а по рельефу местности, либо даже вдоль уже давно найденного оптимального торгового маршрута. Дополнительная информация и эвристики позволяют за приемлемое время находить приемлемые решения.
Замкнутый и незамкнутый варианты задачи[править | править код]
В замкнутом варианте задачи коммивояжёра требуется посетить все вершины графа, после чего вернуться в исходную вершину. Незамкнутый вариант отличается от замкнутого тем, что в нём не требуется возвращаться в стартовую вершину.
Незамкнутый вариант задачи сводится к замкнутому путём замены весов дуг, входящих в стартовую вершину, на число 0. Оптимальный замкнутый маршрут коммивояжёра в таком графе соответствует оптимальному незамкнутому маршруту в исходном графе.
Чтобы свести замкнутый вариант к незамкнутому, нужно определить число , строго превосходящее вес любого маршрута коммивояжёра в заданном графе (например, в качестве можно взять сумму максимальных по весу дуг, выходящих из каждой вершины, увеличенную на 1). Затем нужно добавить к графу новую вершину (предполагаем, что вершины исходного графа пронумерованы числами от 0 до , при этом стартовая вершина имеет номер 0). Стоимости дуг, выходящих и входящих в вершину , определяются следующим образом:
- при от до
Оптимальный незамкнутый маршрут коммивояжёра в таком графе соответствует оптимальному замкнутому маршруту коммивояжёра в исходном графе и имеет стоимость на больше.
Методы решения[править | править код]
Простейшие[править | править код]
- полный перебор
- случайный перебор
- жадные алгоритмы
- метод минимального остовного дерева
- метод имитации отжига
Все эффективные (сокращающие полный перебор) методы решения задачи коммивояжёра — методы эвристические. Большинство эвристических методов находит не самый эффективный маршрут, а приближённое решение. Зачастую востребованы так называемые any-time-алгоритмы[уточнить], то есть, постепенно улучшающие некоторое текущее приближенное решение.
Примером простейшего метода решения метрического варианта задачи является использование минимальных остовных деревьев, дающее решение с фактором аппроксимации и имеющее временную сложность . Идея заключается в том, что каждый связный граф содержит нижний порог стоимости его подграфа - минимальное остовное дерево, и в том, что любой цикл, посещающий каждую вершину графа минимум один раз, может быть трансформирован в оптимальный с точки зрения стоимости маршрут при использовании метрики:
- Найди минимальное остовное дерево графа .
- Создай граф , удвоив все рёбра в . Так все вершины в имеют чётное количество рёбер.
- Найди в эйлеров цикл .
- Сократи , пропуская удвоенные рёбра, получив цикл .
- Выведи .
Значение фактора аппроксимации доказывается следующим образом: Пусть - минимальное остовное дерево, - то же дерево, но с удвоенными рёбрами, - эйлеров цикл на графе , - результат работы алгоритма, - минимальный маршрут. Заметим, что , а также . Тогда фактор аппроксимации равен .
Однако вышеописанный метод можно оптимизировать, увеличивая число рёбер у вершин с нечётным количеством соседей на 1, что соответствует паросочетанию "нечётных" вершин. Важно заметить, что количество "нечётных" вершин всегда чётно, исходя из леммы о рукопожатиях. В таком случае оптимизированный алгоритм имеет фактор аппроксимации и временную сложность . Перед доказательством покажем, что , где - паросочетание, а - оптимальный маршрут: Пусть - множество "нечётных" вершин минимального остовного дерева , а - цикл, полученный из путем пропуска вершин . Очевидно, что имеет чётную длину, а также два непересекающихся максимальных паросочетания и , для которых справедливо и . Из этого следует, что , а значит . Исходя из этого найдем фактор аппроксимации алгоритма: .
Существуют также постановки, в которых задача коммивояжёра становится NP-полной. Обычно такие постановки выглядят следующим образом: существует ли на заданном графе G такой обход, что его стоимость не превышает x. Часто на ней проводят обкатку новых подходов к эвристическому сокращению полного перебора.
На практике применяются различные модификации более эффективных методов: метод ветвей и границ и метод генетических алгоритмов, а также алгоритм муравьиной колонии.
Метод ветвей и границ[править | править код]
Можно найти точное решение задачи коммивояжёра, то есть «вручную» вычислить длины всех возможных маршрутов и выбрать маршрут с наименьшей длиной. Однако даже для небольшого количества городов решать задачу таким способом практически невозможно. Для простого варианта, симметричной задачи с городами, существует возможных маршрутов, то есть для 15 городов существует 43 миллиарда маршрутов и для 18 городов уже 177 триллионов. То, как стремительно растет продолжительность вычислений, можно показать на следующем примере. Если бы существовало устройство, находящее решение для 30 городов за час, то для двух дополнительных городов требуется в тысячу раз больше времени; то есть, более чем 40 суток.

Методы дискретной оптимизации, в частности ветвей и границ, позволяют находить оптимальные или приблизительные решения для достаточно больших задач.
В геометрической интерпретации эти методы рассматривают задачу как выпуклый политоп, то есть многомерный многоугольник в -мерном единичном кубе , где равно количеству ребер в графе. Каждая вершина этого единичного куба соответствует маршруту, то есть вектору с элементами 0/1, что удовлетворяет описанным выше линейным неравенствам. Гиперплоскости, описываемые этими неравенствами, отсекают такие ребра единичного куба, которые не соответствуют ни одному маршруту.
На рисунке рядом показано применение метода для задачи с тремя узлами. В соответствие трем возможным ребрам между вершинами сопоставляются бинарные переменные и . В этом случае существует лишь один возможный маршрут, а именно тот, что проходит через три вершины. Этот маршрут удовлетворяет неравенству , которое утверждает, что маршрут должен проходить через минимум две вершины. Кроме этого маршрута, что соответствует вектору (1,1,1), неравенству удовлетворяют также все точки в отмеченной красным части этого неравенства. Плоскости, проходящие через красные линии, отсекают все углы, отвечающие несуществующим маршрутам с максимум одним ребром, а именно, ноль-вектор (0, 0, 0), единичные векторы (1, 0, 0), (0, 1, 0) и (0, 0, 1). Сильное неравенство отсечет от единичного куба все, кроме единственной допустимой точки (1, 1, 1). В этом отдельном случае тот же эффект можно получить тремя неравенствами типа (1).
Для определения допустимого ребра с наименьшей длиной следует решить наборы задач линейной оптимизации, отсекающие секущими плоскостями ненужные части единичного куба и попытаться разделить единичный куб на меньшие политопы методом ветвей и границ.
Однако этого метода для быстрого поиска маршрутов обычно недостаточно. Основное преимущество точных методов заключается в том, что имея достаточно времени, они вычисляют кратчайший маршрут. Имея нижнюю границу для оптимальных решений, можно оценить то, насколько отличается найденный маршрут от оптимального. Например, имея нижнюю границу на уровне 100, и после нахождения маршрута длиной 102, оптимальный маршрут может находиться в пределах от 100 до 102. Так называемый интервал оптимальности, или максимальное относительное расстояние между длиной оптимального маршрута и кратчайшим известным маршрутом составит (102—100)/100 = 2 %, то есть длина найденного маршрута 102 максимум на 2 % отличается от оптимальной. Когда длина вычисленного маршрута равна длине предыдущего, считается, что найденное решение является оптимальным. Для поиска маршрутов приемлемой длины точные методы могут комбинироваться с эвристическими.
Метод ветвей и границ для решения задачи коммивояжёра был предложен в 1963 году группой авторов (Дж. Литл, К. Мурти, Д. Суини, К. Кэрол)[3].
Метод эластичной сети[править | править код]
Эта статья или раздел нуждается в переработке. |
История[править | править код]
В 1987 году его использовали Дурбин (Durbin) и Уиллшоу (Willshaw), указавшие аналогию с механизмами установления упорядоченных нейронных связей[4].
Каждый из маршрутов коммивояжёра рассматривался как отображение окружности на плоскость (в каждый город на плоскости отображается некоторая точка этой окружности). Соседние точки на окружности должны отображаться в точки, по возможности ближайшие и на плоскости.
Алгоритм[править | править код]
Начинается с установки на плоскость небольшой окружности. Она неравномерно расширяется, становясь кольцом, проходящим практически около всех городов и устанавливая таким образом искомый маршрут. На каждую движущуюся точку кольца оказывает действие две составляющие: перемещение точки в сторону ближайшего города и смещение в сторону соседей точки на кольце так, чтобы уменьшить его длину. Город в итоге связывается с определенным участком кольца по мере расширения. По мере расширения такой эластичной сети каждый город оказывается ассоциирован с определенным участком кольца.
Вначале все города оказывают приблизительно одинаковое влияние на каждую точку маршрута. В последующем, большие расстояния становятся менее влиятельными и каждый город становится более специфичным для ближайших к нему точек кольца. Такое постепенное увеличение специфичности, которое напоминает метод обучения сети Кохонена, контролируется значением некоторого эффективного радиуса.
Дурбин и Уиллшоу показали, что для задачи с 30 городами, рассмотренной Хопфилдом и Танком, метод эластичной сети генерирует наикратчайший маршрут примерно за 1000 итераций. Для 100 городов найденный этим методом маршрут лишь на 1 % превосходил оптимальный.
Муравьиный алгоритм[править | править код]
Генетический алгоритм[править | править код]
Алгоритм динамического программирования[править | править код]
Основная идея заключается в вычислении и запоминании пути от исходного города и до каждого из остальных городов, затем суммирования этой величины с путем из каждого из остальных городов до оставшихся городов и т. д. Преимущество данного метода перед методом полного перебора заключается в существенном сокращении полного объема вычислений за счет заметного увеличения объема памяти [5].
См. также[править | править код]
Примечания[править | править код]
- ↑ Gross J. L., Yellen J. Graph theory and its applications, 2006, с. 275.
- ↑ Euler, Leonhard, Solution d’une question curieuse que ne paroit soumise à aucune analyse Архивная копия от 19 августа 2021 на Wayback Machine, Mémoires de l’académie des sciences de Berlin, 15 (1759) 1766, p. 310—337.
- ↑ Кэрел К. , Литл Д. , Мурти К. , Суини Д. АЛГОРИТМ ДЛЯ РЕШЕНИЯ ЗАДАЧИ О КОММИВОЯЖЕРЕ // Экономика и математические методы. – 1965. – T. 1. – Выпуск № 1 C. 94-107 .
- ↑ Richard Durbin, David Willshaw. An analogue approach to the travelling salesman problem using an elastic net method (англ.) // Nature. — 1987-04-22. — Vol. 326, iss. 6114. — P. 689–691. — doi:10.1038/326689a0. Архивировано 23 апреля 2016 года.
- ↑ Корбут А. А., Финкельштейн Ю. Ю. Дискретное программирование. — М., Наука, 1969. — C. 258—264
Литература[править | править код]
- Левитин А. В. Глава 3. Метод грубой силы: Задача коммивояжёра // Алгоритмы. Введение в разработку и анализ — М.: Вильямс, 2006. — С. 159—160. — 576 с. — ISBN 978-5-8459-0987-9
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1.
- В.И. Мудров. Задача о коммивояжёре. — М.: «Знание», 1969. — С. 62.
- Ежов А., Шумский С. Нейрокомпьютинг и его применения в экономике и бизнесе . — М.: МИФИ, 1998. — С. 216.
- Gross J. L., Yellen J. Graph theory and its applications. Second edition. Boca Raton—London—New York: Chapman & Hall/CRC, 2006.
Для улучшения этой статьи желательно:
|




































































![{\displaystyle [0,1]^{m}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee7ad28c4c962381ae011e67434abe5e9a8504f7)






