Двенадцатигранники
Двенадцатигра́нник — многогранник с двенадцатью гранями.
Существует несколько объёмных фигур с двенадцатью гранями.
Правильный додекаэдр[править | править код]

С древнейших времён известна фигура, у которой 12 граней — правильные пятиугольники. Такой додекаэдр — одно из пяти платоновых тел и обладает симметрией вращения пятого порядка. Однако, у этого во многих отношениях идеального многогранника есть недостаток. Дело в том, что правильными пятиугольниками нельзя без зазоров покрыть плоскость. Также додекаэдрами невозможно плотно заполнить пространство. Из этого следует невозможность существования кристаллов с осями симметрии пятого порядка и невозможность существования кристаллов в форме платонова додекаэдра. Однако, известны вирусы и белки́ в форме такого додекаэдра, с осями симметрии пятого порядка. Предполагают, что они приобрели такую форму во избежание кристаллизации.
Пентагондодекаэдр[править | править код]
Визуально очень похож на платоново тело, но имеет совсем другую симметрию — центральный вид симметрии кубической сингонии. Грани — неправильные пятиугольники, симметричные относительно плоскости, проходящей через центр фигуры. Пентагондодекаэдр это одна из простых форм кристаллов. Огранка кристаллов пентагондодекаэдром характерна, например, для пирита.
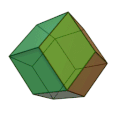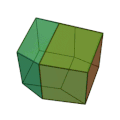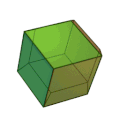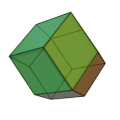
Ромбододекаэдр[править | править код]
Фигура, огранённая равными ромбами и являющаяся двойственным кубооктаэдру многогранником.
Между пентагондодекаэдром и ромбододекаэдром существует непосредственная связь. Пентагондодекаэдр получается из ромбододекаэдра, если отклонить грань ромбододекаэдра в сторону вершины. В этом смысле, пентагондодекаэдр является переходной формой между кубом и ромбододекаэдром.
-
индекс грани {10,9,0}
-
индекс грани {2,1,0}
-
индекс грани {7,1,0}
Гексагональная бипирамида[править | править код]
Фигура, получающаяся при соединении двух одинаковых правильных шестиугольных пирамид через их основания.
-
Гексагональная бипирамида



