Задача о кратчайшем пути

Кратчайший путь (A, B, D, F) между вершинами A и F в неориентированном графе без весов.

Кратчайший путь (A, C, E, D, F) между вершинами A и F во взвешенном ориентированном графе.

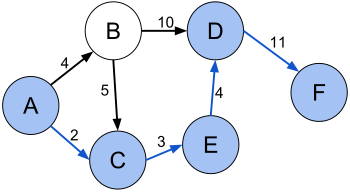
Зада́ча о кратча́йшем пути́ — задача поиска самого короткого пути (цепи) между двумя точками (вершинами) на графе, в которой минимизируется сумма весов рёбер, составляющих путь.

Задача о кратчайшем пути является одной из важнейших классических задач теории графов. Сегодня известно множество алгоритмов для её решения.

У данной задачи существуют и другие названия: задача о минимальном пути или, в устаревшем варианте, задача о дилижансе.

Значимость данной задачи определяется её различными практическими применениями. Например, в GPS-навигаторах осуществляется поиск кратчайшего пути между точкой отправления и точкой назначения. В качестве вершин выступают перекрёстки, а дороги являются рёбрами, которые лежат между ними. Если сумма длин дорог между перекрёстками минимальна, тогда найденный путь самый короткий.

Определение

Задача поиска кратчайшего пути на графе может быть определена для неориентированного, ориентированного или смешанного графа. Далее будет рассмотрена постановка задачи в самом простом виде для неориентированного графа. Для смешанного и ориентированного графа дополнительно должны учитываться направления ребер.

Граф представляет собой совокупность непустого множества вершин и рёбер (наборов пар вершин). Две вершины на графе смежны, если они соединяются общим ребром. Путь в неориентированном графе представляет собой последовательность вершин $P=(v_{1},v_{2},\ldots ,v_{n})\in V\times V\times \ldots \times V$, таких что $v_{i}$ смежна с $v_{i+1}$ для $1\leq i<n$. Такой путь $P$ называется путём длиной $n$ из вершины $v_{1}$ в $v_{n}$ ($i$ указывает на номер вершины пути и не имеет никакого отношения к нумерации вершин на графе).

Пусть $e_{i,j}$ — ребро соединяющее две вершины: $v_{i}$ и $v_{j}$. Дана весовая функция $f:E\rightarrow \mathbb {R}$, которая отображает ребра на их веса, значения которых выражаются действительными числами, и неориентированный граф $G$. Тогда кратчайшим путём из вершины $v$ в вершину $v'$ будет называться путь $P=(v_{1},v_{2},\ldots ,v_{n})$ (где $v_{1}=v$ и $v_{n}=v'$), который имеет минимальное значение суммы $\sum _{i=1}^{n-1}f(e_{i,i+1}).$ Если все ребра в графе имеют единичный вес, то задача сводится к определению наименьшего количества обходимых ребер.

Существуют различные постановки задачи о кратчайшем пути:

• Задача о кратчайшем пути в заданный пункт назначения. Требуется найти кратчайший путь в заданную вершину назначения t, который начинается в каждой из вершин графа (кроме t). Поменяв направление каждого принадлежащего графу ребра, эту задачу можно свести к задаче о единой исходной вершине (в которой осуществляется поиск кратчайшего пути из заданной вершины во все остальные).
• Задача о кратчайшем пути между заданной парой вершин. Требуется найти кратчайший путь из заданной вершины u в заданную вершину v.
• Задача о кратчайшем пути между всеми парами вершин. Требуется найти кратчайший путь из каждой вершины u в каждую вершину v. Эту задачу тоже можно решить с помощью алгоритма, предназначенного для решения задачи об одной исходной вершине, однако обычно она решается быстрее.

В различных постановках задачи, роль длины ребра могут играть не только сами длины, но и время, стоимость, расходы, объём затрачиваемых ресурсов (материальных, финансовых, топливно-энергетических и т. п.) или другие характеристики, связанные с прохождением каждого ребра. Таким образом, задача находит практическое применение в большом количестве областей (информатика, экономика, география и др.).

Задача о кратчайшем пути с учётом дополнительных ограничений

Задача о кратчайшем пути очень часто встречается в ситуации, когда необходимо учитывать дополнительные ограничения. Наличие их может значительно повысить сложность задачи. Примеры таких задач:

1. Кратчайший путь, проходящий через заданное множество вершин. Можно рассматривать два ограничения: кратчайший путь должен проходить через выделенное множество вершин, и кратчайший путь должен содержать как можно меньше невыделенных вершин. Первое из них хорошо известна в теории исследования операций.
2. Минимальное покрытие вершин ориентированного графа путями. Осуществляется поиск минимального по числу путей покрытия графа, а именно подмножества всех s-t путей, таких что, каждая вершина ориентированного графа принадлежит хотя бы одному такому пути.
3. Задача о требуемых путях. Требуется найти минимальное по мощности множество s-t путей $P={p_{1},\dots ,p_{m}}$ такое, что для любого $t_{i}\in R$ найдется путь $p_{j}\in P$, накрывающий его. $R={t_{1},\dots ,t_{k}}$ — множество некоторых путей в ориентированном графе G.
4. Минимальное покрытие дуг ориентированного графа путями. Задача состоит в отыскании минимального по числу путей подмножества всех путей, такого, что каждая дуга принадлежит хотя бы одному такому пути. При этом возможно дополнительное требование о том, чтобы все пути исходили из одной вершины.

Алгоритмы

В связи с тем, что существует множество различных постановок данной задачи, есть наиболее популярные алгоритмы для решения задачи поиска кратчайшего пути на графе:

• Алгоритм Дейкстры находит кратчайший путь от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса.
• Алгоритм Беллмана — Форда находит кратчайшие пути от одной вершины графа до всех остальных во взвешенном графе. Вес рёбер может быть отрицательным.
• Алгоритм поиска A* находит маршрут с наименьшей стоимостью от одной вершины (начальной) к другой (целевой, конечной), используя алгоритм поиска по первому наилучшему совпадению на графе.
• Алгоритм Флойда — Уоршелла находит кратчайшие пути между всеми вершинами взвешенного ориентированного графа.
• Алгоритм Джонсона находит кратчайшие пути между всеми парами вершин взвешенного ориентированного графа.
• Алгоритм Ли (волновой алгоритм) основан на методе поиска в ширину. Находит путь между вершинами s и t графа (s не совпадает с t), содержащий минимальное количество промежуточных вершин (рёбер). Основное применение — трассировки электрических соединений на кристаллах микросхем и на печатных платах. Также используется для поиска кратчайшего расстояния на карте в стратегических играх.
• Поиск кратчайшего пути на основе алгоритма Килдала.

В работе (Черкасский и др., 1993) представлено ещё несколько алгоритмов для решения этой задачи.

Задача поиска кратчайшего пути из одной вершины во все остальные

В такой постановке задачи осуществляется поиск кратчайшего пути из вершины v во все остальные вершины на графе.

Невзвешенный ориентированный граф

Алгоритм	Сложность	Автор
Поиск в ширину	O(V+E)

Это неполный список, который, возможно, никогда не будет удовлетворять определённым стандартам полноты. Вы можете дополнить его из авторитетных источников.

Ориентированный граф с неотрицательными весами

Алгоритм	Сложность	Автор
-	O(V2EL)	Форд 1956
Алгоритм Беллмана — Форда	O(VE)	Беллман 1958, Мур 1957
-	O(V2 log V)	Данциг 1958, Данциг 1960, Minty (cf. Pollack&Wiebenson 1960), Whiting&Hillier 1960
Алгоритм Дейкстры со списком.	O(V2)	Leyzorek et al. 1957, Дейкстра 1959
Алгоритм Дейкстры с модифицированной двоичной кучей	O((E + V) log V)	-
. . .	. . .	. . .
Алгоритм Дейкстры с использованием фибоначчиевой кучи	O(E + V log V)	Фридман&Тарьян 1984, Фридман&Тарьян 1987
-	O(E log log L)	Джонсон 1982, Карлссон&Поблете 1983
Алгоритм Габова	O(E logE/V L)	Габов 1983, Габов 1985
-	O(E + V√log L)	Ахуджа et al. 1990

Это неполный список, который, возможно, никогда не будет удовлетворять определённым стандартам полноты. Вы можете дополнить его из авторитетных источников.

Ориентированный граф с произвольными весами

Алгоритм	Сложность	Автор
Алгоритм Беллмана — Форда	O(VE)	Беллман, Мур
Алгоритм Левита	O(VE)

Это неполный список, который, возможно, никогда не будет удовлетворять определённым стандартам полноты. Вы можете дополнить его из авторитетных источников.

Задача о кратчайшем пути между всеми парами вершин

Задача о кратчайшем пути между всеми парами вершин для невзвешенного ориентированного графа была поставлена Симбелом в 1953 году, который обнаружил, что она может быть решена за линейное количество манипуляций (умножения) с матрицей. Сложность такого алгоритма O(V⁴).

Так же для решения данной задачи существуют другие более быстрые алгоритмы, такие как Алгоритм Флойда — Уоршелла со сложностью O(V³), и Алгоритм Джонсона (является комбинацией алгоритмов Бэллмана-Форда и Дейкстры) со сложностью O(VE + V² log V).

Применение

Задача о поиске кратчайшего пути на графе может быть интерпретирована по-разному и применяться в различных областях. Далее приведены примеры различных применений задачи. Другие применения изучаются в дисциплине, которая занимается исследованием операций.

Картографические сервисы

Алгоритмы нахождения кратчайшего пути на графе применяются для нахождения путей между физическими объектами на таких картографических сервисах, как карты Google или OpenStreetMap. В обучающем видео от Google можно узнать различные эффективные алгоритмы, которые применяются в данной сфере.

Недетерминированная машина

Если представить недетерминированную абстрактную машину как граф, где вершины описывают состояния, а ребра определяют возможные переходы, тогда алгоритмы поиска кратчайшего пути могут быть применены для поиска оптимальной последовательности решений для достижения главной цели. Например, если вершинами являются состояния Кубика Рубика, а ребром представляет собой одно действие над кубиком, тогда алгоритм может быть применён для поиска решения с минимальным количеством ходов.

Сети дорог

Задача поиска кратчайшего пути на графе широко используется при определении наименьшего расстояния в сети дорог.

Сеть дорог можно представить в виде графа с положительными весами. Вершины являются дорожными развязками, а ребра дорогами, которые их соединяют. Веса рёбер могут соответствовать протяжённости данного участка, времени необходимому для его преодоления или стоимости путешествия по нему. Ориентированные ребра можно использовать для представления односторонних улиц. В таком графе можно ввести характеристику, которая указывает на то, что одни дороги важнее других для длительных путешествий (например автомагистрали). Она была формализована в понятии (идее) о магистралях.

Для реализации подхода, где одни дороги важнее других, существует множество алгоритмов. Они решают задачу поиска кратчайшего пути намного быстрее, чем аналогичные на обычных графах. Подобные алгоритмы состоят из двух этапов:

1. этап предобработки. Производится предварительная обработка графа без учёта начальной и конечной вершины (может длиться до нескольких дней, если работать с реальными данными). Обычно выполняется один раз и потом используются полученные данные.
2. этап запроса. Осуществляется запрос и поиск кратчайшего пути, при этом известны начальная и конечная вершина.

Самый быстрый алгоритм может решить данную задачу на дорогах Европы или Америки за доли микросекунды.

Другие подходы (техники), которые применяются в данной сфере:

• ALT
• Arc Flags
• Contraction hierarchies
• Transit Node Routing
• Reach based Pruning
• Labeling

Похожие задачи

Существуют задачи, которые похожи на задачу поиска кратчайшего пути на графе.

• Поиск кратчайшего пути в вычислительной геометрии (см. евклидов кратчайший путь).
• Задача коммивояжёра. Требуется найти кратчайший маршрут, проходящий через указанные города (вершины) хотя бы по одному разу с последующим возвратом в исходный город. Данная задача относится к классу NP-трудных задач в отличие от задачи поиска кратчайшего пути, которая может быть решена за полиномиальное время в графах без циклов. Задача коммивояжёра решается неэффективно для больших наборов данных.
• Задача канадского путешественника и задача стохастического поиска кратчайшего пути являются обобщением рассматриваемой задачи, в которых обходимый граф заранее полностью неизвестен и изменяется во времени или следующий проход по графу вычисляется на основе вероятностей.
• Задача поиска кратчайшего пути, когда в графе происходят преобразования. Например, изменяется вес ребра или удаляется вершина.

Постановка задачи линейного программирования

Пусть дан направленный граф (V, A), где V — множество вершин и A — множество рёбер, с начальной вершиной обхода s, конечной t и весами w_ij для каждого ребра (i, j) в A. Вес каждого ребра соответствует переменной программы x_ij.

Тогда задача ставится следующим образом: найти минимум функции $F=\sum _{ij\in A}w_{ij}x_{ij}$, где $x_{ij}\geq 0$, при условии что для всех i и j выполняется следующее неравенство: $\sum _{j}x_{ij}-\sum _{j}x_{ji}={\begin{cases}1,&{\text{if }}i=s;\\-1,&{\text{if }}i=t;\\0,&{\text{ otherwise.}}\end{cases}}$

См. также

• IEEE 802.1aq
• Транспортная сеть
• Двунаправленный поиск

Литература

• Евстигнеев В. А. Глава 3. Итеративные алгоритмы глобального анализа графов. Пути и покрытия // [web.archive.org/web/20131212234759/publ.lib.ru/ARCHIVES/E/EVSTIGNEEV_Vladimir_Anatol'evich/_Evstigneev_V.A..html Применение теории графов в программировании] / Под ред. А. П. Ершова. — Москва: Наука. Главная редакция физико-математической литературы, 1985. — С. 138—150. — 352 с.
• Алексеев В.Е., Таланов В.А. Глава 3.4. Нахождения кратчайших путей в графе // Графы. Модели вычислений. Структуры данных. — Нижний Новгород: Издательство Нижегородского гос. университета, 2005. — С. 236—237. — 307 с. — ISBN 5–85747–810–8. Архивная копия от 13 декабря 2013 на Wayback Machine
• Галкина В.А. Глава 4. Построение кратчайших путей в ориентированном графе // Дискретная математика. Комбинаторная оптимизация на графах. — Москва: Издательство "Гелиос АРВ", 2003. — С. 75—94. — 232 с. — ISBN 5–85438–069–2.
• Берж К. Глава 7. Задача о кратчайшем пути // Теория графов и её применения = Theorie des graphes et ses applications / Под ред. И. А. Вайнштейна. — Москва: Издательство иностранной литературы, 1962. — С. 75—81. — 320 с.
• Ойстин Оре. Теория графов / Под ред. И. М. Овчинниковой. — Издательство наука, 1980. — 336 с. Архивная копия от 15 декабря 2013 на Wayback Machine
• Виталий Осипов, Поиск кратчайших путей в дорожных сетях: от теории к реализации на YouTube.
• Харари Ф. Глава 2. Графы // Теория графов / под ред. Г. П. Гаврилов — М.: Мир, 1973. — С. 27. — 301 с.
• Cherkassky B. V., Goldberg A. V., Radzik T. Shortest paths algorithms: Theory and experimental evaluation (англ.) // Mathematical Programming — Springer Science+Business Media, 1996. — Vol. 73, Iss. 2. — P. 129–174. — ISSN 0025-5610; 1436-4646 — doi:10.1007/BF02592101
• Ричард Беллман. On a routing problem // Quarterly of Applied Mathematics. — 1958. — Т. 16. — С. 87—90.
• Dijkstra E. W. A note on two problems in connexion with graphs (англ.) // Numerische Mathematik / F. Brezzi — Springer Science+Business Media, 1959. — Vol. 1, Iss. 1. — P. 269—271. — ISSN 0029-599X; 0945-3245 — doi:10.1007/BF01386390
• Moore E. F. The shortest path through a maze (англ.) // Proceedings of an International Symposium on the Theory of Switching (Cambridge, Massachusetts, 2–5 April 1957) — Harvard University Press, 1959. — Vol. 2. — P. 285—292. — 345 p. — (Annals of the Computation Laboratory of Harvard University; Vol. 30) — ISSN 0073-0750
• M. Leyzorek, R. S. Gray, A. A. Gray, W. C. Ladew, S. R. Meaker, R. M. Petry, R. N. Seitz. Investigation of Model Techniques — First Annual Report — 6 June 1956 — 1 July 1957 — A Study of Model Techniques for Communication Systems (англ.). — Cleveland, Ohio: Case Institute of Technology, 1957.
• Michael Fredman Lawrence, Роберт Андре Тарьян. Fibonacci heaps and their uses in improved network optimization algorithms (англ.) : journal. — Институт инженеров электротехники и электроники, 1984. — P. 338—346. — ISBN 0-8186-0591-X. — doi:10.1109/SFCS.1984.715934. Архивировано 11 октября 2012 года.
• Michael Fredman Lawrence, Роберт Андре Тарьян. Fibonacci heaps and their uses in improved network optimization algorithms (англ.) // Journal of the Association for Computing Machinery : journal. — 1987. — Vol. 34, no. 3. — P. 596—615. — doi:10.1145/28869.28874.
• Shimbel, Alfonso. Structural parameters of communication networks // Bulletin of Mathematical Biophysics. — 1953. — Т. 15, № 4. — С. 501—507. — doi:10.1007/BF02476438.
• Sanders, Peter. Fast route planning. — Google Tech Talk, 2009. — 23 марта.. — «Шаблон:Inconsistent citations».
• Chen, Danny Z. Developing algorithms and software for geometric path planning problems (англ.) // ACM Computing Surveys : journal. — 1996. — December (vol. 28, no. 4es). — P. 18. — doi:10.1145/242224.242246.
• Abraham, Ittai; Fiat, Amos; Goldberg, Andrew V.; Werneck, Renato F. Highway Dimension, Shortest Paths, and Provably Efficient Algorithms (англ.) // ACM-SIAM Symposium on Discrete Algorithms : journal. — 2010. — P. 782—793.
• Abraham, Ittai; Delling, Daniel; Goldberg, Andrew V.; Werneck, Renato F. A Hub-Based Labeling Algorithm for Shortest Paths on Road Networks. Symposium on Experimental Algorithms] (англ.) : journal. — 2011. — P. 230—241.
• Kroger, Martin. Shortest multiple disconnected path for the analysis of entanglements in two- and three-dimensional polymeric systems (англ.) // Computer Physics Communications : journal. — 2005. — Vol. 168, no. 168. — P. 209—232. — doi:10.1016/j.cpc.2005.01.020.
• Ladyzhensky Y., Popoff Y. Algorithm to define the shortest paths between all nodes in a graph after compressing of two nodes. Proceedings of Donetsk national technical university, Computing and automation. Vol.107. Donetsk (англ.) : journal. — 2006. — P. 68—75..