Система корней
Систе́ма корне́й (корнева́я систе́ма) в математике — конфигурация векторов в евклидовом пространстве, удовлетворяющая определённым геометрическим свойствам.
Эта концепция является фундаментальной в теории групп Ли и алгебр Ли. Диаграммы Коксетера — Дынкина, использующиеся при классификации систем корней, встречается в разделах математики, не связанных явно с группами Ли, например, в теории сингулярностей.
Определение[править | править код]
Пусть — конечномерное евклидово пространство с обычным скалярным произведением, обозначаемым . Система корней в — это конечное множество ненулевых векторов (называемых корнями), которые удовлетворяют следующим свойствам.

- является линейной оболочкой системы корней.
- Если два корня , являются коллинеарными векторами, то либо они совпадают, либо
- Для каждого корня множество замкнуто относительно отражения в гиперплоскости, перпендикулярной То есть для любых двух корней и множество содержит отражение
- (Целостное условие). Если и — корни в то проекция на прямую, проходящую через есть полуцелое, кратное То есть
Замечания[править | править код]
- С учётом свойства 3 целостное условие эквивалентно утверждению, что разность между и его отражением равна корню , умноженному на некоторое целое число.
- Оператор
- ,
- определённый свойством 4, не является внутренним произведением. Он, вообще говоря, не симметричен и линеен только по первому аргументу.
Размерность называют рангом системы корней.
Классификация систем корней по схемам Дынкина[править | править код]
Примеры систем корней ранга 1 и ранга 2[править | править код]
Существует только одна система корней ранга 1. Она состоит из двух ненулевых векторов Эта система называется
В ранге 2 существуют четыре возможных варианта где

|

|
| Система корней | Система корней |
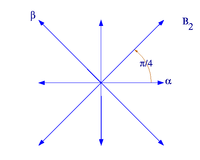
|
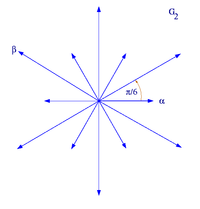
|
| Система корней | Система корней |
См. также[править | править код]
Ссылки[править | править код]
- Дынкин Е. Б. Структура полупростых алгебр Ли // Успехи математических наук. — 1947. — Т. 2, № 4(20). — С. 59–127.
- Дынкин Е. Б. Классификация простых групп Ли // Математический сборник. — 1946. — Т. 18(60), № 3. — С. 347–352.
- Хамфрис Дж. Введение в теорию алгебр Ли и их представлений / Перев. с англ. Б. Р. Френкина. — М.: МЦНМО, 2008. — 216 с.
- Винберг Э. Б., Онищик А. Л. Семинар по группам Ли и алгебраическим группам — М.: УРСС, 1995. — 344 с.
- Хамфри Дж. Линейные алгебраические группы / Пер. с англ./Под ред. В. П. Платонова. — М.: Наука, 1980. — 400 с.
- Бурбаки Н. Группы и алгебры Ли (часть 2) / Пер. с франц./Под ред. А. И. Кострикина. — М.: Мир, 1972. — 332 с.


























