Сферические функции

Сферические функции представляют собой угловую часть семейства ортогональных решений уравнения Лапласа, записанную в сферических координатах. Они широко используются для изучения физических явлений в пространственных областях, ограниченных сферическими поверхностями и при решении физических задач, обладающих сферической симметрией. Сферические функции имеют большое значение в теории дифференциальных уравнений в частных производных и теоретической физике, в частности в задачах расчёта электронных орбиталей в атоме, гравитационного поля геоида, магнитного поля планет и интенсивности реликтового излучения.
Определение[править | править код]

Сферические функции являются собственными функциями оператора Лапласа в сферической системе координат (обозначение ). Они образуют ортонормированную систему в пространстве функций на сфере в трёхмерном пространстве:
- ,
где * обозначает комплексное сопряжение, — символ Кронекера.
Сферические функции имеют вид
- ,
где функции являются решениями уравнения
и имеют вид
Здесь — присоединённые многочлены Лежандра, а — факториал.
Присоединенные многочлены Лежандра с отрицательным здесь вводятся как
Решение уравнения Лапласа в сферических координатах есть так называемая шаровая функция, получаемая умножением сферической функции на решение радиального уравнения.
Вещественная форма[править | править код]
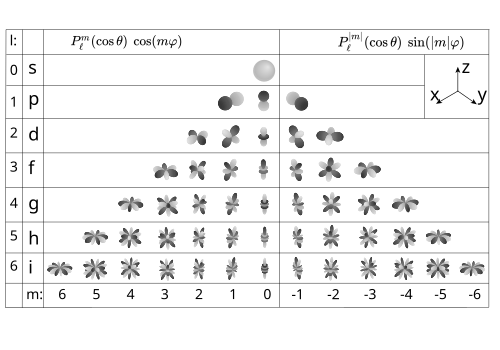
Для сферических функций форма зависимости от угла — комплексная экспонента. Используя формулу Эйлера, можно ввести вещественные сферические функции. Иногда их удобнее использовать в связи с тем, что они могут быть наглядно показаны на иллюстрациях, в отличие от комплексных. Однако значимое удобство комплексных функций (утрачиваемое при переходе к вещественным) состоит в независимости квадрата их модуля от угла .
Обратное преобразование:
Иногда вещественные сферические функции называют зональными, тессеральными и секториальными[1]. Функции с m > 0 зависят от угла как косинус, а с m < 0 — как синус.
Повороты[править | править код]

Рассмотрим поворот системы координат , на Углы Эйлера который преобрaзует единичный вектор в вектор . При этом углы вектора в новой системе координат выражаются через углы в старой системе координат следующим образом
В новой системе координат сферическая функция с индексами и будет представима в виде линейной комбинации всех функций с тем же номером и различными . Коэффициентами в линейной комбинации являются комплексно- сопряженные D-матрицы Вигнера[2]
Сферические функции с номером образуют базис неприводимого представления размерности группы вращений SO(3).
Разложение плоской волны по сферическим функциям[править | править код]
Комплексная экспонента может быть представлена в виде разложения по сферическим функциям
Здесь — сферическая функция Бесселя
Разложение произведений сферических функций[править | править код]
Разложения Клебша-Гордана для произведений двух сферических функций выглядят следующим образом [3]:
См. также[править | править код]
Примечания[править | править код]
- ↑ Тихонов А. Н., Самарский А. А. Уравнения математической физики Архивная копия от 27 декабря 2019 на Wayback Machine
- ↑ M. A. Morrison, G. A. Parker. A guide to rotations in quantum mechanics Архивная копия от 1 октября 2019 на Wayback Machine. — Australian Journal of Physics, Vol. 40, pp. 465, 1987
- ↑ Варшалович Д. А., Москалёв А. Н., Херсонский В. К. Квантовая теория углового момента. Архивная копия от 11 ноября 2007 на Wayback Machine — Л.: Наука, 1975.
Литература[править | править код]
- Ландау Л. Д., Лифшиц Е. М. Квантовая механика (нерелятивистская теория). — Издание 4-е. — М.: Наука, 1989. — 768 с. — («Теоретическая физика», том III). — ISBN 5-02-014421-5. — математические дополнения
- Пальцев Б.В. Сферические функции // Методич. матер. каф. ВМ МФТИ.
Приложения[править | править код]
- SHTOOLS: Fortran 95 software archive
- HEALPIX: Fortran 90 and C++ software archive
- SpherePack: Fortran 77 software archive
- SpharmonicKit: C software archive
- Frederik J Simons: Matlab software archive
- NFFT: C subroutine library (fast spherical Fourier transform for arbitrary nodes)
- Shansyn: spherical harmonics package for GMT/netcdf grd files
- SHAPE: Spherical HArmonic Parameterization Explorer
Ссылки[править | править код]
- Spherical harmonics applied to Acoustic Field analysis on Trinnov Audio’s research page
- Spherical Harmonics by Stephen Wolfram and Nodal Domains of Spherical Harmonics by Michael Trott, The Wolfram Demonstrations Project
- An accessible introduction to spherical harmonics (by J. B. Calvert)
- Spherical harmonics entry at Citizendium















![{\displaystyle {\begin{aligned}Y_{\ell m}&={\begin{cases}\displaystyle {i \over {\sqrt {2}}}\left(Y_{\ell }^{m}-(-1)^{m}\,Y_{\ell }^{-m}\right)&{\text{ }}\ m<0\\\displaystyle Y_{\ell }^{0}&{\text{ }}\ m=0\\\displaystyle {1 \over {\sqrt {2}}}\left(Y_{\ell }^{-m}+(-1)^{m}\,Y_{\ell }^{m}\right)&{\text{ }}\ m>0.\end{cases}}\\&={\begin{cases}\displaystyle {\sqrt {2}}\,(-1)^{m}\,\operatorname {Im} [{Y_{\ell }^{|m|}}]&{\text{ }}\ m<0\\\displaystyle Y_{\ell }^{0}&{\text{ }}\ m=0\\\displaystyle {\sqrt {2}}\,(-1)^{m}\,\operatorname {Re} [{Y_{\ell }^{m}}]&{\text{ }}\ m>0.\end{cases}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35f77a55bfe53007193bf360c5fb1f53c55011f9)










![{\displaystyle {\hat {D}}(\alpha ,\beta ,\gamma )Y_{l}^{m}(\theta ,\varphi )=Y_{\ell }^{m}(\theta ',\varphi ')=\sum _{m'=-\ell }^{\ell }[D_{mm'}^{(\ell )}(\alpha ,\beta ,\gamma )]^{*}Y_{\ell }^{m'}(\theta ,\varphi ),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b4af9fcca20b758b54bfd7755fd70c1232a8854)



