Теорема Ньютона — Лейбница
Формула Ньютона — Лейбница, или основная теорема анализа, даёт соотношение между двумя операциями: взятием интеграла Римана и вычислением первообразной.
Формулировка[править | править код]
Классическая формулировка формулы Ньютона-Лейбница имеет следующий вид.
|
Если функция непрерывна на отрезке и — любая её первообразная на этом отрезке, то имеет место равенство |
Пусть на отрезке задана интегрируемая функция .
Зададим произвольное значение и определим новую функцию . Она определена для всех значений , потому что мы знаем, что если существует интеграл от на , то существует также интеграл от на , где . Напомним, что мы считаем по определению
(1)
Заметим, что
Покажем, что непрерывна на отрезке . В самом деле, пусть ; тогда
и если , то
Таким образом, непрерывна на независимо от того, имеет или не имеет разрывы; важно, что интегрируема на .
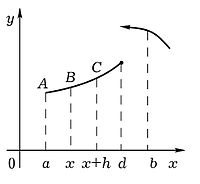
Пусть теперь функция не только интегрируема на , но непрерывна в точке . Докажем, что тогда имеет в этой точке производную, равную
(2)
В самом деле, для указанной точки
(1) , (3)
Мы положили , а так как постоянная относительно , то . Далее, в силу непрерывности в точке для всякого можно указать такое , что для .
Поэтому
что доказывает, что левая часть этого неравенства есть о(1) при .
Переход к пределу в (3) при показывает существование производной от в точке и справедливость равенства (2). При речь здесь идёт соответственно о правой и левой производной.
Если функция непрерывна на , то на основании доказанного выше соответствующая ей функция
(4)
имеет производную, равную . Следовательно, функция есть первообразная для на .
Это заключение иногда называется теоремой об интеграле с переменным верхним пределом, или теоремой Барроу.
Мы доказали, что произвольная непрерывная на отрезке функция имеет на этом отрезке первообразную, определенную равенством (4). Этим доказано существование первообразной для всякой непрерывной на отрезке функции.
Пусть теперь есть произвольная первообразная функции на . Мы знаем, что , где — некоторая постоянная. Полагая в этом равенстве и учитывая, что , получим .
Таким образом, . Но
Поэтому
Однако на самом деле требование непрерывности подынтегральной функции избыточно. Для выполнения этой формулы достаточно лишь существование левой и правой частей.
|
Если функция интегрируема и имеет первообразную на отрезке , — любая её первообразная на этом отрезке, то имеет место равенство |
Непрерывность является удобным условием на практике, поскольку сразу же гарантирует и интегрируемость, и существование первообразной. В случае её отсутствия же для правильного применения требуется проверка обоих этих свойств, что иногда бывает сложным. Существуют интегрируемые функции, не имеющие первообразной (любая функция с конечным числом точек разрыва или функция Римана), и неинтегрируемые, имеющие первообразную (производная , дополненная нулём в нуле, на любом отрезке, содержащем 0, или функция Вольтерры).
Формула может быть обобщена для случая функций с конечным числом разрывов. Для этого нужно обобщить понятие первообразной. Пусть функция определена на отрезке за исключением, возможно, конечного числа точек. Функция называется обобщённой первообразной , если она:
- Непрерывна на отрезке
- Во всех точках , за исключением, возможно, конечного их числа, дифференцируема
- Во всех точках, где она дифференцируема, за исключением, возможно, конечного их числа, её производная равна .
Это определение не требует, чтобы производная равнялась во всех точках, где дифференцируема. С этим понятием можно обобщить формулу Ньютона — Лейбница ещё сильнее.
|
Пусть определена на везде, за исключением, возможно, конечного числа точек. Если функция интегрируема и имеет обобщённую первообразную на отрезке , — любая её обобщённая первообразная на этом отрезке, то имеет место равенство |
Так как функция интегрируема, можно рассмотреть любую последовательность разбиений с отмеченными точками, диаметр которых стремится к нулю. Предел интегральных сумм по ним будет равен интегралу.
Рассмотрим последовательность разбиений отрезка такую, что диаметр разбиения при стремится к нулю. Включим в каждое из этих разбиений также точки отрезка , в которых не дифференцируема или её производная не равна . С этими дополнительными точками разбиения обозначим .
Теперь зададим на них отмеченные точки. Фиксируем конкретное разбиение . Тогда, по условию, функция непрерывна на каждом из отрезков и дифференцируема на интервалах . Условия теоремы Лагранжа соблюдены и, значит, существует такая точка , что . Эти точки возьмём в качестве отмеченных точек разбиения . Тогда интегральная сумма по такому разбиению будет равна Интегральная сумма каждого из размеченных разбиений (T_n',Xi_n) равна одному и тому же значению, следовательно, и предел этих сумм будет равен этому значению, то есть
- .
Приведённое доказательство интересно тем, что в нём не использовалась ни одно из свойств интеграла, кроме непосредственно его определения. Однако доказательство формулы Ньютона-Лейбница в классической формулировке оно не даёт: для этого необходимо дополнительно доказать, что любая непрерывная функция интегрируема и имеет первообразную.
Замечание. Бездумное применение формулы к функциям, не являющимся непрерывными, может привести к ошибке. Пример неправильного вычисления:
- хотя интеграл от положительной функции не может быть отрицателен.
Причина ошибки: функции не является первообразной (даже обобщённой) для функции на отрезке просто потому, что она не определена в нуле. Функция не имеет на этом отрезке первообразной вообще. Более того, эта функция ещё и не ограничена в окрестности нуля, и следовательно, не интегрируема по Риману.
История[править | править код]
Ещё до появления математического анализа данная теорема (в геометрической или механической формулировке) была известна Грегори и Барроу. Например, Барроу описал этот факт в 1670 году как зависимость между задачами на квадратуры и на проведение касательных.
Ньютон сформулировал теорему словесно следующим образом: «Для получения должного значения площади, прилегающей к некоторой части абсциссы, эту площадь всегда следует брать равной разности значений z [первообразной], соответствующих частям абсцисс, ограниченным началом и концом площади».
У Лейбница запись данной формулы в современном виде также отсутствует, поскольку обозначение определённого интеграла появилось гораздо позже, у Фурье в начале XIX века.
Современную формулировку привёл Лакруа в начале XIX века.
Значение[править | править код]
Основная теорема анализа устанавливает связь между дифференциальным и интегральным исчислениями. Понятие первообразной (а значит, и понятие неопределённого интеграла) определяется через понятие производной и, таким образом, относится к дифференциальному исчислению. С другой стороны, понятие определённого интеграла Римана формализуется как предел, к которому сходится так называемая интегральная сумма. Оно независимо от понятия производной и относится к другой ветви анализа — интегральному исчислению. Формула Ньютона — Лейбница же позволяет выразить определённый интеграл через первообразную.
Интеграл Лебега[править | править код]
Функция представляет собой неопределённый интеграл суммируемой функции . Функция является абсолютно непрерывной.
Теорема (Лебега): абсолютно непрерывна на отрезке тогда и только тогда, когда существует суммируемая на функция такая, что при любом значении x от a до b.
Из этой теоремы вытекает, что если функция абсолютно непрерывна на , то её производная существует почти всюду, суммируема и удовлетворяет равенству[1]:
- , где .
Некоторые следствия[править | править код]
В качестве следствий этой теоремы можно назвать формулу замены переменных, а также теорему о разложении монотонных функций по Лебегу[1].
Интегрирование по частям[править | править код]
Пусть и — абсолютно непрерывные функции на отрезке . Тогда:
- .
Формула следует немедленно из основной теоремы анализа и правила Лейбница[1].
Вариации и обобщения[править | править код]
См. также[править | править код]
Примечания[править | править код]
- ↑ 1 2 3 Богачёв В. И., Смолянов О. Г. Действительный и функциональный анализ: университетский курс. — М.-Ижевск: НИЦ "Регулярная и хаотическая динамика", Институт компьютерных исследований, 2009. — С. 188-197. — 724 с. — ISBN 978-5-93972-742-6.
Литература[править | править код]
- Демидович Б. П. Отдел 3. Формула Ньютона — Лейбница // Сборник задач и упражнений по математическому анализу. — 1990. — (Курс высшей математики и математической физики).
- Камынин Л. И. Математический анализ. Т. 1, 2. — 2001.
- Никифоровский В. А. Путь к интегралу. — М.: Наука, 1985.

![{\displaystyle \left[a,b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f30926fb280a9fdf66fd931e14d4363cb824feaa)



![{\displaystyle \textstyle x\in \left[a,b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26167a01437e354daafca04879c926ceb9845d49)

![{\displaystyle \left[a,x\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/853571555b7143e7d7218bf35a1e739c05153b2d)




![{\displaystyle x,x+h\in \left[a,b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd067d069e553f45ed6b4febcda71e76f3724dbf)










![{\displaystyle x\in \left[a,x\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd8b14d135fa2b135ebac11566907fa56d2ae89a)


























![{\displaystyle [a;b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68e776d74130a8890a814c1f4e74372a9110d2f9)







![{\displaystyle [x_{i-1};x_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a1c62e61054537b8a6952bf19f623388c38b138)









![{\displaystyle [-1;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8bc389ca678dffbedd0d41ca0fecb9806c9b7cf)


![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)



![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce)
