Фильтр Баттерворта
Фильтр Баттерво́рта — один из типов электронных фильтров. Фильтры этого класса отличаются от других методом проектирования. Фильтр Баттерворта проектируется так, чтобы его амплитудно-частотная характеристика была максимально гладкой на частотах полосы пропускания.
Подобные фильтры были впервые описаны британским инженером Стефаном Баттервортом[англ.] в статье «О теории фильтрующих усилителей» (англ. On the Theory of Filter Amplifiers), в журнале Wireless Engineer в 1930 году.
Обзор[править | править код]
АЧХ фильтра Баттерворта максимально гладкая на частотах полосы пропускания и снижается практически до нуля на частотах полосы подавления. При отображении частотного отклика фильтра Баттерворта на логарифмической АФЧХ, амплитуда снижается к минус бесконечности на частотах полосы подавления. В случае фильтра первого порядка АЧХ затухает с крутизной −6 децибел на октаву (-20 децибел на декаду) (на самом деле все фильтры первого порядка независимо от типа идентичны и имеют одинаковый частотный отклик). Для фильтра Баттерворта второго порядка АЧХ затухает на −12 дБ на октаву, для фильтра третьего порядка — на −18 дБ и так далее. АЧХ фильтра Баттерворта — монотонно убывающая функция частоты.
Фильтр Баттерворта — единственный из фильтров, сохраняющий форму АЧХ для более высоких порядков (за исключением более крутого спада характеристики на полосе подавления) тогда как многие другие разновидности фильтров (фильтр Бесселя, фильтр Чебышёва, эллиптический фильтр) имеют различные формы АЧХ при различных порядках.
В сравнении с фильтрами Чебышёва I и II типов или эллиптическим фильтром, фильтр Баттерворта имеет более пологий спад характеристики и поэтому должен иметь больший порядок (что более трудно в реализации) для того, чтобы обеспечить нужные характеристики на частотах полосы подавления. Однако фильтр Баттерворта имеет более линейную фазо-частотную характеристику на частотах полосы пропускания.

Как и для всех фильтров при рассмотрении частотных характеристик используют фильтр нижних частот, из которого легко можно получить фильтр высоких частот, полосовой или режекторный фильтр.
Амплитудно-частотная характеристика фильтра Баттерворта -го порядка может быть получена из передаточной функции :
где
- — порядок фильтра
- — частота среза (частота на которой амплитуда равна −3 дБ)
- — коэффициент усиления по постоянной составляющей (усиление на нулевой частоте)
Легко заметить, что для бесконечных значений АЧХ становится прямоугольной функцией, и частоты ниже частоты среза будут пропускаться с коэффициентом усиления , а частоты выше частоты среза будут полностью подавляться. Для конечных значений спад характеристики будет пологим.
С помощью формальной замены представим выражение в виде :
Полюсы передаточной функции расположены на круге радиуса равноудалённо друг от друга в левой полуплоскости. То есть передаточную функцию фильтра Баттерворта можно определить лишь определением полюсов его передаточной функции в левой полуплоскости s-плоскости. -й полюс определяется из следующего выражения:
откуда
Передаточную функцию можно записать в виде:
Аналогичные рассуждения применимы и к цифровым фильтрам Баттерворта, с той лишь разницей, что соотношения записываются не для s-плоскости, а для z-плоскости.
Знаменатель этой передаточной функции называется полиномом Баттерворта.
Нормированные полиномы Баттерворта[править | править код]
Полиномы Баттерворта могут записываться в комплексной форме, как показано выше, однако обычно они записываются в виде соотношений с вещественными коэффициентами (комплексно-сопряжённые пары объединяются с помощью умножения). Нормируются полиномы по частоте среза: . Нормированные полиномы Баттерворта, таким образом, имеют следующую каноническую форму:
- , — чётно
- , — нечётно
Ниже представлены коэффициенты полиномов Баттерворта для первых восьми порядков:
| Коэффициенты полиномов | |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 |
Максимальная гладкость[править | править код]
Приняв и , производная амплитудной характеристики по частоте будет выглядеть следующим образом:
Она монотонно убывает для всех так как коэффициент усиления всегда положителен. Таким образом, АЧХ фильтра Баттерворта не имеет пульсаций. При разложении амплитудной характеристики в ряд, получим:
Другими словами, все производные амплитудно-частотной характеристики по частоте до -й равны нулю, из чего следует «максимальная гладкость».
Спад характеристики на высоких частотах[править | править код]
Приняв , найдём наклон логарифма АЧХ на высоких частотах:
В децибелах высокочастотная асимптота имеет наклон дБ/декаду.
Проектирование фильтра[править | править код]
Существует ряд различных топологий фильтра, с помощью которых реализуются линейные аналоговые фильтры. Эти схемы отличаются только значениями элементов, структура же остаётся неизменной.
Топология Кауэра[править | править код]
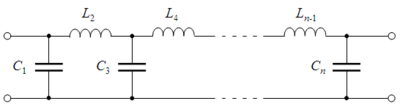
Топология Кауэра использует пассивные элементы (ёмкости и индуктивности)[1]. Фильтр Баттеворта с заданной передаточной функцией может быть построен в форме Кауэра 1 типа. -й элемент фильтра задаётся соотношением:
- ; k нечётно
- ; k чётно
Топология Саллена — Ки[править | править код]
Топология Саллена-Ки использует помимо пассивных также и активные элементы (операционные усилители). Каждый каскад схемы Саллена-Ки представляет собой часть фильтра, математически описываемую парой комплексно-сопряжённых полюсов. Весь фильтр получается последовательным соединением всех каскадов. В случае, если попадается действительный полюс, он должен быть реализован отдельно, обычно в виде RC-цепочки, и включён в общую схему.
Передаточная функция каждого каскада в схеме Саллена-Ки имеет вид:
Нужно, чтобы знаменатель представлял собой один из множителей полинома Баттерворта. Приняв , получим:
и
Последнее соотношение даёт две неизвестных, которые могут быть выбраны произвольно.
Сравнение с другими линейными фильтрами[править | править код]

Рисунок показывает АЧХ фильтра Баттерворта в сравнении с другими популярными линейными фильтрами пятого порядка.
Из рисунка видно, что спад АЧХ фильтра Баттерворта самый медленный из четырёх, однако он имеет и самую гладкую АЧХ на частотах полосы пропускания.
Пример[править | править код]

Рассмотрим аналоговый низкочастотный фильтр Баттерворта третьего порядка с фарад, ом, и генри. Обозначив полное сопротивление ёмкостей как и полное сопротивление индуктивностей как , где — комплексная переменная, и используя уравнения для расчёта электрических схем, получим следующую передаточную функцию для такого фильтра:
АЧХ задаётся уравнением:
а ФЧХ задаётся уравнением:
Групповая задержка определяется как минус производная фазы по круговой частоте и является мерой искажений сигнала по фазе на различных частотах. Логарифмическая АЧХ такого фильтра не имеет пульсаций ни в полосе пропускания, ни в полосе подавления.
График модуля передаточной функции на комплексной плоскости ясно указывает на три полюса в левой полуплоскости. Передаточная функция полностью определяется расположением этих полюсов на единичном круге симметрично относительно действительной оси.
Заменив каждую индуктивность ёмкостью, а ёмкости — индуктивностями, получим высокочастотный фильтр Баттерворта.

См. также[править | править код]
Примечания[править | править код]
- ↑ http://www.falstad.com/circuit/ Архивная копия от 21 января 2013 на Wayback Machine Circuit. Passive Filters. Butterworth Low-Pass (10 pole)
Литература[править | править код]
- В.А. Лукас. Теория автоматического управления. — M.: Недра, 1990.
- Б.Х. Кривицкий. Справочник по теоретическим основам радиоэлектроники. — М.: Энергия, 1977.
- Miroslav D. Lutovac. Filter Design for Signal Processing using MATLAB© and Mathematica©. — New Jersey, USA.: Prentice Hall, 2001. — ISBN 0-201-36130-2.
- Richard W. Daniels. Approximation Methods for Electronic Filter Design. — New York: McGraw-Hill, 1974. — ISBN 0-07-015308-6.
- Steven W. Smith. The Scientist and Engineer’s Guide to Digital Signal Processing. — Second Edition. — San-Diego: California Technical Publishing, 1999. — ISBN 0-9660176-4-1.
- Britton C. Rorabaugh. Approximation Methods for Electronic Filter Design. — New York: McGraw-Hill, 1999. — ISBN 0-07-054004-7.
- B. Widrow, S.D. Stearns. Adaptive Signal Processing. — Paramus, NJ: Prentice-Hall, 1985. — ISBN 0-13-004029-0.
- S. Haykin. Adaptive Filter Theory. — 4rd Edition. — Paramus, NJ: Prentice-Hall, 2001. — ISBN 0-13-090126-1.
- Michael L. Honig, David G. Messerschmitt. Adaptive Filters — Structures, Algorithms, and Applications. — Hingham, MA: Kluwer Academic Publishers, 1984. — ISBN 0-89838-163-0.
- J.D. Markel, A.H. Gray, Jr. Linear Prediction of Speech. — New York: Springer-Verlag, 1982. — ISBN 0-387-07563-1.
- L.R. Rabiner, R.W. Schafer. Digital Processing of Speech Signals. — Paramus, NJ: Prentice-Hall, 1978. — ISBN 0-13-213603-1.
- Richard J. Higgins. Digital Signal Processing in VLSI. — Paramus, NJ: Prentice-Hall, 1990. — ISBN 0-13-212887-X.
- A. V. Oppenheim, R. W. Schafer. Digital Signal Processing. — Paramus, NJ: Prentice-Hall, 1975. — ISBN 0-13-214635-5.
- L. R. Rabiner, B. Gold. Theory and Application of Digital Signal Processing. — Paramus, NJ: Prentice-Hall, 1986. — ISBN 0-13-914101-4.
- John G. Proakis, Dimitris G. Manolakis. Introduction to Digital Signal Processing. — Paramus, NJ: Prentice-Hall, 1988. — ISBN 0-02-396815-X.
Ссылки[править | править код]
- Расчет фильтра Баттерворта с примерами
- The Scientist and Engineer’s Guide to Digital Signal Processing (англ.)
- Фильтры нижних частот
- Использование фильтра Баттерворта в синтезе систем управления Архивная копия от 22 июня 2006 на Wayback Machine
- Расчёт рекурсивных фильтров
- Классификация фильтров
- Circuits. Passiv Filters. Butterworth Low-Pass (10 pole)
















![{\displaystyle B_{n}(s)=\prod _{k=1}^{\frac {n}{2}}\left[s^{2}-2s\cos \left({\frac {2k+n-1}{2n}}\,\pi \right)+1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/187e9a2c6bc7c89f6130001674b6b6b352ed096f)
![{\displaystyle B_{n}(s)=(s+1)\prod _{k=1}^{\frac {n-1}{2}}\left[s^{2}-2s\cos \left({\frac {2k+n-1}{2n}}\,\pi \right)+1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8353ee9b21666bab79a2a0e72a76c5c097a832aa)
















![{\displaystyle C_{k}=2\sin \left[{\frac {(2k-1)}{2n}}\pi \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68f23aa51ad46a68f0cb9d82e2ed3235ef9ee49b)
![{\displaystyle L_{k}=2\sin \left[{\frac {(2k-1)}{2n}}\pi \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b083cc1dc88cd5443bc52baf7f229d1123322de7)
















![{\displaystyle \Phi (\omega )=\arg[H(j\omega )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5415d3b74765eb036dc4c99e9e3e75ad01795e8f)
