Граф без клешней

Материал из Википедии — свободной энциклопедии
Перейти к навигации Перейти к поиску

В теории графов графом без клешней называется граф, который не содержит порождённых подграфов, изоморфных K1,3 (клешней).

Клешнёй называется полный двудольный граф K1,3 (то есть звезда с тремя рёбрами, тремя листьями и одной центральной вершиной). Граф без клешней — это граф, в котором никакой порождённый подграф не является клешнёй, то есть не существует четвёрки вершин A, B, C и O таких, что O соединяется с A, B и C, но вершины A, B и C не соединены между собой. Также можно определить граф без клешней как граф, в котором окрестность любой вершины образует дополнение графа без треугольников.

Другое представление клешни

Графы без клешней первоначально изучались как обобщение рёберных графов и получили дополнительные стимулы, когда были открыты три ключевых факта о них:

  1. факт, что все связные графы без клешней чётного порядка имеют совершенные паросочетания;
  2. открытие полиномиального по времени алгоритма поиска максимального независимого множества в графах без клешней;
  3. описание совершенных графов без клешней[1]. Графам без клешней посвящены сотни статей и несколько обзоров[2].

Примеры[править | править код]

Правильный икосаэдр, многогранник, вершины и рёбра которого формируют граф без клешней.
  • Рёберный граф L(G) любого графа G не имеет клешней. L(G) содержит вершину для каждой дуги G и вершины сопряжены в L(G) когда соответствующие рёбра имеют общую вершину в G. Рёберный граф L(G) не может иметь клешней, поскольку если каждое из трёх рёбер e1, e2, и e3 в G имеет общую вершину с четвёртым ребром e4, то по принципу Дирихле по меньшей мере 2 ребра из e1, e2, и e3 имеют общую вершину. Рёберные графы могут быть описаны девятью запрещёнными подграфами[3] и клешня является простейшим из этих девяти графов. Это даёт мотив для изучения графов без клешней[1].

Распознавание[править | править код]

Можно проверить напрямую, что заданный граф с n вершинами и m рёбрами не имеет клешней за время O(n4) путём проверки каждой четвёрки вершин — не порождают ли они клешню[6]. Несколько эффективнее, но сложнее, можно проверить, что граф не имеет клешней путём проверки для каждой вершины графа, что дополнение графа соседей вершины не содержит треугольника. Граф содержит треугольник в том и только в том случае, если куб матрицы смежности содержит ненулевой диагональный элемент, так что поиск треугольника может быть осуществлён за то же асимптотическое время, что и умножение матриц n × n [7]. Таким образом, при использовании алгоритма Копперсмита — Винограда, общее время определения, есть ли у графа клешни, будет O(n3.376).

Клокс, Крач и Мюллер (Kloks, Kratsch, Müller)[8] обратили внимание на то, что в графе без клешней каждая вершина имеет максимум соседей, в противном случае по теореме Турана окрестность вершины не будет иметь достаточное число рёбер, чтобы сформировать дополнение графу без треугольников. Это наблюдение позволяет проверить соседей c использованием упомянутого ранее алгоритма быстрого произведения матриц за то же асимптотическое время . Худший случай этого алгоритма возникает, когда Ω(√m) вершин имеют по Ω(√m) соседей каждая, а остальные вершины имеют мало соседей, в этом случае общее время равно (m3.376/2) = O(m1.688).

Перечисление[править | править код]

Поскольку графы без клешней включают все дополнения графам без треугольников, число графов без клешней с n вершинами растёт как минимум с той же скоростью, что и число графов без треугольников, то есть по экспоненте от корня из n. Число связных графов без клешней с n рёбрам, для n = 1, 2, …

1, 1, 2, 5, 14, 50, 191, 881, 4494, 26389, 184749, … последовательность A022562 в OEIS.

Если графы могут быть несвязны, число графов больше:

1, 2, 4, 10, 26, 85, 302, 1285, 6170, … последовательность A086991 в OEIS.

Техника Палмера, Рида и Робинсона (Palmer, Read, Robinson, 2002)[9] позволяет посчитать число кубических графов без клешней очень эффективно, что необычно для задач перечисления графов.

Паросочетания[править | править код]

Доказательство Самнера, что связные графы без клешней чётного порядка имеют совершенное паросочетание: удаление двух смежных вершин v и w, наиболее удалённых от u, оставляет подграф связным, что позволяет продолжить процесс.

Самнер (Sumner, 1974)[10] и, независимо, Лас Вергнас (Las Vergnas, 1975)[11] доказали, что любой связный граф без клешней с чётным числом вершин имеет совершенное паросочетание[12]. То есть существует множество рёбер в графе, такое, что каждая вершина является конечной вершиной в точности одного ребра из паросочетания. Из этого следует, что для рёберных графов, имеющих чётное число рёбер, можно разбить все рёбра на пути длиной два. Совершенные паросочетания могут быть использованы для ещё одной характеристики графов без клешней — это в точности те графы, в которых любой связный порождённый подграф чётного порядка имеет совершенное паросочетание[12].

Доказательство Самнера показывает, строго говоря, что в любом связном графе без клешней можно найти пару сопряжённых вершин, удаление которых оставляет граф связным. Для доказательства этого Самнер находит пару вершин u и v, которые насколько можно далеки друг от друга, и выбирает w среди соседей вершины v, удалённую от u насколько возможно. Как он показал, ни v, ни w не могут лежать на кратчайшем пути от любой другой вершины до u, так что удаление вершин v и w оставляет граф связным. Последовательное удаление таких пар образует совершенное паросочетание в графе без клешней.

Та же самая идея доказательства работает и в более общем случае: если u — любая вершина, v — любая вершина, максимально удалённая от u, и w — любая соседняя вершина v, максимально удалённая от u. Теперь удаление v и w из графа не меняет расстояний до u. Таким образом, процесс формирования паросочетаний путём нахождения и удаления пар vw, максимально удалённых от u, может быть совершён за линейное время простым обходом дерева поиска в ширину, начатого с вершины u. Хробак, Наор и Новик (Chrobak, Naor, Novick, 1989)[13] дали другой линейный по времени алгоритм, основанный на поиске в глубину, а также эффективные параллельные алгоритмы для той же задачи.

Фаудри, Фландрин и Риячек (Faudree, Flandrin, Ryjáček)[2] дали несколько близких результатов, включая следующие:

  1. (r − 1)-связный граф, не содержащий K1,r подграфов нечётного порядка имеют совершенные паросочетания для любого r ≥ 2.
  2. Графы нечётного порядка без клешней с максимум одной вершиной степени один могут быть разделены на один нечётный цикл и паросочетание.
  3. Для любого k, не меньшего половины минимальной степени графа без клешней, в котором либо k, либо число вершин чётно, граф имеет k-фактор.
  4. Если граф без клешней является (2k + 1)-связным, то любое k-рёберное паросочетание может быть расширено до совершенного паросочетания.

Независимые множества[править | править код]

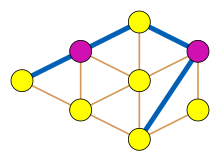
Немаксимальное независимое множество (два фиолетовых ребра) и пополняющий путь

Независимое множество в рёберном графе соответствует паросочетанию в исходном графе, то есть набору рёбер, в котором никакие два ребра не имеют общих точек. Как показал Эдмондс (Edmonds, 1965)[14], максимальное паросочетание в любом графе может быть найдено за полиномиальное время; Сбихи (Sbihi, 1980)[15] расширил этот алгоритм, так что новый алгоритм находит максимальное независимое множество в любом графе без клешней[16]. Минти (Minty, 1980)[17] (исправлен Накамурой и Тамурой (Nakamura, Tamura, 2001) [18]) дал другое расширение алгоритмов Эдмонда для графов без клешней, преобразующего задачу в поиск паросочетания во вспомогательном графе, получаемом из исходного графа без клешней. Подход Минти может быть использован для решения за полиномиальное время более общей задачи нахождения независимого множества максимального веса. Существует обобщение этих результатов на широкий класс графов[16].

Как заметил Сбихи, если  — независимое множество в графе без клешней, то любая вершина графа может иметь максимум две соседние вершины из  — три соседние вершины образовали бы клешню. Сбихи называет вершину насыщенной, если она имеет две соседние из и ненасыщеной, если она не принадлежит и в то же время имеет меньше двух соседей из . Из наблюдения Сбихи следует, что если и есть независимые множества, граф, порождённый , должен иметь степень не выше второй. Таким образом, он является объединением путей и циклов. В частности, если  — не максимальное независимое множество, оно отличается от любого максимального независимого множества циклами и пополняющими путями, то есть путями, в которых вершины из и не из чередуются, и у которых обе конечные вершины не насыщены. Симметрическая разность графов и пополняющего пути есть максимальное независимое множество (Симметрическая разность графов H и G, имеющих один и тот же набор вершин V — это граф с тем же набором вершин V, содержащий рёбра G и H, но не содержащий общих рёбер, принадлежащих как G, так и H). Алгоритм Сбихи последовательно увеличивает размер независимого множества путём нахождения пополняющих путей, пока такие пути можно найти.

Нахождение пополняющего пути является сложной задачей, поскольку расширение пути может и не существовать, если он содержит ребро между двумя вершинами, не принадлежащими . К счастью, это может случиться только в двух случаях: две смежные вершины могут быть конечными вершинами пути или между ними лежит одна вершина, смежная обоим. Любая другая смежная вершина приведёт к клешне. От смежных конечных вершин можно избавиться, временно удаляя все смежные v-вершины перед поиском пополняющего пути, начинающего в v. Если путь найден не будет, вершину v можно удалить из графа до конца алгоритма. После такой редукции графа задача может быть описана в терминах графа-переключателя[en], хотя Сбихи и не пользовался этой терминологией. Граф-переключатель — это ненаправленный граф, в котором дуги любой вершины разделены на две группы, и любой путь, проходящий через вершину, обязан содержать рёбра из обеих групп. Можно построить граф-переключатель на множестве насыщенных и ненасыщенных вершин графа без клешней, рёбра которого соединяют вершины, если они не являются смежными в исходном графе, и существует путь длины 2 между ними, проходящий через вершину из I. Два множества рёбер в каждой вершине образуются двумя вершинами I, через которые эти пути длины 2 проходят. Путь в графе-переключателе между двумя ненасыщенными вершинами соответствует пополняющему пути в исходном графе. Граф-переключатель имеет квадратичную сложность и путь в нём может быть найден за линейное время, а за всё время работы алгоритма может потребоваться найти O(n) пополняющих путей. Таким образом, алгоритм Сбихи требует O(n3) времени работы.

Раскраска, клики и доминирование[править | править код]

Совершенный граф — это граф, в котором хроматическое число и размер максимальной клики[en] равны, и в котором это равенство существует в любом индуцированном подграфе. Известно (по строгой теореме о совершенных графах), что совершенные графы могут быть охарактеризованы как графы, не имеющие в качестве индуцированных подграфов нечётные циклы или дополнения нечётным циклам (так называемые нечётные дыры)[5]. Однако многие годы этот факт оставался гипотезой, доказанной только для специальных подклассов графов. Одним из таких подклассов было семейство графов без клешней — несколько авторов обнаружили, что графы без клешней и без нечётных циклов и дыр совершенны. Совершенность графа без клешней может быть проверена за полиномиальное время. В совершенном графе без клешней окрестность любой вершины образует дополнение двудольного графу. Можно раскрасить совершенный граф без клешней или в нём найти максимальную клику за полиномиальное время[19].

Если граф без клешней не совершенен, задача поиска максимальной клики становится NP-трудной[6]. Задача нахождения оптимальной раскраски такого графа тоже NP-трудна, поскольку (через рёберный граф) эта задача обобщает NP-трудную задачу вычисления хроматического числа графа[6]. По той же причине NP-трудной задачей является поиск алгоритма раскраски, гарантированная эффективность которого лучше, чем 4/3. Однако гарантированную эффективность, равную двум, можно получить в алгоритме жадной раскраски, поскольку хроматическое число графа без клешней больше, чем половина его максимальной степени.

Хотя не все графы без клешней совершенны, графы без клешней удовлетворяют другому свойству, связанному с совершенством. Граф называется совершенным графом доминирования[en], если он имеет минимальное доминирующее множество, являющееся независимым множеством вершин, и если тем же самым свойством обладают все порождённые подграфы. Графы без клешей обладают этим свойством. Чтобы показать это, допустим, что D — доминирующее множество в графе без клешней и пусть v и w — две сопряжённые вершины D. Тогда множество вершин, доминируемых вершиной v, но не w, должно быть кликой (в противном случае v окажется центром клешни). Если каждая вершина этой клики уже доминируется, по крайней мере, одним членом множества D, то v может быть удалена с порождением меньшего независимого доминирующего множества. В противном же случае v можно заменить одной из недоминируемых вершин из клики, порождая доминирующее множество с меньшим числом смежных вершин. Повторяя эти замены, мы достигнем доминирующего множества, не превосходящего D, так что, если начальное D — минимальное доминирующее множество, процесс закончится созданием равного по размеру независимого доминирующего множества[20].

Несмотря на свойство совершенного доминирования, определение размера минимального доминирующего множества в графе без клешней является NP-трудной задачей[6]. Однако в контраст с более общими классами графов, поиск минимального доминирующего множества в графе без клешней обладает параметрической сложностью с фиксированными параметрами[en] — задача может быть решена за время, полиномиально зависящее от размера графа и экспоненциально от размера доминирующего множества[21] [22].

Структура[править | править код]

В серии статей Чудновская и Сеймур[23] доказали структурную теорию графов без клешней, аналогичную теореме о структуре графов для семейств минорно-замкнутых графов, доказанную Робертсоном (Robertson) и Сеймуром (Seymour), и структурной теории для совершенных графов, которую Чудновская (Chudnovsky), Сеймур (Seymour) и их соавторы использовали для доказательства теоремы о строго совершенном графе[5]. Теория слишком сложна, чтобы описывать её детально здесь, но чтобы показать её красоту, опишем пару их результатов. Во-первых, для специального подкласса графов без клешней, который они назвали квазирёберные графы (или локально квазидвудольные графы), они утверждают, что каждый такой граф имеет одну из двух форм:

  1. Нечёткий круговой интервальный граф — класс графов, которые геометрически можно представить как точки и дуги на окружности.
  2. Граф, который можно построить из мультиграфа путём замены каждого ребра нечётким линейным интервальным графом. Это обобщает конструкцию рёберных графов, в которых каждое ребро мультиграфа заменяется вершиной. Нечёткие линейные интервальные графы строятся так же, как и нечёткие круговые интервальные графы, только на отрезке, а не на окружности.

Чудновская и Сеймур классифицировали произвольные связные графы без клешней следующим образом:

  1. Шесть специфичных графов без клешней. Три из них являются рёберными графами, некоторые графы дуг окружности и порождённые подграфы икосаэдра. Оставшиеся три требуют дополнительных определений.
  2. Графы, образованные четырьмя простыми способами из меньших графов без клешней.
  3. Антипризматические графы — класс плотных графов, определяются как графы без клешней, в которых любые четыре вершины порождают подграф с минимум двумя рёбрами.

Большая часть их работы по классификации посвящена анализу антипризматических графов. Граф Шлефли, сильно регулярный граф без клешней с параметрами srg(27,16,10,8), играет важную роль в этой части анализа. Эта структурная теория привела к новому продвижению в комбинаторике многранников и новым границам хроматических чисел графов без клешней[5], а также к новым алгоритмам параметрической сложности с фиксированными параметрами для доминирующих множеств в графах без клешней[22].

Примечания[править | править код]

  1. ↑ 1 2 Faudree, Flandrin, Ryjáček, 1997, p. 88.
  2. ↑ 1 2 Faudree, Flandrin, Ryjáček, 1997.
  3. ↑ L. W. Beineke. Beiträge zur Graphentheorie. — Teubner, 1968. — С. 17—33.
  4. ↑ 1 2 Faudree, Flandrin, Ryjáček, 1997, p. 89.
  5. ↑ 1 2 3 4 5 Maria Chudnovsky, Neil Robertson, Paul Seymour, Robin Thomas. The strong perfect graph theorem. — 2006. — Т. 164, вып. 1. — С. 51—229. — doi:10.4007/annals.2006.164.51.
  6. ↑ 1 2 3 4 Faudree, Flandrin, Ryjáček, 1997, p. 132.
  7. ↑ Alon Itai, Michael Rodeh. Finding a minimum circuit in a graph // SIAM Journal on Computing. — 1978. — Т. 7, вып. 4. — С. 413—423. — doi:10.1137/0207033.
  8. ↑ Ton Kloks, Dieter Kratsch, Haiko Müller. Finding and counting small induced subgraphs efficiently // Information Processing Letters. — 2000. — Т. 74, вып. 3—4. — С. 115—121. — doi:10.1016/S0020-0190(00)00047-8.
  9. ↑ Edgar M. Palmer, Ronald C. Read, Robert W. Robinson. Counting claw-free cubic graphs // SIAM Journal on Discrete Mathematics. — 2002. — Т. 16, вып. 1. — С. 65—73. — doi:10.1137/S0895480194274777.
  10. ↑ David P. Sumner. Graphs with 1-factors. — 1974. — Т. 42, вып. 1. — С. 8—12. — doi:10.2307/2039666. — JSTOR 2039666.
  11. ↑ M. Las Vergnas. A note on matchings in graphs // Cahiers du Centre d'Études de Recherche Opérationnelle. — 1975. — Т. 17, вып. 2—3—4. — С. 257—260.
  12. ↑ 1 2 Faudree, Flandrin, Ryjáček, 1997, p. 120—124.
  13. ↑ Marek Chrobak, Joseph Naor, Mark B. Novick. Algorithms and Data Structures[en]: Workshop WADS '89, Ottawa, Canada, August 1989, Proceedings. — Springer, 1989. — Т. 382. — С. 147—162. — doi:10.1007/3-540-51542-9_13.
  14. ↑ Jack Edmonds. Paths, Trees and Flowers // Canadian J. Math. — 1965. — Т. 17, вып. 0. — С. 449—467. — doi:10.4153/CJM-1965-045-4.
  15. ↑ Najiba Sbihi. Algorithme de recherche d'un stable de cardinalité maximum dans un graphe sans étoile // Discrete Mathematics. — 1980. — Т. 29, вып. 1. — С. 53—76. — doi:10.1016/0012-365X(90)90287-R.
  16. ↑ 1 2 Faudree, Flandrin, Ryjáček, 1997, p. 133—134.
  17. ↑ George J. Minty. On maximal independent sets of vertices in claw-free graphs // Journal of Combinatorial Theory. Series B. — 1980. — Т. 28, вып. 3. — С. 284—304. — doi:10.1016/0095-8956(80)90074-X.
  18. ↑ Daishin Nakamura, Akihisa Tamura. A revision of Minty's algorithm for finding a maximum weighted stable set of a claw-free graph // Journal of the Operations Research Society of Japan. — 2001. — Т. 44, вып. 2. — С. 194—204.
  19. ↑ Faudree, Flandrin, Ryjáček, 1997, p. 135—136.
  20. ↑ Faudree, Flandrin, Ryjáček, 1997, p. 124—125.
  21. ↑ Marek Cygan, Geevarghese Philip, Marcin Pilipczuk, Michał Pilipczuk, Jakub Onufry Wojtaszczyk. Dominating set is fixed parameter tractable in claw-free graphs. — 2010.
  22. ↑ 1 2 Danny Hermelin, Matthias Mnich, Erik Jan van Leeuwen, Gerhard Woeginger. Domination when the stars are out. — 2010.
  23. ↑ Maria Chudnovsky, Paul Seymour. Surveys in combinatorics 2005 год. — Cambridge Univ. Press, 2005. — Т. 327. — С. 153—171.

Литература[править | править код]

  • Ralph Faudree, Evelyne Flandrin, Zdeněk Ryjáček. Claw-free graphs — A survey // Discrete Mathematics. — 1997. — Т. 164, вып. 1—3. — С. 87—147. — doi:10.1016/S0012-365X(96)00045-3.

Ссылки[править | править код]

Источник — https://ru.wikipedia.org/w/index.php?title=Граф_без_клешней&oldid=124329948