Куб (алгебра)

y=x³, при целых значениях x на отрезке от 1 до 25

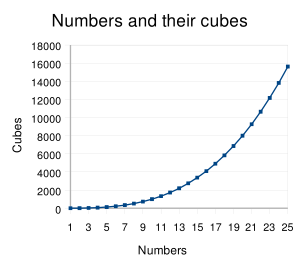
Кубом числа называется результат умножения числа на само себя трижды (возведения числа в степень 3). Куб величины $x$ обозначается так:

$x^3$.

Далее приведено начало числовой последовательности для кубов неотрицательных чисел (последовательность A000578 в OEIS):

0, 1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, 1331, 1728, 2197, 2744, 3375, 4096, 4913, 5832, 6859, 8000, 9261, 10648, 12167, 13824, 15625, 17576, 19683, 21952, 24389, 27000, 29791, 32768, 35937, 39304, 42875, 46656, 50653, 54872, 59319, 64000, 68921, 74088, 79507, 85184, 91125, 97736, 103823, 110592, 117649, 125000, 132651, 140608, 148877, 157464, 166375, 175616, 185193, 195112, 205379, 216000, 226981, 238328…

Сумма кубов первых $n$ положительных чисел вычисляется по формуле: $\sum_{i=1}^n i^3 = 1^3 + 2^3 + 3^3 + ... + n^3 = \left(\frac {n(n+1)}{2}\right)^2$

Геометрический смысл

Куб числа равен объёму куба с длиной ребра, равной этому числу.

Некоторые свойства

• В десятичной записи куб может кончаться на любую цифру (в отличие от квадрата)
• В десятичной записи две последние цифры куба могут быть 00, 01, 03, 04, 07, 08, 09, 11, 12, 13, 16, 17, 19, 21, 23, 24, 25, 27, 28, 29, 31, 32, 33, 36, 37, 39, 41, 43, 44, 47, 48, 49, 51, 52, 53, 56, 57, 59, 61, 63, 64, 67, 68, 69, 71, 72, 73, 75, 76, 77, 79, 81, 83, 84, 87, 88, 89, 91, 92, 93, 96, 97, 99. Зависимость предпоследней цифры куба от последней можно представить в виде следующей таблицы:

последняя цифра	предпоследняя цифра
0	0
5	2, 7
4, 8	чётная
2, 6	нечётная
1, 3, 7, 9	любая

См. также

• Кубический корень — обратная операция по отношению к возведению в куб.
• Квадрат