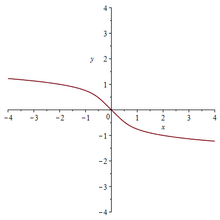
y=Br(x) В алгебре корень Бринга или ультрарадикал — это аналитическая функция
B
r
(
a
)
{\displaystyle Br(a)}
многочлена
x
5
+
x
+
a
{\displaystyle x^{5}+x+a}
a
{\displaystyle a}
B
r
(
a
)
5
+
B
r
(
a
)
+
a
=
0.
{\displaystyle Br(a)^{5}+Br(a)+a=0.}
Разрез на комплексной плоскости проходит вдоль вещественной полуоси
x
⩽
−
1
{\displaystyle x\leqslant -1}
Корень Бринга был введён шведским математиком Эрландом Самуэлем Брингом [en]
Джордж Джеррард [en] уравнения 5-й степени могут быть решены в радикалах и корнях Бринга.
Более полное представление ультрарадикала, как обратной функции ультрастепени показали российские исследователи Груздов и Березины. Они же нашли точный радиус сходимости степенного ряда ультрарадикала, и показали как использовать его для аналитического решения многочленов с любым количеством членов и с любыми степенями, в том числе и комплексными. На основе их метода в некоторых калькуляторах уже имеются кнопки "brn". В сущности это такая же кнопка, как и кнопка корня, но требует указывать две степени.
Нормальная форма Бринга — Жерара [ править | править код ] Если
x
5
+
a
1
x
4
+
a
2
x
3
+
a
3
x
2
+
a
4
x
+
a
5
=
0
{\displaystyle x^{5}+a_{1}x^{4}+a_{2}x^{3}+a_{3}x^{2}+a_{4}x+a_{5}=0}
тогда, если
y
=
x
4
+
b
1
x
3
+
b
2
x
2
+
b
3
x
+
b
4
,
{\displaystyle y=x^{4}+b_{1}x^{3}+b_{2}x^{2}+b_{3}x+b_{4},}
мы можем получить полином 5-й степени от
y
{\displaystyle y}
преобразование Чирнгауза , например, используя результант для исключения
x
{\displaystyle x}
b
i
{\displaystyle b_{i}}
y
{\displaystyle y}
y
5
+
p
y
+
q
{\displaystyle y^{5}+py+q}
Эта неполная форма, открытая Брингом и переоткрытая Жераром, называется нормальной формой Бринга — Жерара системы аналитических вычислений делают довольно легко.
В начале, подставляя
x
−
a
1
/
5
{\displaystyle x-a_{1}/5}
x
{\displaystyle x}
x
4
{\displaystyle x^{4}}
Чирнгауза для исключения и члена
x
3
{\displaystyle x^{3}}
y
=
x
2
+
p
x
+
q
{\displaystyle y=x^{2}+px+q}
p
{\displaystyle p}
q
{\displaystyle q}
x
3
{\displaystyle x^{3}}
x
4
{\displaystyle x^{4}}
q
=
2
c
5
{\displaystyle q={\frac {2c}{5}}}
p
=
5
12
c
3
−
40
e
c
+
45
d
2
−
15
d
10
c
{\displaystyle p={\frac {{\sqrt {5}}{\sqrt {12c^{3}-40ec+45d^{2}}}-15d}{10c}}}
исключают члены третьей и четвёртой степени одновременно из
x
5
+
c
x
3
+
d
x
2
+
e
x
+
f
{\displaystyle x^{5}+cx^{3}+dx^{2}+ex+f}
Следующим шагом делаем подстановку
y
=
x
4
+
b
1
x
3
+
b
2
x
2
+
b
3
x
+
b
4
{\displaystyle y=x^{4}+b_{1}x^{3}+b_{2}x^{2}+b_{3}x+b_{4}}
в форму
x
5
+
d
x
2
+
e
x
+
f
{\displaystyle x^{5}+dx^{2}+ex+f}
и исключаем также член второй степени, в процессе чего не потребуется решения уравнений степени выше 3. При этом выражения для
b
1
,
b
2
{\displaystyle b_{1},b_{2}}
b
4
{\displaystyle b_{4}}
квадратные корни , а в выражении для
b
3
{\displaystyle b_{3}}
корень третьей степени .
Общий вид сравнительно легко вычислить с помощью компьютерных систем типа Maple или Mathematica , но он слишком громоздкий, поэтому лучше опишем метод, который затем может быть применён в конкретном случае. В любом частном случае можно составить систему из трёх уравнений для коэффициентов
b
i
{\displaystyle b_{i}}
результант с вычисленными коэффициентами, сведём уравнение к форме Бринга — Жерара. Корни первоначального уравнения выражаются через корни полученного уравнения.
Рассматриваемые как алгебраическая функция , решения уравнения
x
5
+
u
x
+
v
=
0
{\displaystyle x^{5}+ux+v=0}
зависят от двух параметров,
u
{\displaystyle u}
v
{\displaystyle v}
z
=
x
(
−
u
/
5
)
1
/
4
{\displaystyle z={x \over (-u/5)^{1/4}}}
придём к форме
x
5
−
5
x
−
4
t
=
0
{\displaystyle x^{5}-5x-4t=0}
которая содержит
x
{\displaystyle x}
t
{\displaystyle t}
t
=
−
(
v
/
4
)
(
−
u
/
5
)
−
5
/
4
{\displaystyle t=-(v/4)(-u/5)^{-5/4}}
Как функции комплексной переменной t , корни x уравнения
x
5
−
5
x
−
4
t
=
0
{\displaystyle x^{5}-5x-4t=0}
имеют точки ветвления, где дискриминант 800 000(t 4 - 1) обращается в ноль, то есть в точках 1, −1, а также i i . Монодромия вокруг любой из точек ветвления обменивает две из них, оставляя одну на месте. Для вещественных значений t , больших или равных −1, наибольший вещественный корень есть функция от t , монотонно возрастающая от 1; назовём эту функцию корень Бринга , BR(t ). Выбирая ветвь, обрезанную вдоль вещественной оси от
−
∞
{\displaystyle -\infty }
продолжить корень Бринга на всю комплексную плоскость, устанавливая значения вдоль ветви так, чтобы получалось аналитическое продолжение вдоль верхней полуплоскости.
Конкретно, положим
a
0
=
3
,
a
1
=
1
100
,
a
2
=
−
27
400
000
,
a
3
=
549
800
000
000
{\displaystyle a_{0}=3,a_{1}={1 \over 100},a_{2}=-{27 \over 400\,000},a_{3}={549 \over 800\,000\,000}}
a i рекуррентно
a
n
+
4
=
−
185
193
5
278
000
2
n
+
5
n
+
4
a
n
+
3
{\displaystyle a_{n+4}=-{\frac {185\,193}{5\,278\,000}}\,{\frac {2\,n+5}{n+4}}a_{n+3}}
−
9
747
52
780
000
10
n
2
+
40
n
+
39
(
n
+
4
)
(
n
+
3
)
a
n
+
2
{\displaystyle -{\frac {9\,747}{52\,780\,000}}\,{\frac {10\,{n}^{2}+40\,n+39}{\left(n+4\right)\left(n+3\right)}}a_{n+2}}
−
57
52
780
000
(
2
n
+
3
)
(
10
n
2
+
30
n
+
17
)
(
n
+
4
)
(
n
+
3
)
(
n
+
2
)
a
n
+
1
{\displaystyle -{\frac {57}{52\,780\,000}}\,{\frac {\left(2\,n+3\right)\left(10\,{n}^{2}+30\,n+17\right)}{\left(n+4\right)\left(n+3\right)\left(n+2\right)}}a_{n+1}}
−
1
6
597
500
000
(
5
n
+
11
)
(
5
n
+
7
)
(
5
n
+
3
)
(
5
n
−
1
)
(
n
+
4
)
(
n
+
3
)
(
n
+
2
)
(
n
+
1
)
a
n
.
{\displaystyle -{\frac {1}{6\,597\,500\,000}}\,{\frac {\left(5\,n+11\right)\left(5\,n+7\right)\left(5\,n+3\right)\left(5\,n-1\right)}{\left(n+4\right)\left(n+3\right)\left(n+2\right)\left(n+1\right)}}a_{n}.}
Для комплексных значений t таких, что |t - 57| < 58, получим
BR
(
t
)
=
∑
n
=
0
∞
a
n
(
t
−
57
)
n
,
{\displaystyle \operatorname {BR} (t)=\sum _{n=0}^{\infty }a_{n}(t-57)^{n},}
что можно аналитически продолжить, о чём было уже упомянуто.
Корни x 5 — 5x — 4t = 0 можно теперь выразить в терминах корней Бринга таким образом:
r
n
=
i
−
n
BR
(
i
n
t
)
{\displaystyle r_{n}=i^{-n}\operatorname {BR} (i^{n}t)}
для n от 0 до 3, и
r
4
=
−
r
0
−
r
1
−
r
2
−
r
3
{\displaystyle r_{4}=-r_{0}-r_{1}-r_{2}-r_{3}}
для пятого корня.
Решение общего уравнения пятой степени [ править | править код ] Мы можем теперь выразить корни полинома
x
5
+
p
x
+
q
=
0
{\displaystyle x^{5}+px+q=0}
в терминах радикалов Бринга как
x
=
p
4
⋅
B
R
(
q
p
5
4
)
=
p
4
⋅
H
(
p
4
⋅
e
2
π
i
k
5
q
5
)
,
k
=
0..4
{\displaystyle x={\sqrt[{4}]{p}}\cdot BR\left({\frac {q}{\sqrt[{4}]{p^{5}}}}\right)={\sqrt[{4}]{p}}\cdot H\left({\frac {{\sqrt[{4}]{p}}\cdot e^{\frac {2\pi ik}{5}}}{\sqrt[{5}]{q}}}\right),k=0..4}
для подсчёта корня достаточно брать только 1 значение
p
4
{\displaystyle {\sqrt[{4}]{p}}}
B
R
(
x
)
=
H
(
e
2
π
i
k
5
x
5
)
,
k
=
0...4
{\displaystyle BR(x)=H\left({\frac {e^{\frac {2\pi ik}{5}}}{\sqrt[{5}]{x}}}\right),k=0...4}
Итак, у нас есть сведение к форме Бринга-Жерара в терминах разрешимых полиномиальных уравнений, при этом используются полиномиальные преобразования, включающие выражения в корнях не выше четвёртой степени. Это значит, что преобразования могут быть обращены нахождением корней многочлена, выраженных в радикалах. Эта процедура порождает лишние решения, но если отсечь их численными методами, то получим выражение для корней уравнения пятой степени через квадратные, кубические корни и радикалы Бринга, что т.о. будет алгебраическим решением в терминах алгебраических функций одной переменной - алгебраическим решением общего уравнения пятой степени.
1)
x
5
+
2
x
+
7
=
0
{\displaystyle x^{5}+2x+7=0}
x
=
2
4
⋅
B
R
(
7
2
2
4
)
=
2
4
⋅
H
(
2
2
4
7
5
e
2
π
i
k
5
)
,
k
=
0...4
{\displaystyle x={\sqrt[{4}]{2}}\cdot BR\left({\frac {7}{2{\sqrt[{4}]{2}}}}\right)={\sqrt[{4}]{2}}\cdot H\left({\sqrt[{5}]{\frac {2{\sqrt[{4}]{2}}}{7}}}e^{\frac {2\pi ik}{5}}\right),k=0...4}
2)
x
5
−
x
+
7
=
0
{\displaystyle x^{5}-x+7=0}
x
=
−
−
1
4
B
R
(
7
−
1
4
)
=
−
e
π
i
4
⋅
B
R
(
7
e
π
i
4
)
=
−
e
π
i
4
⋅
H
(
e
π
i
20
7
5
e
2
π
i
k
5
)
,
k
=
0...4
{\displaystyle x=-{\sqrt[{4}]{-1}}BR\left({\frac {7}{\sqrt[{4}]{-1}}}\right)=-e^{\frac {\pi i}{4}}\cdot BR\left({\frac {7}{e^{\frac {\pi i}{4}}}}\right)=-e^{\frac {\pi i}{4}}\cdot H\left({\frac {e^{\frac {\pi i}{20}}}{\sqrt[{5}]{7}}}e^{\frac {2\pi ik}{5}}\right),k=0...4}
функция
H
(
x
)
{\displaystyle H(x)}
3)
x
5
−
5
2
x
−
26
=
0
{\displaystyle x^{5}-{\frac {5}{2}}x-26=0}
x
k
=
e
2
π
i
k
5
(
2
+
2
−
2
)
2
(
−
2
+
2
+
2
)
2
5
+
e
4
π
i
k
5
(
−
2
+
2
+
2
)
2
(
2
−
2
−
2
)
2
5
+
{\displaystyle x_{k}=e^{\frac {2\pi ik}{5}}{\sqrt[{5}]{\frac {\left({\sqrt {2}}+{\sqrt {2-{\sqrt {2}}}}\right)^{2}\left(-{\sqrt {2}}+{\sqrt {2+{\sqrt {2}}}}\right)}{2}}}+e^{\frac {4\pi ik}{5}}{\sqrt[{5}]{\frac {\left(-{\sqrt {2}}+{\sqrt {2+{\sqrt {2}}}}\right)^{2}\left({\sqrt {2}}-{\sqrt {2-{\sqrt {2}}}}\right)}{2}}}+}
+
e
6
π
i
k
5
(
−
2
+
2
−
2
)
2
(
2
+
2
−
2
)
2
5
+
e
8
π
i
k
5
(
2
−
2
−
2
)
2
(
−
2
−
2
+
2
)
2
5
,
k
=
0
,
1
,
2
,
3
,
4
{\displaystyle +e^{\frac {6\pi ik}{5}}{\sqrt[{5}]{\frac {\left(-{\sqrt {2}}+{\sqrt {2-{\sqrt {2}}}}\right)^{2}\left({\sqrt {2}}+{\sqrt {2-{\sqrt {2}}}}\right)}{2}}}+e^{\frac {8\pi ik}{5}}{\sqrt[{5}]{\frac {\left({\sqrt {2}}-{\sqrt {2-{\sqrt {2}}}}\right)^{2}\left(-{\sqrt {2}}-{\sqrt {2+{\sqrt {2}}}}\right)}{2}}},k=0,1,2,3,4}
4)
x
5
−
5
x
+
12
=
0
{\displaystyle x^{5}-5x+12=0}
x
k
=
−
5
4
⋅
e
π
i
4
⋅
B
R
(
2
5
5
4
⋅
e
π
i
4
)
{\displaystyle x_{k}=-{\sqrt[{4}]{5}}\cdot e^{\frac {\pi i}{4}}\cdot BR\left({\frac {2}{5{\sqrt[{4}]{5}}\cdot e^{\frac {\pi i}{4}}}}\right)}
x
k
=
5
−
2
5
e
2
π
i
k
5
(
5
+
5
−
5
)
2
(
−
5
+
5
+
5
)
5
+
e
4
π
i
k
5
5
−
2
5
(
−
5
+
5
+
5
)
2
(
5
−
5
−
5
)
5
+
{\displaystyle x_{k}=5^{-{\frac {2}{5}}}e^{\frac {2\pi ik}{5}}{\sqrt[{5}]{\left({\sqrt {5}}+{\sqrt {5-{\sqrt {5}}}}\right)^{2}\left(-{\sqrt {5}}+{\sqrt {5+{\sqrt {5}}}}\right)}}+e^{\frac {4\pi ik}{5}}5^{-{\frac {2}{5}}}{\sqrt[{5}]{\left(-{\sqrt {5}}+{\sqrt {5+{\sqrt {5}}}}\right)^{2}\left({\sqrt {5}}-{\sqrt {5-{\sqrt {5}}}}\right)}}+}
+
5
−
2
5
e
6
π
i
k
5
(
−
5
−
5
+
5
)
2
(
5
+
5
−
5
)
5
+
e
8
π
i
k
5
5
−
2
5
(
5
−
5
−
5
)
2
(
−
5
−
5
+
5
)
5
,
k
=
0
,
1
,
2
,
3
,
4
{\displaystyle +5^{-{\frac {2}{5}}}e^{\frac {6\pi ik}{5}}{\sqrt[{5}]{\left(-{\sqrt {5}}-{\sqrt {5+{\sqrt {5}}}}\right)^{2}\left({\sqrt {5}}+{\sqrt {5-{\sqrt {5}}}}\right)}}+e^{\frac {8\pi ik}{5}}5^{-{\frac {2}{5}}}{\sqrt[{5}]{\left({\sqrt {5}}-{\sqrt {5-{\sqrt {5}}}}\right)^{2}\left(-{\sqrt {5}}-{\sqrt {5+{\sqrt {5}}}}\right)}},k=0,1,2,3,4}
5)
x
5
+
15
−
20
π
π
+
1
x
−
44
+
8
π
π
+
1
=
0
{\displaystyle x^{5}+{\frac {15-20{\sqrt {\pi }}}{\pi +1}}x-{\frac {44+8{\sqrt {\pi }}}{\pi +1}}=0}
x
k
=
e
2
π
i
k
5
(
π
+
1
+
π
+
1
−
π
+
1
)
2
(
−
π
+
1
+
π
+
1
+
π
+
1
)
(
π
+
1
)
2
5
+
e
4
π
i
k
5
(
−
π
+
1
+
π
+
1
+
π
+
1
)
2
(
+
π
+
1
−
π
+
1
−
π
+
1
)
(
π
+
1
)
2
5
+
{\displaystyle x_{k}=e^{\frac {2\pi ik}{5}}{\sqrt[{5}]{\frac {\left({\sqrt {\pi +1}}+{\sqrt {\pi +1-{\sqrt {\pi +1}}}}\right)^{2}\left(-{\sqrt {\pi +1}}+{\sqrt {\pi +1+{\sqrt {\pi +1}}}}\right)}{(\pi +1)^{2}}}}+e^{\frac {4\pi ik}{5}}{\sqrt[{5}]{\frac {\left(-{\sqrt {\pi +1}}+{\sqrt {\pi +1+{\sqrt {\pi +1}}}}\right)^{2}\left(+{\sqrt {\pi +1}}-{\sqrt {\pi +1-{\sqrt {\pi +1}}}}\right)}{(\pi +1)^{2}}}}+}
+
e
6
π
i
k
5
(
−
π
+
1
−
π
+
1
+
π
+
1
)
2
(
+
π
+
1
+
π
+
1
−
π
+
1
)
(
π
+
1
)
2
5
+
+
e
8
π
i
k
5
(
+
π
+
1
−
π
+
1
−
π
+
1
)
2
(
−
π
+
1
−
π
+
1
+
π
+
1
)
(
π
+
1
)
2
5
,
k
=
0
,
1
,
2
,
3
,
4.
{\displaystyle +e^{\frac {6\pi ik}{5}}{\sqrt[{5}]{\frac {\left(-{\sqrt {\pi +1}}-{\sqrt {\pi +1+{\sqrt {\pi +1}}}}\right)^{2}\left(+{\sqrt {\pi +1}}+{\sqrt {\pi +1-{\sqrt {\pi +1}}}}\right)}{(\pi +1)^{2}}}}++e^{\frac {8\pi ik}{5}}{\sqrt[{5}]{\frac {\left(+{\sqrt {\pi +1}}-{\sqrt {\pi +1-{\sqrt {\pi +1}}}}\right)^{2}\left(-{\sqrt {\pi +1}}-{\sqrt {\pi +1+{\sqrt {\pi +1}}}}\right)}{(\pi +1)^{2}}}},k=0,1,2,3,4.}
6)
x
5
+
15
x
−
44
=
0
{\displaystyle x^{5}+15x-44=0}
x
k
=
e
2
π
i
5
2
−
1
5
+
e
4
π
i
5
3
−
2
2
5
+
e
6
π
i
5
3
+
2
2
5
−
e
8
π
i
5
2
+
1
5
,
k
=
0
,
1
,
2
,
3
,
4.
{\displaystyle x_{k}=e^{\frac {2\pi i}{5}}{\sqrt[{5}]{{\sqrt {2}}-1}}+e^{\frac {4\pi i}{5}}{\sqrt[{5}]{3-2{\sqrt {2}}}}+e^{\frac {6\pi i}{5}}{\sqrt[{5}]{3+2{\sqrt {2}}}}-e^{\frac {8\pi i}{5}}{\sqrt[{5}]{{\sqrt {2}}+1}},k=0,1,2,3,4.}
Для классификации введём дискриминант
D
=
256
p
5
+
3125
q
4
{\displaystyle D=256p^{5}+3125q^{4}}
Тогда в зависимости от знака D тип графика можно разбить на 3 случая:
D
>
0
{\displaystyle D>0}
. 1 действительный корень и 4 комплексных корня. Максимум и минимум (если существуют) находятся по одну сторону от оси OX
D
<
0
{\displaystyle D<0}
. 3 действительных корня и два комплексных. Максимум и минимум находятся по разные стороны от оси OX
D
=
0
{\displaystyle D=0}
. Максимум и минимум (если существуют) находятся по одну сторону от оси OX. Полином имеет кратные корни. Их можно найти по формуле:
g
c
d
(
x
5
+
p
x
+
q
,
5
x
4
+
p
)
{\displaystyle gcd(x^{5}+px+q,5x^{4}+p)}
, где
g
c
d
(
x
,
y
)
{\displaystyle gcd(x,y)}
—
наибольший общий делитель .
Если
D
256
p
4
=
0
{\displaystyle {\frac {D}{256p^{4}}}=0}
Разрешимые классы уравнений 5 степени [ править | править код ] 1)
x
5
+
5
a
x
3
+
5
a
2
x
+
b
=
0
{\displaystyle x^{5}+5ax^{3}+5a^{2}x+b=0}
x
k
=
e
2
π
i
k
5
b
2
+
4
a
5
−
b
2
5
−
a
e
2
π
i
k
5
b
2
+
4
a
5
−
b
2
5
{\displaystyle x_{k}=e^{\frac {2\pi ik}{5}}{\sqrt[{5}]{\frac {{\sqrt {b^{2}+4a^{5}}}-b}{2}}}-{\frac {a}{e^{\frac {2\pi ik}{5}}{\sqrt[{5}]{\frac {{\sqrt {b^{2}+4a^{5}}}-b}{2}}}}}}
2)
x
5
+
a
x
+
b
{\displaystyle x^{5}+ax+b}
a
,
b
∈
Q
,
∃
ε
=
±
1
,
∃
e
≠
0
,
∃
c
>
0
{\displaystyle a,b\in Q,\exists \varepsilon =\pm 1,\exists e\neq 0,\exists c>0}
a
=
5
e
4
(
3
−
4
ϵ
c
)
c
2
+
1
,
b
=
−
4
e
5
(
11
ϵ
+
2
c
)
c
2
+
1
,
{\displaystyle a={\frac {5e^{4}(3-4\epsilon c)}{c^{2}+1}},b={\frac {-4e^{5}(11\epsilon +2c)}{c^{2}+1}},}
x
j
=
e
(
ω
j
u
1
+
ω
2
j
u
2
+
ω
3
j
u
3
+
ω
4
j
u
4
)
,
j
=
0
,
1
,
2
,
3
,
4
{\displaystyle x_{j}=e(\omega ^{j}u_{1}+\omega ^{2j}u_{2}+\omega ^{3j}u_{3}+\omega ^{4j}u_{4}),j=0,1,2,3,4}
ω
=
e
2
π
i
5
{\displaystyle \omega =e^{\frac {2\pi i}{5}}}
D
=
c
2
+
1
{\displaystyle D=c^{2}+1}
u
1
=
(
D
+
D
−
ε
D
)
2
(
−
D
+
D
−
ε
D
)
D
2
5
{\displaystyle u_{1}={\sqrt[{5}]{\frac {\left({\sqrt {D}}+{\sqrt {D-\varepsilon {\sqrt {D}}}}\right)^{2}\left(-{\sqrt {D}}+{\sqrt {D-\varepsilon {\sqrt {D}}}}\right)}{D^{2}}}}}
u
2
=
(
−
D
+
D
−
ε
D
)
2
(
D
−
D
−
ε
D
)
D
2
5
{\displaystyle u_{2}={\sqrt[{5}]{\frac {\left(-{\sqrt {D}}+{\sqrt {D-\varepsilon {\sqrt {D}}}}\right)^{2}\left({\sqrt {D}}-{\sqrt {D-\varepsilon {\sqrt {D}}}}\right)}{D^{2}}}}}
u
3
=
(
−
D
−
D
−
ε
D
)
2
(
D
+
D
−
ε
D
)
D
2
5
{\displaystyle u_{3}={\sqrt[{5}]{\frac {\left(-{\sqrt {D}}-{\sqrt {D-\varepsilon {\sqrt {D}}}}\right)^{2}\left({\sqrt {D}}+{\sqrt {D-\varepsilon {\sqrt {D}}}}\right)}{D^{2}}}}}
u
4
=
(
D
−
D
−
ε
D
)
2
(
−
D
−
D
−
ε
D
)
D
2
5
{\displaystyle u_{4}={\sqrt[{5}]{\frac {\left({\sqrt {D}}-{\sqrt {D-\varepsilon {\sqrt {D}}}}\right)^{2}\left(-{\sqrt {D}}-{\sqrt {D-\varepsilon {\sqrt {D}}}}\right)}{D^{2}}}}}
Много других свойств корней Бринга было получено, первые были сформулированы в терминах модулярных эллиптических функций Шарлем Эрмитом в 1858. Напишем основные свойства:
0.
BR
(
−
a
)
=
−
BR
(
a
)
{\displaystyle \operatorname {BR} (-a)=-\operatorname {BR} (a)}
BR
(
i
a
)
=
i
BR
(
a
)
{\displaystyle \operatorname {BR} (ia)=i\operatorname {BR} (a)}
BR
(
a
5
+
a
)
=
−
a
{\displaystyle \operatorname {BR} (a^{5}+a)=-a}
lim
n
→
∞
B
R
(
n
)
=
n
5
{\displaystyle \lim _{n\to \infty }BR(n)={\sqrt[{5}]{n}}}
BR
(
m
5
+
m
n
4
n
5
)
=
−
m
n
{\displaystyle \operatorname {BR} \left({\frac {m^{5}+mn^{4}}{n^{5}}}\right)=-{\frac {m}{n}}}
B
R
(
x
)
′
=
−
1
5
B
R
(
x
)
4
+
1
{\displaystyle BR(x)'={\frac {-1}{5BR(x)^{4}+1}}}
∫
−
1
5
B
R
(
x
)
4
+
1
d
x
=
B
R
(
x
)
+
C
{\displaystyle \int {\frac {-1}{5BR(x)^{4}+1}}dx=BR(x)+C}
x
5
+
p
x
+
q
=
0
{\displaystyle x^{5}+px+q=0}
D
=
256
p
5
+
3125
q
4
{\displaystyle D=256p^{5}+3125q^{4}}
если
p
=
3125
ϕ
χ
4
(
ϕ
−
1
)
4
(
ϕ
2
−
6
ϕ
+
25
)
,
q
=
3125
ϕ
χ
5
(
ϕ
−
1
)
4
(
ϕ
2
−
6
ϕ
+
25
)
,
ϕ
∈
R
,
χ
∈
R
{\displaystyle p={\frac {3125\phi \chi ^{4}}{(\phi -1)^{4}(\phi ^{2}-6\phi +25)}},q={\frac {3125\phi \chi ^{5}}{(\phi -1)^{4}(\phi ^{2}-6\phi +25)}},\phi \in R,\chi \in R}
то уравнение разрешимо в стандартных радикалах .
Разложение в ряд при
x
→
∞
{\displaystyle x\rightarrow \infty }
[ править | править код ] Введём:
B
r
(
x
)
=
H
(
1
x
5
)
{\displaystyle Br(x)=H\left({\frac {1}{\sqrt[{5}]{x}}}\right)}
y
=
1
x
5
{\displaystyle y={\frac {1}{\sqrt[{5}]{x}}}}
Ряд примет вид:
H
(
y
)
=
−
1
y
+
y
3
5
+
y
7
5
2
+
y
11
5
3
−
21
y
19
5
6
−
78
y
23
5
7
−
187
y
27
5
8
−
286
y
31
5
9
+
9367
y
39
5
12
+
39767
y
43
5
13
+
105672
y
47
5
14
.
.
.
{\displaystyle H(y)=-{\frac {1}{y}}+{\frac {y^{3}}{5}}+{\frac {y^{7}}{5^{2}}}+{\frac {y^{11}}{5^{3}}}-{\frac {21y^{19}}{5^{6}}}-{\frac {78y^{23}}{5^{7}}}-{\frac {187y^{27}}{5^{8}}}-{\frac {286y^{31}}{5^{9}}}+{\frac {9367y^{39}}{5^{12}}}+{\frac {39767y^{43}}{5^{13}}}+{\frac {105672y^{47}}{5^{14}}}...}
y=H(x)
B
R
(
z
)
=
H
(
1
z
5
)
=
L
(
1
z
4
5
)
z
5
{\displaystyle BR(z)=H\left({\frac {1}{\sqrt[{5}]{z}}}\right)=L\left({\frac {1}{z^{\frac {4}{5}}}}\right){\sqrt[{5}]{z}}}
Тогда:
при
z
→
∞
{\displaystyle z\rightarrow \infty }
L
(
z
)
=
−
1
+
∑
n
=
1
∞
(
−
1
)
n
j
n
z
5
n
z
,
j
1
=
1
,
j
2
=
1
,
j
3
=
5
,
j
4
=
35
,
.
.
.
{\displaystyle L(z)={\frac {-1+\displaystyle {\sum _{n=1}^{\infty }(-1)^{n}{\frac {j_{n}}{z^{5n}}}}}{z}},j_{1}=1,j_{2}=1,j_{3}=5,j_{4}=35,...}
при
z
→
0
{\displaystyle z\rightarrow 0}
L
(
z
)
=
∑
n
=
0
∞
−
3125
−
n
α
(
−
1
/
10
,
2
n
)
α
(
2
/
5
,
2
n
)
(
−
16
)
n
z
5
n
α
(
4
/
5
,
n
)
α
(
3
/
5
,
n
)
α
(
2
/
5
,
n
)
n
!
+
1
/
5
3125
−
n
α
(
4
/
5
,
2
n
)
α
(
3
/
10
,
2
n
)
(
−
16
)
n
z
5
n
+
1
α
(
6
/
5
,
n
)
α
(
4
/
5
,
n
)
α
(
3
/
5
,
n
)
n
!
+
{\displaystyle L(z)=\sum _{n=0}^{\infty }-{\frac {{3125}^{-n}\alpha \left(-1/10,2n\right)\alpha \left(2/5,2n\right)\left(-16\right)^{n}{z}^{5n}}{\alpha \left(4/5,n\right)\alpha \left(3/5,n\right)\alpha \left(2/5,n\right)n!}}+1/5{\frac {{3125}^{-n}\alpha \left(4/5,2n\right)\alpha \left(3/10,2n\right)\left(-16\right)^{n}{z}^{5n+1}}{\alpha \left(6/5,n\right)\alpha \left(4/5,n\right)\alpha \left(3/5,n\right)n!}}+}
+
1
/
25
3125
−
n
α
(
6
/
5
,
2
n
)
(
−
16
)
n
z
5
n
+
2
α
(
7
/
5
,
n
)
α
(
6
/
5
,
n
)
α
(
4
/
5
,
n
)
n
!
α
(
7
10
,
2
n
)
+
3125
−
n
α
(
8
/
5
,
2
n
)
(
−
16
)
n
z
5
n
+
3
125
α
(
8
/
5
,
n
)
α
(
7
/
5
,
n
)
α
(
6
/
5
,
n
)
n
!
α
(
11
10
,
2
n
)
{\displaystyle +1/25{{\frac {{3125}^{-n}\alpha \left(6/5,2n\right)\left(-16\right)^{n}{z}^{5n+2}}{\alpha \left(7/5,n\right)\alpha \left(6/5,n\right)\alpha \left(4/5,n\right)n!}}\alpha \left({\frac {7}{10}},2n\right)+{{\frac {{3125}^{-n}\alpha \left(8/5,2n\right)\left(-16\right)^{n}{z}^{5n+3}}{125\alpha \left(8/5,n\right)\alpha \left(7/5,n\right)\alpha \left(6/5,n\right)n!}}\alpha \left({\frac {11}{10}},2n\right)}}}
y=L(x) где
α
(
a
,
b
)
=
Γ
(
a
+
b
)
Γ
(
a
)
{\displaystyle \alpha (a,b)={\frac {\Gamma (a+b)}{\Gamma (a)}}}
Разложение в ряд при
x
→
0
{\displaystyle x\rightarrow 0}
[ править | править код ]
B
R
(
a
)
=
−
∑
k
=
0
∞
(
5
k
k
)
(
−
1
)
k
a
4
k
+
1
4
k
+
1
=
a
+
a
5
−
5
a
9
+
35
a
13
−
.
.
.
{\displaystyle BR(a)=-\sum _{k=0}^{\infty }{\binom {5k}{k}}{\frac {(-1)^{k}a^{4k+1}}{4k+1}}=a+a^{5}-5a^{9}+35a^{13}-...}
BR
(
a
)
=
−
a
4
F
3
(
1
5
,
2
5
,
3
5
,
4
5
;
1
2
,
3
4
,
5
4
;
−
5
(
5
a
4
)
4
)
{\displaystyle \operatorname {BR} (a)=-a\,\,_{4}F_{3}\left({\frac {1}{5}},{\frac {2}{5}},{\frac {3}{5}},{\frac {4}{5}};{\frac {1}{2}},{\frac {3}{4}},{\frac {5}{4}};-5\left({\frac {5a}{4}}\right)^{4}\right)}
BR
(
0
)
=
0
{\displaystyle \operatorname {BR} (0)=0}
BR
(
−
1
)
=
100
+
12
69
3
6
+
2
3
100
+
12
69
3
−
1
3
{\displaystyle \operatorname {BR} (-1)={\frac {\sqrt[{3}]{100+12{\sqrt {69}}}}{6}}+{\frac {2}{3{\sqrt[{3}]{100+12{\sqrt {69}}}}}}-{\frac {1}{3}}}
BR
(
2
)
=
−
1
{\displaystyle \operatorname {BR} (2)=-1}
Дано уравнение:
x
5
−
p
x
−
q
=
0
{\displaystyle x^{5}-px-q=0}
x
=
q
+
p
q
+
p
q
+
.
.
.
5
5
5
{\displaystyle x={\sqrt[{5}]{q+p{\sqrt[{5}]{q+p{\sqrt[{5}]{q+...}}}}}}}
x
=
lim
n
→
∞
q
+
p
q
+
.
.
.
5
5
⏞
n
{\displaystyle x=\lim _{n\to \infty }\overbrace {\sqrt[{5}]{q+p{\sqrt[{5}]{q+...}}}} ^{n}}
x
=
q
+
p
q
+
p
q
+
.
.
.
5
5
5
{\displaystyle x={\sqrt[{5}]{q+p{\sqrt[{5}]{q+p{\sqrt[{5}]{q+...}}}}}}}
1)Представим эту запись в виде последовательности
x
n
{\displaystyle x_{n}}
x
1
=
q
5
{\displaystyle x_{1}={\sqrt[{5}]{q}}}
x
2
=
q
+
p
q
5
5
{\displaystyle x_{2}={\sqrt[{5}]{q+p{\sqrt[{5}]{q}}}}}
x
n
+
1
=
q
+
p
x
n
5
{\displaystyle x_{n+1}={\sqrt[{5}]{q+px_{n}}}}
2) Эта последовательность монотонно возрастает и ограничена , значит имеет предел при
n
→
∞
{\displaystyle n\rightarrow \infty }
x
n
+
1
=
x
n
{\displaystyle x_{n+1}=x_{n}}
значит получаем уравнение:
x
=
q
+
p
x
5
{\displaystyle x={\sqrt[{5}]{q+px}}}
x
5
−
p
x
−
q
=
0
{\displaystyle x^{5}-px-q=0}
Что и требовалось доказать.
x
5
−
x
+
d
=
0
{\displaystyle x^{5}-x+d=0}
1)
k
=
tan
(
1
4
arcsin
(
16
25
5
d
2
)
)
{\displaystyle k=\tan \left({\frac {1}{4}}\arcsin \left({\frac {16}{25{\sqrt {5}}d^{2}}}\right)\right)}
K
(
x
)
=
∫
0
π
2
d
φ
1
−
x
2
sin
2
φ
{\displaystyle K(x)=\int \limits _{0}^{\frac {\pi }{2}}{\frac {d\varphi }{\sqrt {1-x^{2}\sin ^{2}\varphi }}}}
p
n
=
i
K
(
1
−
k
2
)
K
(
k
2
)
+
16
n
,
n
=
0
,
1
,
2
,
3
,
4
{\displaystyle p_{n}=i{\frac {K(1-k^{2})}{K(k^{2})}}+16n,n=0,1,2,3,4}
2) Для
j
=
0
,
1
,
2
,
3
,
4
{\displaystyle j=0,1,2,3,4}
S
j
=
(
e
π
i
4
)
j
2
η
(
τ
j
)
η
2
(
4
τ
j
)
η
3
(
2
τ
j
)
,
τ
j
=
p
n
+
2
j
10
{\displaystyle S_{j}=\left(e^{\frac {\pi i}{4}}\right)^{j}{\frac {{\sqrt {2}}\eta (\tau _{j})\eta ^{2}(4\tau _{j})}{\eta ^{3}(2\tau _{j})}},\tau _{j}={\frac {p_{n}+2j}{10}}}
η
(
x
)
=
e
π
i
x
12
∏
k
=
1
∞
(
1
−
e
2
π
i
k
x
)
{\displaystyle \eta (x)=e^{\frac {\pi ix}{12}}\prod _{k=1}^{\infty }(1-e^{2\pi ikx})}
Эта-функция Дедекинда [en]
S
5
=
2
η
(
5
p
n
2
)
η
2
(
10
p
n
)
η
3
(
5
p
n
)
.
{\displaystyle S_{5}={\frac {{\sqrt {2}}\eta \left({\frac {5p_{n}}{2}}\right)\eta ^{2}(10p_{n})}{\eta ^{3}(5p_{n})}}.}
Тогда:
x
n
=
±
1
2
⋅
5
3
4
⋅
k
2
8
k
−
k
3
⋅
(
S
0
+
S
5
)
(
S
1
+
i
S
4
)
(
i
S
2
+
S
3
)
{\displaystyle x_{n}={\frac {\pm 1}{2\cdot 5^{\frac {3}{4}}}}\cdot {\frac {k^{\frac {2}{8}}}{\sqrt {k-k^{3}}}}\cdot (S_{0}+S_{5})(S_{1}+iS_{4})(iS_{2}+S_{3})}
По М. Л. Глассеру (см. ссылку внизу) можно найти решение любого полиномиального уравнения из трёх слагаемых вида:
x
N
−
x
+
t
{\displaystyle x^{N}-x+t}
В частности, произвольное уравнение пятой степени может быть сведено к такой форме с помощью преобразований Чирнхгауза, показанных выше. Возьмём
x
=
ζ
−
1
/
(
N
−
1
)
{\displaystyle x=\zeta ^{-1/(N-1)}}
ζ
=
e
2
π
i
+
t
ϕ
(
ζ
)
,
{\displaystyle \zeta =e^{2\pi i}+t\phi (\zeta ),}
а
ϕ
(
ζ
)
=
ζ
N
/
(
N
−
1
)
{\displaystyle \phi (\zeta )=\zeta ^{N/(N-1)}}
Формула Лагранжа показывает, что любая аналитическая функция f в окрестности корня преобразованного общего уравнения относительно ζ может быть выражена в виде бесконечного ряда :
f
(
ζ
)
=
f
(
e
2
π
i
)
+
∑
n
=
1
∞
t
n
n
!
d
n
−
1
d
a
n
−
1
[
f
′
(
a
)
|
ϕ
(
a
)
|
n
]
a
=
e
2
π
i
{\displaystyle f(\zeta )=f(e^{2\pi i})+\sum _{n=1}^{\infty }{\frac {t^{n}}{n!}}{\frac {d^{n-1}}{da^{n-1}}}[f'(a)|\phi (a)|^{n}]_{a=e^{2\pi i}}}
Если мы положим
f
(
ζ
)
=
ζ
−
1
/
(
N
−
1
)
{\displaystyle f(\zeta )=\zeta ^{-1/(N-1)}}
x
1
=
exp
(
−
2
π
i
/
(
N
−
1
)
)
−
t
N
−
1
∑
n
=
0
∞
(
t
e
2
π
i
/
(
N
−
1
)
)
n
Γ
(
n
+
2
)
Γ
(
N
n
N
−
1
+
1
)
Γ
(
n
N
−
1
+
1
)
{\displaystyle x_{1}=\exp(-2\pi i/(N-1))-{\frac {t}{N-1}}\sum _{n=0}^{\infty }{\frac {(te^{2\pi i/(N-1)})^{n}}{\Gamma (n+2)}}{\frac {\Gamma ({\frac {Nn}{N-1}}+1)}{\Gamma ({\frac {n}{N-1}}+1)}}}
Следующие N-2 корня могут быть найдены заменой
exp
(
−
2
π
i
/
(
N
−
1
)
)
{\displaystyle \exp(-2\pi i/(N-1))}
корни (N-1)-й степени из единицы , а последний корень - из теоремы Виета (например, используя тот факт, что сумма всех корней многочлена трёхчленной формы, приведённой выше, равна 1). С помощью теоремы умножения Гаусса [en] гипергеометрических функций :
ψ
(
q
)
=
(
ω
t
N
−
1
)
q
n
q
N
/
(
N
−
1
)
∏
k
=
0
N
−
1
Γ
(
N
q
/
(
N
−
1
)
+
1
+
k
N
)
Γ
(
q
N
−
1
+
1
)
∏
k
=
0
N
−
2
Γ
(
q
+
k
+
2
N
−
1
)
{\displaystyle \psi (q)=({\frac {\omega t}{N-1}})^{q}n^{qN/(N-1)}{\frac {\prod _{k=0}^{N-1}\Gamma ({\frac {Nq/(N-1)+1+k}{N}})}{\Gamma ({\frac {q}{N-1}}+1)\prod _{k=0}^{N-2}\Gamma ({\frac {q+k+2}{N-1}})}}}
x
1
=
ω
−
1
−
t
(
N
−
1
)
2
N
2
π
(
N
−
1
)
∑
q
=
0
N
−
2
ψ
(
q
)
N
+
1
F
N
[
q
N
/
(
N
−
1
)
+
1
N
,
…
,
q
N
/
(
N
−
1
)
+
N
N
,
1
;
q
+
2
N
−
1
,
…
,
q
+
N
N
−
1
,
q
N
−
1
+
1
;
(
t
ω
N
−
1
)
N
−
1
N
N
)
]
{\displaystyle x_{1}=\omega ^{-1}-{\frac {t}{(N-1)^{2}}}{\sqrt {\frac {N}{2\pi (N-1)}}}\sum _{q=0}^{N-2}\psi (q)_{N+1}F_{N}{\begin{bmatrix}{\frac {qN/(N-1)+1}{N}},\ldots ,{\frac {qN/(N-1)+N}{N}},1;\\{\frac {q+2}{N-1}},\ldots ,{\frac {q+N}{N-1}},{\frac {q}{N-1}}+1;\\({\frac {t\omega }{N-1}})^{N-1}N^{N})\end{bmatrix}}}
где
ω
=
exp
(
2
π
i
/
(
N
−
1
)
)
{\displaystyle \omega =\exp(2\pi i/(N-1))}
a
x
N
+
b
x
2
+
c
=
0
,
N
≡
1
(
mod
2
)
{\displaystyle {}_{ax^{N}+bx^{2}+c=0,N\equiv 1{\pmod {2}}}}
x
N
=
−
a
2
b
(
c
b
)
N
−
1
N
−
1
F
N
−
2
[
N
+
1
2
N
,
N
+
3
2
N
,
⋯
,
N
−
2
N
,
N
−
1
N
,
N
+
1
N
,
N
+
2
N
,
⋯
,
3
N
−
3
2
N
,
3
N
−
1
2
N
;
N
+
1
2
N
−
4
,
N
+
3
2
N
−
4
,
⋯
,
N
−
4
N
−
2
,
N
−
3
N
−
2
,
N
−
1
N
−
2
,
N
N
−
2
,
⋯
,
3
N
−
5
2
N
−
4
,
3
2
;
−
a
2
c
N
−
2
4
b
N
(
N
−
2
)
N
−
2
]
+
c
b
i
N
−
1
F
N
−
2
[
1
2
N
,
3
2
N
,
⋯
,
N
−
4
2
N
,
N
−
2
2
N
,
N
+
2
2
N
,
N
+
4
2
N
,
⋯
,
2
N
−
3
2
N
,
2
N
−
1
2
N
;
3
2
N
−
4
,
5
2
N
−
4
,
⋯
,
2
N
−
3
2
N
−
4
;
−
a
2
c
N
−
2
4
b
N
(
N
−
2
)
N
−
2
]
{\displaystyle {}_{x_{N}=-{\frac {a}{2b}}{\sqrt {\left({\frac {c}{b}}\right)^{N-1}}}{}_{N-1}F_{N-2}{\begin{bmatrix}{\frac {N+1}{2N}},{\frac {N+3}{2N}},\cdots ,{\frac {N-2}{N}},{\frac {N-1}{N}},{\frac {N+1}{N}},{\frac {N+2}{N}},\cdots ,{\frac {3N-3}{2N}},{\frac {3N-1}{2N}};\\[8pt]{\frac {N+1}{2N-4}},{\frac {N+3}{2N-4}},\cdots ,{\frac {N-4}{N-2}},{\frac {N-3}{N-2}},{\frac {N-1}{N-2}},{\frac {N}{N-2}},\cdots ,{\frac {3N-5}{2N-4}},{\frac {3}{2}};\\[8pt]-{\frac {a^{2}c^{N-2}}{4b^{N}\left(N-2\right)^{N-2}}}\end{bmatrix}}+{\sqrt {\frac {c}{b}}}{\rm {i}}{}_{N-1}F_{N-2}{\begin{bmatrix}{\frac {1}{2N}},{\frac {3}{2N}},\cdots ,{\frac {N-4}{2N}},{\frac {N-2}{2N}},{\frac {N+2}{2N}},{\frac {N+4}{2N}},\cdots ,{\frac {2N-3}{2N}},{\frac {2N-1}{2N}};\\[8pt]{\frac {3}{2N-4}},{\frac {5}{2N-4}},\cdots ,{\frac {2N-3}{2N-4}};\\[8pt]-{\frac {a^{2}c^{N-2}}{4b^{N}\left(N-2\right)^{N-2}}}\end{bmatrix}}}}
x
N
−
1
=
−
a
2
b
(
c
b
)
N
−
1
N
−
1
F
N
−
2
[
N
+
1
2
N
,
N
+
3
2
N
,
⋯
,
N
−
2
N
,
N
−
1
N
,
N
+
1
N
,
N
+
2
N
,
⋯
,
3
N
−
3
2
N
,
3
N
−
1
2
N
;
N
+
1
2
N
−
4
,
N
+
3
2
N
−
4
,
⋯
,
N
−
4
N
−
2
,
N
−
3
N
−
2
,
N
−
1
N
−
2
,
N
N
−
2
,
⋯
,
3
N
−
5
2
N
−
4
,
3
2
;
−
a
2
c
N
−
2
4
b
N
(
N
−
2
)
N
−
2
]
−
c
b
i
N
−
1
F
N
−
2
[
1
2
N
,
3
2
N
,
⋯
,
N
−
4
2
N
,
N
−
2
2
N
,
N
+
2
2
N
,
N
+
4
2
N
,
⋯
,
2
N
−
3
2
N
,
2
N
−
1
2
N
;
3
2
N
−
4
,
5
2
N
−
4
,
⋯
,
2
N
−
3
2
N
−
4
;
−
a
2
c
N
−
2
4
b
N
(
N
−
2
)
N
−
2
]
{\displaystyle {}_{x_{N-1}=-{\frac {a}{2b}}{\sqrt {\left({\frac {c}{b}}\right)^{N-1}}}{}_{N-1}F_{N-2}{\begin{bmatrix}{\frac {N+1}{2N}},{\frac {N+3}{2N}},\cdots ,{\frac {N-2}{N}},{\frac {N-1}{N}},{\frac {N+1}{N}},{\frac {N+2}{N}},\cdots ,{\frac {3N-3}{2N}},{\frac {3N-1}{2N}};\\[8pt]{\frac {N+1}{2N-4}},{\frac {N+3}{2N-4}},\cdots ,{\frac {N-4}{N-2}},{\frac {N-3}{N-2}},{\frac {N-1}{N-2}},{\frac {N}{N-2}},\cdots ,{\frac {3N-5}{2N-4}},{\frac {3}{2}};\\[8pt]-{\frac {a^{2}c^{N-2}}{4b^{N}\left(N-2\right)^{N-2}}}\end{bmatrix}}-{\sqrt {\frac {c}{b}}}{\rm {i}}{}_{N-1}F_{N-2}{\begin{bmatrix}{\frac {1}{2N}},{\frac {3}{2N}},\cdots ,{\frac {N-4}{2N}},{\frac {N-2}{2N}},{\frac {N+2}{2N}},{\frac {N+4}{2N}},\cdots ,{\frac {2N-3}{2N}},{\frac {2N-1}{2N}};\\[8pt]{\frac {3}{2N-4}},{\frac {5}{2N-4}},\cdots ,{\frac {2N-3}{2N-4}};\\[8pt]-{\frac {a^{2}c^{N-2}}{4b^{N}\left(N-2\right)^{N-2}}}\end{bmatrix}}}}
x
n
=
−
e
2
n
π
i
N
−
2
b
a
N
−
2
N
−
1
F
N
−
2
[
−
1
N
(
N
−
2
)
,
−
1
N
(
N
−
2
)
+
1
N
,
−
1
N
(
N
−
2
)
+
2
N
,
⋯
,
−
1
N
(
N
−
2
)
+
1
N
,
N
−
5
2
N
,
−
1
N
(
N
−
2
)
+
N
−
3
2
N
,
−
1
N
(
N
−
2
)
+
N
+
1
2
N
,
−
1
N
(
N
−
2
)
+
N
+
3
2
N
,
⋯
,
−
1
N
(
N
−
2
)
+
N
−
1
N
,
;
1
N
−
2
,
2
N
−
2
,
⋯
,
2
N
−
5
2
N
−
4
,
;
−
a
2
c
N
−
2
4
b
N
(
N
−
2
)
N
−
2
]
+
b
a
N
−
2
∑
q
=
1
N
−
3
Γ
(
2
q
−
1
N
−
2
+
q
)
Γ
(
2
q
−
1
N
−
2
+
1
)
⋅
(
−
c
b
a
2
b
2
N
−
2
)
q
⋅
e
2
n
(
1
−
2
q
)
N
−
2
π
i
q
!
N
−
1
F
N
−
2
[
N
q
−
1
N
(
N
−
2
)
,
N
q
−
1
N
(
N
−
2
)
+
1
N
,
N
q
−
1
N
(
N
−
2
)
+
2
N
,
⋯
,
N
q
−
1
N
(
N
−
2
)
+
N
−
3
2
N
,
N
q
−
1
N
(
N
−
2
)
+
N
+
1
2
N
,
⋯
,
N
q
−
1
N
(
N
−
2
)
+
N
−
1
N
;
q
+
1
N
−
2
,
q
+
2
N
−
2
,
⋯
,
N
−
4
N
−
2
,
N
−
3
N
−
2
,
N
−
1
N
−
2
,
N
N
−
2
,
⋯
,
q
+
N
−
2
N
−
2
,
2
q
+
2
N
−
5
2
N
−
4
;
−
a
2
c
N
−
2
4
b
N
(
N
−
2
)
N
−
2
]
,
n
=
1
,
2
,
⋯
,
N
−
2
{\displaystyle {}_{x_{n}=-e^{\frac {2n\pi {\rm {i}}}{N-2}}{\sqrt[{N-2}]{\frac {b}{a}}}{}_{N-1}F_{N-2}{\begin{bmatrix}-{\frac {1}{N\left(N-2\right)}},-{\frac {1}{N\left(N-2\right)}}+{\frac {1}{N}},-{\frac {1}{N\left(N-2\right)}}+{\frac {2}{N}},\cdots ,-{\frac {1}{N\left(N-2\right)}}+{\frac {1}{N}},{\frac {N-5}{2N}},-{\frac {1}{N\left(N-2\right)}}+{\frac {N-3}{2N}},-{\frac {1}{N\left(N-2\right)}}+{\frac {N+1}{2N}},-{\frac {1}{N\left(N-2\right)}}+{\frac {N+3}{2N}},\cdots ,-{\frac {1}{N\left(N-2\right)}}+{\frac {N-1}{N}},;\\[8pt]{\frac {1}{N-2}},{\frac {2}{N-2}},\cdots ,{\frac {2N-5}{2N-4}},;\\[8pt]-{\frac {a^{2}c^{N-2}}{4b^{N}\left(N-2\right)^{N-2}}}\end{bmatrix}}+{\sqrt[{N-2}]{\frac {b}{a}}}\sum _{q=1}^{N-3}{\frac {\Gamma \left({\frac {2q-1}{N-2}}+q\right)}{\Gamma \left({\frac {2q-1}{N-2}}+1\right)}}\cdot \left(-{\frac {c}{b}}{\sqrt[{N-2}]{\frac {a^{2}}{b^{2}}}}\right)^{q}\cdot {\frac {e^{{\frac {2n\left(1-2q\right)}{N-2}}\pi {\rm {i}}}}{q!}}{}_{N-1}F_{N-2}{\begin{bmatrix}{\frac {Nq-1}{N\left(N-2\right)}},{\frac {Nq-1}{N\left(N-2\right)}}+{\frac {1}{N}},{\frac {Nq-1}{N\left(N-2\right)}}+{\frac {2}{N}},\cdots ,{\frac {Nq-1}{N\left(N-2\right)}}+{\frac {N-3}{2N}},{\frac {Nq-1}{N\left(N-2\right)}}+{\frac {N+1}{2N}},\cdots ,{\frac {Nq-1}{N\left(N-2\right)}}+{\frac {N-1}{N}};\\[8pt]{\frac {q+1}{N-2}},{\frac {q+2}{N-2}},\cdots ,{\frac {N-4}{N-2}},{\frac {N-3}{N-2}},{\frac {N-1}{N-2}},{\frac {N}{N-2}},\cdots ,{\frac {q+N-2}{N-2}},{\frac {2q+2N-5}{2N-4}};\\[8pt]-{\frac {a^{2}c^{N-2}}{4b^{N}\left(N-2\right)^{N-2}}}\end{bmatrix}},n=1,2,\cdots ,N-2}}
Корни уравнения тогда можно представить как сумму самое большее N-1 гипергеометрических функций. Применяя этот метод к редуцированной форме Бринга-Жеррара, определим следующие функции:
F
1
(
t
)
=
F
2
(
t
)
F
2
(
t
)
=
4
F
3
(
1
/
5
,
2
/
5
,
3
/
5
,
4
/
5
;
1
/
2
,
3
/
4
,
5
/
4
;
3125
t
4
/
256
)
F
3
(
t
)
=
4
F
3
(
9
/
20
,
13
/
20
,
17
/
20
,
21
/
20
;
3
/
4
,
5
/
4
,
3
/
2
;
3125
t
4
/
256
)
F
4
(
t
)
=
4
F
3
(
7
/
10
,
9
/
10
,
11
/
10
,
13
/
10
;
5
/
4
,
3
/
2
,
7
/
4
;
3125
t
4
/
256
)
{\displaystyle {\begin{matrix}F_{1}(t)&=&F_{2}(t)\\F_{2}(t)&=&\,_{4}F_{3}(1/5,&2/5,&3/5,&4/5;&1/2,&3/4,&5/4;&3125t^{4}/256)\\F_{3}(t)&=&\,_{4}F_{3}(9/20,&13/20,&17/20,&21/20;&3/4,&5/4,&3/2;&3125t^{4}/256)\\F_{4}(t)&=&\,_{4}F_{3}(7/10,&9/10,&11/10,&13/10;&5/4,&3/2,&7/4;&3125t^{4}/256)\end{matrix}}}
которые суть гипергеометрические функции, присутствующие в рядах выше. Корни уравнения пятой степени тогда:
x
1
=
−
t
4
F
1
(
t
)
x
2
=
−
F
1
(
t
)
+
1
4
t
F
2
(
t
)
+
5
32
t
2
F
3
(
t
)
+
5
32
t
3
F
3
(
t
)
x
3
=
−
F
1
(
t
)
+
1
4
t
F
2
(
t
)
−
5
32
t
2
F
3
(
t
)
+
5
32
t
3
F
3
(
t
)
x
4
=
−
i
F
1
(
t
)
+
1
4
t
F
2
(
t
)
−
5
32
i
t
2
F
3
(
t
)
−
5
32
t
3
F
3
(
t
)
x
5
=
i
F
1
(
t
)
+
1
4
t
F
2
(
t
)
+
5
32
i
t
2
F
3
(
t
)
−
5
32
t
3
F
3
(
t
)
{\displaystyle {\begin{matrix}x_{1}&=&-t^{4}F_{1}(t)\\x_{2}&=&-F_{1}(t)&+{\frac {1}{4}}tF_{2}(t)&+{\frac {5}{32}}t^{2}F_{3}(t)&+{\frac {5}{32}}t^{3}F_{3}(t)\\x_{3}&=&-F_{1}(t)&+{\frac {1}{4}}tF_{2}(t)&-{\frac {5}{32}}t^{2}F_{3}(t)&+{\frac {5}{32}}t^{3}F_{3}(t)\\x_{4}&=&-iF_{1}(t)&+{\frac {1}{4}}tF_{2}(t)&-{\frac {5}{32}}it^{2}F_{3}(t)&-{\frac {5}{32}}t^{3}F_{3}(t)\\x_{5}&=&iF_{1}(t)&+{\frac {1}{4}}tF_{2}(t)&+{\frac {5}{32}}it^{2}F_{3}(t)&-{\frac {5}{32}}t^{3}F_{3}(t)\\\end{matrix}}}
Это по существу тот же результат, что был получен методом дифференциальной резольвенты , разработанным Джеймсом Коклом [en] 1860 году .
f
[
ϕ
(
a
)
]
=
0
{\displaystyle f[\phi (a)]=0}
Функция φ может быть определена так:
d
f
[
ϕ
(
a
)
]
d
a
=
0
d
2
f
[
ϕ
(
a
)
]
d
a
2
=
0
d
3
f
[
ϕ
(
a
)
]
d
a
3
=
0
d
4
f
[
ϕ
(
a
)
]
d
a
4
=
0
{\displaystyle {\begin{aligned}{\frac {df[\phi (a)]}{da}}=0\\[6pt]{\frac {d^{2}f[\phi (a)]}{da^{2}}}=0\\[6pt]{\frac {d^{3}f[\phi (a)]}{da^{3}}}=0\\[6pt]{\frac {d^{4}f[\phi (a)]}{da^{4}}}=0\end{aligned}}}
Тогда дифференциальная резольвента такова:
(
256
−
3125
a
4
)
1155
d
4
ϕ
d
a
4
−
6250
a
3
231
d
3
ϕ
d
a
3
−
4875
a
2
77
d
2
ϕ
d
a
2
−
2125
a
77
d
ϕ
d
a
+
ϕ
=
0
{\displaystyle {\frac {(256-3125a^{4})}{1155}}{\frac {d^{4}\phi }{da^{4}}}-{\frac {6250a^{3}}{231}}{\frac {d^{3}\phi }{da^{3}}}-{\frac {4875a^{2}}{77}}{\frac {d^{2}\phi }{da^{2}}}-{\frac {2125a}{77}}{\frac {d\phi }{da}}+\phi =0}












































![{\displaystyle x={\sqrt[{4}]{p}}\cdot BR\left({\frac {q}{\sqrt[{4}]{p^{5}}}}\right)={\sqrt[{4}]{p}}\cdot H\left({\frac {{\sqrt[{4}]{p}}\cdot e^{\frac {2\pi ik}{5}}}{\sqrt[{5}]{q}}}\right),k=0..4}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76e8c724564d5f9b6c636cb98334fcd0b432fc02)
![{\displaystyle {\sqrt[{4}]{p}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7288cc080f0204cd14dcc366f033dbcd870c896)
![{\displaystyle BR(x)=H\left({\frac {e^{\frac {2\pi ik}{5}}}{\sqrt[{5}]{x}}}\right),k=0...4}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6d67bbd70ded5b7db1ece57bcc61846a5471ef0)


![{\displaystyle \alpha ={\sqrt[{4}]{p}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/901ac0545c99fefcadaeba60cc953f1aa40a55ba)


![{\displaystyle x={\sqrt[{4}]{p}}\cdot BR\left({\frac {q}{p{\sqrt[{4}]{p}}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c63d2950560099799e27d77e5e6738338e00b76c)

![{\displaystyle x={\sqrt[{4}]{2}}\cdot BR\left({\frac {7}{2{\sqrt[{4}]{2}}}}\right)={\sqrt[{4}]{2}}\cdot H\left({\sqrt[{5}]{\frac {2{\sqrt[{4}]{2}}}{7}}}e^{\frac {2\pi ik}{5}}\right),k=0...4}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf85ef3393c0584c3d542b52db214d49161b1ffb)

![{\displaystyle x=-{\sqrt[{4}]{-1}}BR\left({\frac {7}{\sqrt[{4}]{-1}}}\right)=-e^{\frac {\pi i}{4}}\cdot BR\left({\frac {7}{e^{\frac {\pi i}{4}}}}\right)=-e^{\frac {\pi i}{4}}\cdot H\left({\frac {e^{\frac {\pi i}{20}}}{\sqrt[{5}]{7}}}e^{\frac {2\pi ik}{5}}\right),k=0...4}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b3b8a974aa42740138622efc0733fb4a5312f7d)


![{\displaystyle x_{k}=e^{\frac {2\pi ik}{5}}{\sqrt[{5}]{\frac {\left({\sqrt {2}}+{\sqrt {2-{\sqrt {2}}}}\right)^{2}\left(-{\sqrt {2}}+{\sqrt {2+{\sqrt {2}}}}\right)}{2}}}+e^{\frac {4\pi ik}{5}}{\sqrt[{5}]{\frac {\left(-{\sqrt {2}}+{\sqrt {2+{\sqrt {2}}}}\right)^{2}\left({\sqrt {2}}-{\sqrt {2-{\sqrt {2}}}}\right)}{2}}}+}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00d1ef6fd1570aa1d1793faf0b01c9fbbf28d2de)
![{\displaystyle +e^{\frac {6\pi ik}{5}}{\sqrt[{5}]{\frac {\left(-{\sqrt {2}}+{\sqrt {2-{\sqrt {2}}}}\right)^{2}\left({\sqrt {2}}+{\sqrt {2-{\sqrt {2}}}}\right)}{2}}}+e^{\frac {8\pi ik}{5}}{\sqrt[{5}]{\frac {\left({\sqrt {2}}-{\sqrt {2-{\sqrt {2}}}}\right)^{2}\left(-{\sqrt {2}}-{\sqrt {2+{\sqrt {2}}}}\right)}{2}}},k=0,1,2,3,4}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40967259687285046ef2020ad4b13044a8f318ec)

![{\displaystyle x_{k}=-{\sqrt[{4}]{5}}\cdot e^{\frac {\pi i}{4}}\cdot BR\left({\frac {2}{5{\sqrt[{4}]{5}}\cdot e^{\frac {\pi i}{4}}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6c16e563be5f4dc8e2f7351841e3297d41e49b9)
![{\displaystyle x_{k}=5^{-{\frac {2}{5}}}e^{\frac {2\pi ik}{5}}{\sqrt[{5}]{\left({\sqrt {5}}+{\sqrt {5-{\sqrt {5}}}}\right)^{2}\left(-{\sqrt {5}}+{\sqrt {5+{\sqrt {5}}}}\right)}}+e^{\frac {4\pi ik}{5}}5^{-{\frac {2}{5}}}{\sqrt[{5}]{\left(-{\sqrt {5}}+{\sqrt {5+{\sqrt {5}}}}\right)^{2}\left({\sqrt {5}}-{\sqrt {5-{\sqrt {5}}}}\right)}}+}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0cf56aa452bca28182331b8b0faf785036ce91f9)
![{\displaystyle +5^{-{\frac {2}{5}}}e^{\frac {6\pi ik}{5}}{\sqrt[{5}]{\left(-{\sqrt {5}}-{\sqrt {5+{\sqrt {5}}}}\right)^{2}\left({\sqrt {5}}+{\sqrt {5-{\sqrt {5}}}}\right)}}+e^{\frac {8\pi ik}{5}}5^{-{\frac {2}{5}}}{\sqrt[{5}]{\left({\sqrt {5}}-{\sqrt {5-{\sqrt {5}}}}\right)^{2}\left(-{\sqrt {5}}-{\sqrt {5+{\sqrt {5}}}}\right)}},k=0,1,2,3,4}](https://wikimedia.org/api/rest_v1/media/math/render/svg/499ee41c201a1785e0d4d86950da9b24bc2f9b23)

![{\displaystyle x_{k}=e^{\frac {2\pi ik}{5}}{\sqrt[{5}]{\frac {\left({\sqrt {\pi +1}}+{\sqrt {\pi +1-{\sqrt {\pi +1}}}}\right)^{2}\left(-{\sqrt {\pi +1}}+{\sqrt {\pi +1+{\sqrt {\pi +1}}}}\right)}{(\pi +1)^{2}}}}+e^{\frac {4\pi ik}{5}}{\sqrt[{5}]{\frac {\left(-{\sqrt {\pi +1}}+{\sqrt {\pi +1+{\sqrt {\pi +1}}}}\right)^{2}\left(+{\sqrt {\pi +1}}-{\sqrt {\pi +1-{\sqrt {\pi +1}}}}\right)}{(\pi +1)^{2}}}}+}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ddc5fbbf8c2970d40c4ef01fff738b870bba4d8)
![{\displaystyle +e^{\frac {6\pi ik}{5}}{\sqrt[{5}]{\frac {\left(-{\sqrt {\pi +1}}-{\sqrt {\pi +1+{\sqrt {\pi +1}}}}\right)^{2}\left(+{\sqrt {\pi +1}}+{\sqrt {\pi +1-{\sqrt {\pi +1}}}}\right)}{(\pi +1)^{2}}}}++e^{\frac {8\pi ik}{5}}{\sqrt[{5}]{\frac {\left(+{\sqrt {\pi +1}}-{\sqrt {\pi +1-{\sqrt {\pi +1}}}}\right)^{2}\left(-{\sqrt {\pi +1}}-{\sqrt {\pi +1+{\sqrt {\pi +1}}}}\right)}{(\pi +1)^{2}}}},k=0,1,2,3,4.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a35058d459836f8f15937e17f508516bf38d9ba4)

![{\displaystyle x_{k}=e^{\frac {2\pi i}{5}}{\sqrt[{5}]{{\sqrt {2}}-1}}+e^{\frac {4\pi i}{5}}{\sqrt[{5}]{3-2{\sqrt {2}}}}+e^{\frac {6\pi i}{5}}{\sqrt[{5}]{3+2{\sqrt {2}}}}-e^{\frac {8\pi i}{5}}{\sqrt[{5}]{{\sqrt {2}}+1}},k=0,1,2,3,4.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98bd3450dd4d6d61481a71825e90aa77265e69e2)











![{\displaystyle x_{k}=e^{\frac {2\pi ik}{5}}{\sqrt[{5}]{\frac {{\sqrt {b^{2}+4a^{5}}}-b}{2}}}-{\frac {a}{e^{\frac {2\pi ik}{5}}{\sqrt[{5}]{\frac {{\sqrt {b^{2}+4a^{5}}}-b}{2}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4671aeaa7c86366dc5e5783b1c149e2fee13b943)






![{\displaystyle u_{1}={\sqrt[{5}]{\frac {\left({\sqrt {D}}+{\sqrt {D-\varepsilon {\sqrt {D}}}}\right)^{2}\left(-{\sqrt {D}}+{\sqrt {D-\varepsilon {\sqrt {D}}}}\right)}{D^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25e44c21dc98ba1a95674ac1303cee95a6e61b23)
![{\displaystyle u_{2}={\sqrt[{5}]{\frac {\left(-{\sqrt {D}}+{\sqrt {D-\varepsilon {\sqrt {D}}}}\right)^{2}\left({\sqrt {D}}-{\sqrt {D-\varepsilon {\sqrt {D}}}}\right)}{D^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d117ee2dd8562fc1f9f32330de1a320b6a97fc16)
![{\displaystyle u_{3}={\sqrt[{5}]{\frac {\left(-{\sqrt {D}}-{\sqrt {D-\varepsilon {\sqrt {D}}}}\right)^{2}\left({\sqrt {D}}+{\sqrt {D-\varepsilon {\sqrt {D}}}}\right)}{D^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49402d364c07a511df43f33266ea00115f62d2c4)
![{\displaystyle u_{4}={\sqrt[{5}]{\frac {\left({\sqrt {D}}-{\sqrt {D-\varepsilon {\sqrt {D}}}}\right)^{2}\left(-{\sqrt {D}}-{\sqrt {D-\varepsilon {\sqrt {D}}}}\right)}{D^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af6652e943d691322f79962fefde8ac9e9ac849f)



![{\displaystyle \lim _{n\to \infty }BR(n)={\sqrt[{5}]{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fdad6e1cf85fd479da61c28d92489092f6b8d2e)





![{\displaystyle Br(x)=H\left({\frac {1}{\sqrt[{5}]{x}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9d4bb396f82c2589cd59b08d94674607a381a4c)
![{\displaystyle y={\frac {1}{\sqrt[{5}]{x}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e209e660552b465bcf32b03d3e59e2cb57dc147)

![{\displaystyle BR(z)=H\left({\frac {1}{\sqrt[{5}]{z}}}\right)=L\left({\frac {1}{z^{\frac {4}{5}}}}\right){\sqrt[{5}]{z}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f32854ccb672d7f6ed08df93fe8ed524f1819a1c)










![{\displaystyle \operatorname {BR} (-1)={\frac {\sqrt[{3}]{100+12{\sqrt {69}}}}{6}}+{\frac {2}{3{\sqrt[{3}]{100+12{\sqrt {69}}}}}}-{\frac {1}{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4efdc764e6a6c337b54cfb166ce28ac9cb520e1e)


![{\displaystyle x={\sqrt[{5}]{q+p{\sqrt[{5}]{q+p{\sqrt[{5}]{q+...}}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d966b9f234877c33f6f61ebc4e355e89b56b755)
![{\displaystyle x=\lim _{n\to \infty }\overbrace {\sqrt[{5}]{q+p{\sqrt[{5}]{q+...}}}} ^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b505b85611dbcea8b71c4dcaa387276c6c952a7)

![{\displaystyle x_{1}={\sqrt[{5}]{q}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41c80c28b53e727c880b057dcd250e567e4688e8)
![{\displaystyle x_{2}={\sqrt[{5}]{q+p{\sqrt[{5}]{q}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f85db048d997c69b48a38edee7ab7b21ec46d950)
![{\displaystyle x_{n+1}={\sqrt[{5}]{q+px_{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0cbe9e05044219d3b14023ba4850bbf3e07bd3c7)


![{\displaystyle x={\sqrt[{5}]{q+px}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07d9b3f75d07c80a93cea3c6bbd4c19cfd7fd4de)













![{\displaystyle f(\zeta )=f(e^{2\pi i})+\sum _{n=1}^{\infty }{\frac {t^{n}}{n!}}{\frac {d^{n-1}}{da^{n-1}}}[f'(a)|\phi (a)|^{n}]_{a=e^{2\pi i}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5470b684e7bc36a39b1b88cc23f8b5ed2f88dd34)







![{\displaystyle {}_{x_{N}=-{\frac {a}{2b}}{\sqrt {\left({\frac {c}{b}}\right)^{N-1}}}{}_{N-1}F_{N-2}{\begin{bmatrix}{\frac {N+1}{2N}},{\frac {N+3}{2N}},\cdots ,{\frac {N-2}{N}},{\frac {N-1}{N}},{\frac {N+1}{N}},{\frac {N+2}{N}},\cdots ,{\frac {3N-3}{2N}},{\frac {3N-1}{2N}};\\[8pt]{\frac {N+1}{2N-4}},{\frac {N+3}{2N-4}},\cdots ,{\frac {N-4}{N-2}},{\frac {N-3}{N-2}},{\frac {N-1}{N-2}},{\frac {N}{N-2}},\cdots ,{\frac {3N-5}{2N-4}},{\frac {3}{2}};\\[8pt]-{\frac {a^{2}c^{N-2}}{4b^{N}\left(N-2\right)^{N-2}}}\end{bmatrix}}+{\sqrt {\frac {c}{b}}}{\rm {i}}{}_{N-1}F_{N-2}{\begin{bmatrix}{\frac {1}{2N}},{\frac {3}{2N}},\cdots ,{\frac {N-4}{2N}},{\frac {N-2}{2N}},{\frac {N+2}{2N}},{\frac {N+4}{2N}},\cdots ,{\frac {2N-3}{2N}},{\frac {2N-1}{2N}};\\[8pt]{\frac {3}{2N-4}},{\frac {5}{2N-4}},\cdots ,{\frac {2N-3}{2N-4}};\\[8pt]-{\frac {a^{2}c^{N-2}}{4b^{N}\left(N-2\right)^{N-2}}}\end{bmatrix}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d97e039d9837aafc9f8e89800e43e17c8f307a9)
![{\displaystyle {}_{x_{N-1}=-{\frac {a}{2b}}{\sqrt {\left({\frac {c}{b}}\right)^{N-1}}}{}_{N-1}F_{N-2}{\begin{bmatrix}{\frac {N+1}{2N}},{\frac {N+3}{2N}},\cdots ,{\frac {N-2}{N}},{\frac {N-1}{N}},{\frac {N+1}{N}},{\frac {N+2}{N}},\cdots ,{\frac {3N-3}{2N}},{\frac {3N-1}{2N}};\\[8pt]{\frac {N+1}{2N-4}},{\frac {N+3}{2N-4}},\cdots ,{\frac {N-4}{N-2}},{\frac {N-3}{N-2}},{\frac {N-1}{N-2}},{\frac {N}{N-2}},\cdots ,{\frac {3N-5}{2N-4}},{\frac {3}{2}};\\[8pt]-{\frac {a^{2}c^{N-2}}{4b^{N}\left(N-2\right)^{N-2}}}\end{bmatrix}}-{\sqrt {\frac {c}{b}}}{\rm {i}}{}_{N-1}F_{N-2}{\begin{bmatrix}{\frac {1}{2N}},{\frac {3}{2N}},\cdots ,{\frac {N-4}{2N}},{\frac {N-2}{2N}},{\frac {N+2}{2N}},{\frac {N+4}{2N}},\cdots ,{\frac {2N-3}{2N}},{\frac {2N-1}{2N}};\\[8pt]{\frac {3}{2N-4}},{\frac {5}{2N-4}},\cdots ,{\frac {2N-3}{2N-4}};\\[8pt]-{\frac {a^{2}c^{N-2}}{4b^{N}\left(N-2\right)^{N-2}}}\end{bmatrix}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc089fd3ce8f73265814663ae1a92ad84934ccec)
![{\displaystyle {}_{x_{n}=-e^{\frac {2n\pi {\rm {i}}}{N-2}}{\sqrt[{N-2}]{\frac {b}{a}}}{}_{N-1}F_{N-2}{\begin{bmatrix}-{\frac {1}{N\left(N-2\right)}},-{\frac {1}{N\left(N-2\right)}}+{\frac {1}{N}},-{\frac {1}{N\left(N-2\right)}}+{\frac {2}{N}},\cdots ,-{\frac {1}{N\left(N-2\right)}}+{\frac {1}{N}},{\frac {N-5}{2N}},-{\frac {1}{N\left(N-2\right)}}+{\frac {N-3}{2N}},-{\frac {1}{N\left(N-2\right)}}+{\frac {N+1}{2N}},-{\frac {1}{N\left(N-2\right)}}+{\frac {N+3}{2N}},\cdots ,-{\frac {1}{N\left(N-2\right)}}+{\frac {N-1}{N}},;\\[8pt]{\frac {1}{N-2}},{\frac {2}{N-2}},\cdots ,{\frac {2N-5}{2N-4}},;\\[8pt]-{\frac {a^{2}c^{N-2}}{4b^{N}\left(N-2\right)^{N-2}}}\end{bmatrix}}+{\sqrt[{N-2}]{\frac {b}{a}}}\sum _{q=1}^{N-3}{\frac {\Gamma \left({\frac {2q-1}{N-2}}+q\right)}{\Gamma \left({\frac {2q-1}{N-2}}+1\right)}}\cdot \left(-{\frac {c}{b}}{\sqrt[{N-2}]{\frac {a^{2}}{b^{2}}}}\right)^{q}\cdot {\frac {e^{{\frac {2n\left(1-2q\right)}{N-2}}\pi {\rm {i}}}}{q!}}{}_{N-1}F_{N-2}{\begin{bmatrix}{\frac {Nq-1}{N\left(N-2\right)}},{\frac {Nq-1}{N\left(N-2\right)}}+{\frac {1}{N}},{\frac {Nq-1}{N\left(N-2\right)}}+{\frac {2}{N}},\cdots ,{\frac {Nq-1}{N\left(N-2\right)}}+{\frac {N-3}{2N}},{\frac {Nq-1}{N\left(N-2\right)}}+{\frac {N+1}{2N}},\cdots ,{\frac {Nq-1}{N\left(N-2\right)}}+{\frac {N-1}{N}};\\[8pt]{\frac {q+1}{N-2}},{\frac {q+2}{N-2}},\cdots ,{\frac {N-4}{N-2}},{\frac {N-3}{N-2}},{\frac {N-1}{N-2}},{\frac {N}{N-2}},\cdots ,{\frac {q+N-2}{N-2}},{\frac {2q+2N-5}{2N-4}};\\[8pt]-{\frac {a^{2}c^{N-2}}{4b^{N}\left(N-2\right)^{N-2}}}\end{bmatrix}},n=1,2,\cdots ,N-2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/268d3bd45607c3786d1feb5a30ecbbbfc86993ee)


![{\displaystyle f[\phi (a)]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57c239902d7a8ce8bdb1105a18c63c89168db007)
![{\displaystyle {\begin{aligned}{\frac {df[\phi (a)]}{da}}=0\\[6pt]{\frac {d^{2}f[\phi (a)]}{da^{2}}}=0\\[6pt]{\frac {d^{3}f[\phi (a)]}{da^{3}}}=0\\[6pt]{\frac {d^{4}f[\phi (a)]}{da^{4}}}=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12525500e92d5ca66edecd5e1039567bcb7b69b5)
