Квадратный корень
 |
Квадра́тный ко́рень из числа (корень 2-й степени) — число , дающее при возведении в квадрат[1]: Равносильное определение: квадратный корень из числа — решение уравнения Операция вычисления значения квадратного корня из числа называется «извлечением квадратного корня» из этого числа.
Наиболее часто под и подразумеваются вещественные числа, но существуют и обобщения для комплексных чисел и других математических объектов, например, матриц и операторов.
У каждого положительного вещественного числа существуют два противоположных по знаку квадратных корня. Например, квадратными корнями из числа 9 являются и у обоих этих чисел квадраты совпадают и равны 9. Это затрудняет работу с корнями. Чтобы обеспечить однозначность, вводится понятие арифметического корня, значение которого при всегда неотрицательно (а на положительных — положительно); арифметический корень из числа обозначается с помощью знака корня (радикала)[2][3]: .
Пример для вещественных чисел: потому что
Если требуется учесть двузначность корня, перед радикалом ставится знак плюс-минус[2]; например, так делается в формуле решения квадратного уравнения :

История[править | править код]
Первые задачи, связанные с извлечением квадратного корня, обнаружены в трудах вавилонских математиков. Среди таких задач[4]:
- Применение теоремы Пифагора для нахождения стороны прямоугольного треугольника по известным двум другим сторонам.
- Нахождение стороны квадрата, площадь которого задана.
- Решение квадратных уравнений.

Вавилонская глиняная табличка YBC 7289 из вавилонской коллекции Йельского университета была создана между 1800 и 1600 годами до н. э. и демонстрирует √2 и √2/2 соответственно в шестидесятиричной системе счисления: 1;24,51,10 и 0;42,25,35 на квадрате, пересечённом двумя диагоналями[5]. (1;24,51,10) по основанию 60 соответствует 1,41421296, что является правильным значением с точностью до 5 десятичных знаков: Вавилонские математики (II тысячелетие до н. э.) разработали для извлечения квадратного корня особый численный метод[6], изложенный ниже. Аналогичные задачи и методы встречаются в древнекитайской «Математике в девяти книгах»[7].
Древние греки сделали важное открытие: — иррациональное число. Детальное исследование, выполненное Теэтетом Афинским (IV век до н. э.), показало, что если корень из натурального числа не извлекается нацело, то его значение иррационально[8].
Средневековые европейские математики (например, Кардано) обозначали квадратный корень[9] символом Rx, сокращение от слова «radix». Современное обозначение впервые употребил немецкий математик Кристоф Рудольф, из школы коссистов (то есть алгебраистов), в 1525 году[10]. Происходит этот символ от стилизованной первой буквы того же слова «radix». Черта над подкоренным выражением вначале отсутствовала; её позже ввёл Декарт («Геометрии», 1637) для иной цели (вместо скобок), и эта черта вскоре слилась со знаком корня.
После появления формулы Кардано (XVI век) началось применение в математике мнимых чисел, понимаемых как квадратные корни из отрицательных чисел[11]. Основы техники работы с комплексными числами разработал в XVI веке Рафаэль Бомбелли, который также предложил оригинальный метод вычисления корней (с помощью цепных дробей). Открытие формулы Муавра (1707) показало, что извлечение корня любой степени из комплексного числа всегда возможно и не приводит к новому типу чисел[12].
Комплексные корни произвольной степени в начале XIX века глубоко исследовал Гаусс, хотя первые результаты принадлежат Эйлеру[13]. Чрезвычайно важным открытием (Галуа) стало доказательство того факта, что не все алгебраические числа (корни многочленов) могут быть получены из натуральных с помощью четырёх действий арифметики и извлечения корней[14].
Квадратные корни из чисел[править | править код]
Рациональные числа[править | править код]
При рациональных уравнение не всегда разрешимо в рациональных числах. Более того, такое уравнение, даже при положительном , разрешимо в рациональных числах тогда и только тогда, когда и числитель и знаменатель числа , представленного в виде несократимой дроби, являются квадратными числами.
Непрерывная дробь для корня из рационального числа всегда является периодической (возможно, с предпериодом), что позволяет, с одной стороны, легко вычислять хорошие рациональные приближения к рациональным числам с помощью линейных рекурсий, а с другой стороны ограничивает точность приближения: , где зависит от [15][16]. Верно и то, что любая периодическая непрерывная дробь является квадратичной иррациональностью.
Примеры разложения корней из натуральных чисел от 2 до 10 в непрерывные дроби:
= [1; 2, 2, ...] = [1; 1, 2, 1, 2, ...] = [2] = [2; 4, 4, ...] = [2; 2, 4, 2, 4, ...] = [2; 1, 1, 1, 4, 1, 1, 1, 4, ...] = [2; 1, 4, 1, 4, ...] = [3] = [3; 6, 6, ...]
Действительные (вещественные) числа[править | править код]
Для любого положительного числа существуют ровно два вещественных корня, которые равны по модулю и противоположны по знаку[17].
Неотрицательный квадратный корень из неотрицательного числа называется арифметическим квадратным корнем и обозначается с использованием знака радикала[3]: .
Основные свойства вещественного квадратного корня (все подкоренные выражения считаются неотрицательными):
- (корень из произведения равен произведению корней из сомножителей);
- (обобщение)
-
- (обобщение)
К комплексным числам, учитывая двузначность корня, все эти свойства неприменимы (см. ниже пример ошибки).
Комплексные числа[править | править код]
Квадратных корней из любого ненулевого комплексного числа всегда ровно два, они противоположны по знаку. Для корней в комплексной области понятие арифметического корня не вводится, знак радикала обычно либо не используется, либо обозначает не функцию корня, а множество всех корней. В последнем случае, во избежание ошибок, знак радикала не должен использоваться в арифметических операциях. Распространённая ошибка:
- (что, конечно, неверно)
Ошибка возникла из-за того, что комплексный квадратный корень является двузначной функцией, и его нельзя использовать в арифметических действиях.
Для извлечения квадратного корня из комплексного числа удобно использовать экспоненциальную форму записи комплексного числа: если
- ,
то (см. Формула Муавра)
- ,
где корень из модуля понимается в смысле арифметического значения, а k может принимать значения k = 0 и k = 1, таким образом, в итоге получаются два различных результата.
Существует и чисто алгебраическое представление для корня из ; оба значения корня имеют вид где:
Здесь sgn — функция «знак». Формула легко проверяется возведением в квадрат[18].
Пример: для квадратного корня из формулы дают два значения:
Квадратный корень как элементарная функция[править | править код]

Квадратный корень является элементарной функцией и частным случаем степенной функции с . Арифметический квадратный корень является гладким при в нуле же он непрерывен справа, но не дифференцируем[19].
Производная функции квадратного корня вычисляется по формуле:
Как функция комплексного переменного корень — двузначная функция, два листа которой соединяются в нуле (см. подробнее Комплексный анализ).
В элементарной геометрии[править | править код]
Квадратные корни тесно связаны с элементарной геометрией: если дан отрезок длины 1, то с помощью циркуля и линейки можно построить те и только те отрезки, длина которых записывается выражениями, содержащими целые числа, знаки четырёх действий арифметики, квадратные корни и ничего сверх того[20].
В информатике[править | править код]
Во многих языках программирования функционального уровня (а также языках разметки типа LaTeX) функция квадратного корня обозначается как sqrt (от англ. square root «квадратный корень»).
Применение[править | править код]
Квадратные корни используются повсеместно в математике и естественных науках, например:
- (численные методы) в формулах для вычисления корней квадратного уравнения, а также корней уравнения третьей и четвёртой степени;
- (геометрия) в определении евклидовой нормы в евклидовом пространстве, а также в таких обобщениях, как гильбертовы пространства;
- (теория вероятностей и статистика) в определении стандартного отклонения случайной величины;
- (физика) в преобразованиях Лоренца специальной теории относительности участвует множитель
- (небесная механика) период обращения планеты вокруг Солнца связан с большой полуосью её орбиты соотношением: (следствие третьего закона Кеплера).
Алгоритмы нахождения квадратного корня[править | править код]
Разложение в ряд Тейлора[править | править код]
- при .
Грубая оценка[править | править код]
Многие алгоритмы вычисления квадратных корней из положительного действительного числа S требуют некоторого начального значения. Если начальное значение слишком далеко от настоящего значения корня, вычисления замедляются. Поэтому полезно иметь грубую оценку, которая может быть очень неточна, но легко вычисляется. Если S ≥ 1, пусть D будет числом цифр S слева от десятичной запятой. Если S < 1, пусть D будет числом нулей, идущих подряд, справа от десятичной запятой, взятое со знаком минус. Тогда грубая оценка выглядит так:
- Если D нечётно, D = 2n + 1, тогда используем
- Если D чётно, D = 2n + 2, тогда используем
Два и шесть используются потому, что и
При работе в двоичной системе (как внутри компьютеров), следует использовать другую оценку (здесь D это число двоичных цифр).
Геометрическое извлечение квадратного корня[править | править код]

Так как треугольники и подобны по признаку подобия треугольников по 2 равным углам, то откуда и
В частности, если , а , то [21].
Итерационный аналитический алгоритм[править | править код]
Данный способ был известен уже в Древнем Вавилоне. Он позволяет найти приближённое значение квадратного корня с любой точностью,
Последовательные приближения рассчитываются по формуле: тогда
Этот метод сходится очень быстро. Например, если для взять начальное приближение то получим:
В заключительном значении верны все приведённые цифры, кроме последней.
Столбиком[править | править код]
Этот способ позволяет найти приближённое значение корня из любого действительного числа с любой наперёд заданной точностью. К недостаткам способа можно отнести увеличивающуюся сложность вычисления с увеличением количества найденных цифр.
Для ручного извлечения корня применяется запись, похожая на деление столбиком. Выписывается число, корень которого ищем. Справа от него будем постепенно получать цифры искомого корня. Пусть извлекается корень из числа N с конечным числом знаков после запятой. Для начала мысленно или метками разобьём число N на группы по две цифры слева и справа от десятичной точки. При необходимости группы дополняются нулями — целая часть дополняется слева, дробная справа. Так, 31234,567 можно представить как 03 12 34, 56 70. В отличие от деления, снос производится такими группами по 2 цифры.
- Записать число N (в примере — 69696) на листке.
- Найти , квадрат которого меньше или равен группе старших разрядов числа N (старшая группа — самая левая, не равная нулю), а квадрат больше группы старших разрядов числа. Записать найденное справа от N (это очередная цифра искомого корня). (На первом шаге примера , а ).
- Записать квадрат под старшей группой разрядов. Провести вычитание из старшей группы разрядов N выписанного квадрата числа и записать результат вычитания под ними.
- Слева от этого результата вычитания провести вертикальную черту и слева от черты записать число, равное уже найденным цифрам результата (мы их выписываем справа от N), умноженное на 20. Назовём это число . (На первом шаге примера это число просто есть , на втором ).
- Произвести снос следующей группы цифр, то есть дописать следующие две цифры числа N справа от результата вычитания. Назовем число, полученное соединением результата вычитания и очередной группы из двух цифр. (На первом шаге примера это число , на втором ). Если сносится первая группа после десятичной точки числа N, то нужно поставить точку справа от уже найденных цифр искомого корня.
- Теперь нужно найти такое , что меньше или равно , но больше, чем . Записать найденное справа от N как очередную цифру искомого корня. Вполне возможно, что окажется равным нулю. Это ничего не меняет — записываем 0 справа от уже найденных цифр корня. (На первом шаге примера это число 6, так как , но ) Если число найденных цифр уже удовлетворяет искомой точности, прекращаем процесс вычисления.
- Записать число под . Провести вычитание столбиком числа из и записать результат вычитания под ними. Перейти к шагу 4.
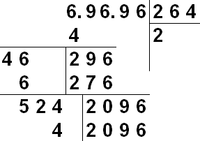
Наглядное описание алгоритма:
Вариации и обобщения[править | править код]
Квадратный корень из определяется как решение уравнения и его в принципе можно определить не только для чисел, но и всюду, где такое уравнение имеет смысл. В общей алгебре применяется следующее формальное определение:
|
Пусть — группоид и . Элемент называется квадратным корнем из если . |
Чаще всего рассматривают такие обобщения в алгебраических кольцах.
Если кольцо есть область целостности, то квадратных корней из ненулевого элемента может быть либо два, либо ни одного. В самом деле, если имеются два корня то откуда: , то есть, в силу отсутствия делителей нуля, . В более общем случае, когда в кольце имеются делители нуля или оно некоммутативно, число корней может быть любым.
В теории чисел рассматривается конечное кольцо вычетов по модулю : если сравнение имеет решение, то целое число называется квадратичным вычетом (в противном случае — квадратичным невычетом). Решение указанного сравнения вполне аналогично извлечению квадратного корня в кольце вычетов[22].
Корни для кватернионов имеют много общего с комплексными, но есть и существенные особенности. Квадратный кватернионный корень обычно имеет 2 значения, но если подкоренное выражение — отрицательное вещественное число, то значений бесконечно много. Например, квадратные корни из образуют трёхмерную сферу, определяемую формулой[23]:
Для кольца квадратных матриц доказано, что если матрица положительно определена, то положительно определённый квадратный корень из матрицы существует и единственен[24]. Для матриц других типов корней может быть сколько угодно (в том числе ни одного).
Квадратные корни вводятся также для функций[25], операторов[26] и других математических объектов.
См. также[править | править код]
Примечания[править | править код]
- ↑ Математическая энциклопедия (в 5 томах), 1982.
- ↑ 1 2 Элементарная математика, 1976, с. 49.
- ↑ 1 2 Корн Г., Корн Т. Справочник по математике, 1970, с. 33.
- ↑ История математики, 1970—1972, Том I, С. 42—46.
- ↑ Analysis of YBC 7289 (англ.). ubc.ca. Дата обращения: 19 января 2015. Архивировано 12 марта 2020 года.
- ↑ История математики, 1970—1972, Том I, С. 47.
- ↑ История математики, 1970—1972, Том I, С. 169—171.
- ↑ Башмакова И. Г. Становление алгебры (из истории математических идей). — М.: Знание, 1979. — С. 23. — (Новое в жизни, науке, технике. Математика, кибернетика, № 9).
- ↑ Никифоровский В. А. Из истории алгебры XVI-XVII вв. — М.: Наука, 1979. — С. 81. — 208 с. — (История науки и техники).
- ↑ Знаки математические // Математическая энциклопедия. — М.: Советская Энциклопедия, 1982. — Т. 2. Архивировано 20 ноября 2012 года.
- ↑ История математики, 1970—1972, Том I, С. 296—298.
- ↑ История математики, 1970—1972, Том III, С. 56—59.
- ↑ История математики, 1970—1972, Том III, С. 62.
- ↑ Колмогоров А. Н., Юшкевич А. П. (ред.). Математика XIX века. Математическая логика, алгебра, теория чисел, теория вероятностей. — М.: Наука, 1978. — Т. I. — С. 58—66.
- ↑ Теорема Лиувилля о приближении алгебраических чисел
- ↑ Хинчин, 1960.
- ↑ Фихтенгольц, 4.
- ↑ Cooke, 2008.
- ↑ Фихтенгольц, 2.
- ↑ Курант, Роббинс, 2000.
- ↑ Курант, Роббинс, 2000, с. 148.
- ↑ Виноградов И. М. Основы теории чисел. — М.—Л.: ГИТТЛ, 1952. — С. 71. — 180 с. Архивировано 4 ноября 2011 года.
- ↑ Porteous, Ian R. Clifford Algebras and the Classical Groups. Cambridge, 1995, page 60.
- ↑ См., например: Гантмахер Ф. Р. Теория матриц. М.: ГИТТЛ, 1953, С. 212—219, или: Воеводин В., Воеводин В. Энциклопедия линейной алгебры. Электронная система ЛИНЕАЛ. Спб.: БХВ-Петербург, 2006.
- ↑ См., например: Ершов Л. В., Райхмист Р. Б. Построение графиков функций. М.: Просвещение, 1984, или: * Каплан И. А. Практические занятия по высшей математике. — Харьков: Изд-во ХГУ, 1966.
- ↑ См., например: Хатсон В., Пим Дж. Приложения функционального анализа и теории операторов. М.: Мир, 1983, или: Халмош П. Гильбертово пространство в задачах. М.: Мир, 1970.
Литература[править | править код]
- Воеводин В. В. Энциклопедия линейной алгебры. Электронная система ЛИНЕАЛ. — Санкт-Петербург: БХВ-Петербург, 2006.
- Ершов Л. В., Райхмист Р. Б. Построение графиков функций. — Москва: Просвещение, 1984.
- Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье. — М.: Наука, 1976. — 591 с.
- История математики, в трёх томах / Под редакцией А. П. Юшкевича. — М.: Наука, 1970—1972.
- Корень // Математическая энциклопедия (в 5 томах). — Москва: Советская Энциклопедия, 1982. — Т. 3.
- Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — 2-е изд.. — Москва: Наука, 1970. — 720 с.
- Курант Р., Роббинс Г. ГЛАВА III Геометрические построения. Алгебра числовых полей // Что такое математика?. — Москва: МЦНМО, 2000.
- Понятов А. Откуда вырос арифметический корень? // Наука и жизнь. — 2022. — № 8. — С. 81—89.
- Фихтенгольц Г. М. Введение, § 4 // [Мат. анализ на EqWorld Курс дифференциального и интегрального исчисления]. — Т. 1.
- Фихтенгольц Г. М. Глава 2, § 1 // [Мат. анализ на EqWorld Курс дифференциального и интегрального исчисления]. — Т. 1.
- Халмош П. Гильбертово пространство в задачах. — Москва: Мир, 1970.
- Хатсон В., Пим Дж. Приложения функционального анализа и теории операторов. — Москва: Мир, 1983.
- Хинчин А. Я. §§ 4, 10 // Цепные дроби. — Москва: ГИФМЛ, 1960.
- Cooke, Roger. Classical algebra: its nature, origins, and uses (англ.). — John Wiley and Sons, 2008. — P. 59. — ISBN 0-470-25952-3.
Ссылки[править | править код]
- Алгоритмы вычисления квадратного корня (англ.). Дата обращения: 12 октября 2006. Архивировано 19 ноября 2010 года.
- Соловьев Ю. Старый алгоритм. Дата обращения: 6 ноября 2006. Архивировано 3 марта 2016 года.






















































![{\displaystyle {\sqrt {\sqrt {1\cdot 10}}}={\sqrt[{4}]{10}}\approx 2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2eeb6a3f3bd5de4533a82fdb3dfd8d86223ffc1)
![{\displaystyle {\sqrt {\sqrt {10\cdot 100}}}={\sqrt[{4}]{1000}}\approx 6\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95b0b8d8cc44d57a544d6398144d88707458ffa0)