Гамма-функция

Гамма-функция — математическая функция, которая расширяет понятие факториала на поле комплексных чисел. Обычно обозначается $\Gamma (z)$.

Была введена Леонардом Эйлером, а своим обозначением гамма-функция обязана Лежандру.

Определение

График гамма-функции действительного переменного

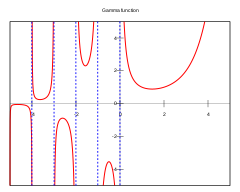
Если вещественная часть комплексного числа $z$ положительна, то Гамма-функция определяется через интеграл

$~\Gamma (z)=\int \limits _{0}^{+\infty }\!t^{\,{\mathrm {z} }-1}e^{-t}\,dt$

На всю комплексную плоскость функция распространяется через тождество

$~\Gamma (z+1)=z\Gamma (z)$.

Альтернативное определение

Следующее бесконечное произведение служит альтернативным определением Гамма-функции. Оно верно для всех комплексных $z$, за исключением 0 и отрицательных целых

$\Gamma (z)=\lim _{n\to \infty }{\frac {n!\;n^{\mathrm {z} }}{z\;(z+1)\cdots (z+n)}}={\frac {1}{z}}\prod _{n=1}^{\infty }{\frac {\left(1+{\frac {1}{n}}\right)^{\mathrm {z} }}{1+{\frac {\mathrm {z} }{n}}}}$

Замечания

• Интеграл выше сходится абсолютно если вещественная часть комплексного числа $z$ положительна.
• Применяя интегрирование по частям, можно показать, что тождество

  $\Gamma (z+1)=z\Gamma (z)$

выполняется для подынтегрального выражения.

• А поскольку $\Gamma (1)=1$, для всех натуральных чисел $n$

$\Gamma (n+1)=n\cdot \Gamma (n)=\ldots =n!\cdot \Gamma (1)=n!$

• $\Gamma (z)$ является мероморфной на комплексной плоскости и имеющей полюса в точках $z=0,\;-1,\;-2,\;-3,\;\ldots$

Связанные определения

• Иногда используется альтернативная запись, так называемая пи-функция, зависящая от гамма-функции следующим образом:

  $\Pi (z)=\Gamma (z+1)=z\Gamma (z)$.

• В интеграле выше, определяющем гамма-функцию, пределы интегрирования фиксированы. В неполной гамма-функции допускается, чтобы верхний либо нижний предел интегрирования был переменным. Неполную гамма-функцию часто обозначают как гамма-функцию от двух аргументов:

  $\Gamma (a,z)=\int \limits _{\mathrm {z} }^{\infty }\!{e^{-t}t^{a-1}\,dt}$.

Свойства

График модуля гамма-функции на комплексной плоскости.

• формула дополнения

  $\Gamma (1-z)\Gamma (z)={\pi \over \sin \pi z}$.

• Вероятно, наиболее известное значение гамма-функции от нецелого аргумента это

  $\Gamma \left({\frac {1}{2}}\right)={\sqrt {\pi }}$.

• Гамма-функция имеет полюс в $z=-n$ для любого натурального $n$ и нуля; вычет в этой точке задается так

  $\operatorname {\mathrm {Res} } _{z=-n}\,\Gamma (z)={\frac {(-1)^{n}}{n!}}$.

• Следующее бесконечное произведение для гамма-функции, как показал Вейерштрасс, верно для всех комплексных $z$, не являющихся неположительными целыми:

  $\Gamma (z)={\frac {e^{-\gamma z}}{z}}\prod _{k=1}^{\infty }\left(1+{\frac {z}{k}}\right)^{-1}e^{z/k}$,

где $\gamma$ — это константа Эйлера.

• формула, полученная Гауссом:

  $\Gamma (z)\Gamma \left(z+{\frac {1}{n}}\right)\ldots \Gamma \left(z+{\frac {n-1}{n}}\right)=n^{{\frac {1}{2}}-nz}\cdot (2\pi )^{\frac {n-1}{2}}\Gamma (nz)$.

• Основное, но полезное свойство, которое может быть получено из предельного определения:

  ${\overline {\Gamma (z)}}=\Gamma ({\overline {z}})$.

• Гамма-функция дифференцируема бесконечное число раз, и $\Gamma ^{\prime }(x)=\psi (x)\Gamma (x)$, где $\psi (x)$ часто называют «пси-функцией», или дигамма-функцией.
• Гамма-функция и бета-функция связаны следующим соотношением:

  $\mathrm {B} (x,\;y)={\frac {\Gamma (x)\Gamma (y)}{\Gamma (x+y)}}$.

• Гамма-функция является частным случаем преобразования Меллина.

См. также

• Список объектов, названных в честь Леонарда Эйлера
• K-функция
• G-функция
• Бета-функция