Участник:Преподаватель техникума/Задания: различия между версиями

Содержимое удалено Содержимое добавлено

Линейный

Версия от 07:08, 3 сентября 2020

ДИСТАНЦИОННОЕ ЗАДАНИЕ ПО МАТЕМАТИКЕ

Тема: Корень степени n Цель: Узнать о вычислении корней. Дата выдачи: 3 сентября 2020. Дата окончания работы: 10 сентября 2020 года.

Это статья об извлечении корней. См. также Корень уравнения и Корень многочлена.

Корень $n$ -й степени из числа $a$ определяется^[1] как такое число $b$ , что $b^{n}=a.$ Здесь $n$ — натуральное число, называемое показателем корня (или степенью корня); как правило, оно больше или равно 2, потому что случай $n=1$ не представляет интереса.

Обозначение: $b={\sqrt[{n}]{a}},$ символ (знак корня) в правой части называется радикалом. Число $a$ (подкоренное выражение) чаще всего вещественное или комплексное, но существуют и обобщения для других математических объектов, например, вычетов, матриц и операторов, см. ниже #Вариации и обобщения.

Примеры для вещественных чисел:

Корнями 2-й степени из числа 9 являются $+3$ и $-3,$ у обоих этих чисел квадраты совпадают и равны 9
${\sqrt[{3}]{\ 64}}=4,$ потому что $4^{3}=64.$
${\sqrt[{3}]{\frac {8}{27}}}={\frac {2}{3}},$ потому что $\left({\frac {2}{3}}\right)^{3}={\frac {8}{27}}.$

Как видно из первого примера, у вещественного корня чётной степени могут быть два значения (положительное и отрицательное), и это затрудняет работу с такими корнями, не позволяя использовать их в арифметических вычислениях. Чтобы обеспечить однозначность, вводится понятие арифметического корня^[⇨] (из неотрицательного вещественного числа), значение которого всегда неотрицательно, в первом примере это число $3.$ Кроме того, принято соглашение, по которому знак корня чётной степени из вещественного числа всегда обозначает арифметический корень^[2]^[3]: ${\sqrt[{2}]{9}}=3.$ Если требуется учесть двузначность корня, перед радикалом ставится знак плюс-минус^[2]; например, так делается в формуле решения квадратного уравнения $ax^{2}+bx+c=0$ :

x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}

Вещественные корни чётной степени из отрицательных чисел не существуют. Из комплексного числа всегда можно извлечь корень любой степени, но результат определён неоднозначно — комплексный корень $n$ -й степени из ненулевого числа имеет $n$ различных значений (см. #Корни из комплексных чисел).

Операция извлечения корня и алгоритмы её реализации появились в глубокой древности в связи с практическими потребностями геометрии и астрономии, см. #История.

Определение и связанные понятия

Кроме приведенного выше, можно дать два равносильных определения корня^[4]:

Корень $n$ -й степени из числа $a$ есть решение $x$ уравнения $x^{n}=a$ (отметим, что решений может быть несколько или ни одного)
Корень $n$ -й степени из числа $a$ есть корень многочлена $x^{n}-a,$ то есть значение $x$ , при котором указанный многочлен равен нулю.

Операция вычисления ${\sqrt[{n}]{a}}$ называется «извлечением корня $n$ -й степени» из числа $a$ . Это одна из двух операций, обратных по отношению к возведению в степень^[5], а именно — нахождение основания степени $b$ по известному показателю $n$ и результату возведения в степень $a=b^{n}$ . Вторая обратная операция, логарифмирование, находит показатель степени по известным основанию и результату.

Корни второй и третьей степени употребляются особенно часто и поэтому имеют специальные названия^[5].

Квадратный корень: ${\sqrt {a}}.$ В этом случае показатель степени 2 обычно опускается, а термин «корень» без указания степени чаще всего подразумевает квадратный корень. Геометрически ${\sqrt {a}}$ можно истолковать как длину стороны квадрата, площадь которого равна $a$ .
Кубический корень: ${\sqrt[{3}]{a}}.$ Геометрически ${\sqrt[{3}]{a}}$ — это длина ребра куба, объём которого равен $a$ .

Корни из вещественных чисел

В данном разделе всюду $n$ — натуральное число, $a,b$ — вещественные числа. Корень $n$ -й степени из вещественного числа $a$ , в зависимости от чётности $n$ и знака $a$ , может иметь от 0 до 2 вещественных значений.

Общие свойства

Корень нечётной степени из положительного числа — положительное число, однозначно определенное.

${\sqrt[{n}]{a}}=b$ , где $a,b>0,$ $n$ — нечётное

Например,

{\sqrt[{3}]{125}}=5,\ {\sqrt[{5}]{32}}=2,\ {\sqrt[{15}]{1}}=1

Корень нечётной степени из отрицательного числа — отрицательное число, однозначно определенное.

${\sqrt[{n}]{a}}=b$ , где $a,b<0,$ $n$ — нечётное

Например,

{\sqrt[{3}]{-8}}=-2,\ {\sqrt[{5}]{-243}}=-3,\ {\sqrt[{7}]{-1}}=-1

Корень чётной степени из положительного числа имеет два значения с противоположными знаками, но равными по модулю.

$\pm {\sqrt[{n}]{a}}=\pm b$ , где $a,b>0,$ $n$ — чётное

Например,

\pm {\sqrt {4}}=\pm 2,\ \ \pm {\sqrt[{4}]{81}}=\pm 3,\ \ \pm {\sqrt[{10}]{1024}}=\pm 2

Корень чётной степени из отрицательного числа не существует в области вещественных чисел, поскольку при возведении любого вещественного числа в степень с чётным показателем результатом будет неотрицательное число. Ниже будет показано, как извлекать такие корни в более широкой системе — множестве комплексных чисел (тогда значениями корня будут $n$ комплексных чисел).

${\sqrt[{n}]{a}}$ не существует в области вещественных чисел, если $a<0,$ $n$ — чётное

Корень любой натуральной степени из нуля — ноль.

${\sqrt[{n}]{0}}=0$

Предостережение

Как сказано выше: «Корень чётной степени из отрицательного числа не существует в области вещественных чисел». При этом в области комплексных чисел такой корень существует. Поэтому следует всегда учитывать, в какой числовой системе (вещественных или комплексных чисел) мы извлекаем корень.

Пример. В области вещественных чисел, квадратный корень из $-9$ не существует.
Пример. В области комплексных чисел, квадратный корень из $-9$ равен $\pm 3i.$

Арифметический корень

Выше уже говорилось, что корни чётной степени определены, вообще говоря, неоднозначно, и этот факт создаёт неудобства при их использовании. Поэтому было введено практически важное ограничение этого понятия^[6].

Арифметический корень $n$ -й степени из неотрицательного вещественного числа $a$ — это неотрицательное число $b$ , для которого $b^{n}=a.$ Обозначается арифметический корень знаком радикала.

Таким образом, арифметический корень, в отличие от корня общего вида (алгебраического, определяется только для неотрицательных вещественных чисел, а его значение всегда существует, однозначно^[7] и неотрицательно. Например, квадратный корень из числа $4$ имеет два значения: $2$ и $-2$ , из них арифметическим является первое.

Алгебраические свойства

Приведённые ниже формулы верны, прежде всего, для арифметических корней любой степени (кроме особо оговоренных случаев). Они справедливы также для корней нечётной степени, у которых допускаются и отрицательные подкоренные выражения^[8].

Взаимопогашение корня и степени:^[9]
- для нечётного $n$ : ${\sqrt[{n}]{a^{n}}}=a$ ,
- для чётного $n$ : ${\color {blue}{\sqrt[{\color {black}n}]{\color {black}{a^{n}}}}}=|a|$
Если $a<b$ , то и ${\color {blue}{\sqrt[{\color {black}n}]{\color {black}{a}}}}<{\color {blue}{\sqrt[{\color {black}n}]{\color {black}{b}}}}$

Корень из произведения равен произведению корней из сомножителей:

${\color {blue}{\sqrt[{\color {black}n}]{\color {black}{ab}}}}={\color {blue}{\sqrt[{\color {black}n}]{\color {black}{a}}}}{\color {blue}{\sqrt[{\color {black}n}]{\color {black}{b}}}}$

Аналогично для деления:

${\color {blue}{\sqrt[{\color {black}n}]{\color {black}{\frac {a}{b}}}}}={\frac {\color {blue}{\sqrt[{\color {black}n}]{\color {black}{a}}}}{\color {blue}{\sqrt[{\color {black}n}]{\color {black}{b}}}}},\;b\neq 0$

Следующее равенство есть определение возведения в дробную степень^[10]:

$a^{m/n}={\color {blue}{\sqrt[{\color {black}n}]{\color {black}{a^{m}}}}}=\left({\color {blue}{\sqrt[{\color {black}n}]{\color {black}{a}}}}\right)^{m}=\left(a^{1/n}\right)^{m}$

Величина корня не изменится, если его показатель и степень подкоренного выражения разделить на одно и то же число (множитель показателя степени и показатель степени подкоренного выражения):

${\color {blue}{\sqrt[{\color {black}nk}]{\color {black}{a^{mk}}}}}={\color {blue}{\sqrt[{\color {black}n}]{\color {black}{a^{m}}}}},\;n,k\in \mathbb {N} .$ Пример: ${\color {blue}{\sqrt[{\color {black}6}]{\color {black}{64}}}}={\color {blue}{\sqrt[{\color {black}{2\cdot 3}}]{\color {black}{4^{3}}}}}={\color {blue}{\sqrt {\color {black}{4}}}}=2$
${\color {blue}{\sqrt[{\color {black}n}]{\color {blue}{\sqrt[{\color {black}k}]{\color {black}{a}}}}}}={\color {blue}{\sqrt[{\color {black}nk}]{\color {black}{a}}}},\;n,k\in \mathbb {N}$

Для корней нечётной степени укажем дополнительное свойство:

${\sqrt[{n}]{-a}}=-{\sqrt[{n}]{a}}$

Извлечение корня и возведение в дробную степень

Операция возведения в степень первоначально была введена как сокращённая запись операции умножения натуральных чисел: $m^{n}={\color {Gray}\underbrace {\color {Black}m\cdot m\cdot \dots \cdot m} _{\color {Black}n}}$ . Следующим шагом было определение возведения в произвольную целую, в том числе отрицательную, степень: $m^{-n}={\frac {1}{m^{n}}}.$

Операция извлечения арифметического корня позволяет определить возведение положительного числа в любую рациональную (дробную) степень^[10]:

a^{\frac {m}{n}}={\color {blue}{\sqrt[{\color {black}n}]{\color {black}{a^{m}}}}},

a>0

При этом числитель $m$ дроби ${\frac {m}{n}}$ может иметь знак. Свойства расширенной операции в основном аналогичны возведению в целую степень.

Это определение означает, что извлечение корня и обратное к нему возведение в степень фактически объединяются в одну алгебраическую операцию. В частности:

{\color {blue}{\sqrt[{\color {black}n}]{\color {black}{a}}}}=a^{\frac {1}{n}}

Попытки возведения в рациональную степень отрицательных чисел могут привести к ошибкам, поскольку значение алгебраического корня неоднозначно, а область значений арифметического корня ограничена неотрицательными числами. Пример возможной ошибки:

-1=(-1)^{2\ \cdot \ {\frac {1}{2}}}=\left({(-1)^{2}}\right)^{\frac {1}{2}}=1^{\frac {1}{2}}={\color {blue}{\sqrt {\color {black}1}}}=1

Функция корня

Графики функций корня
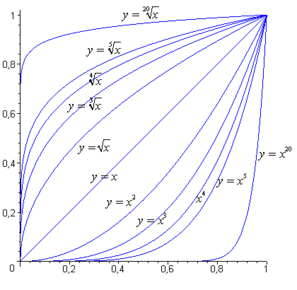
Функции корня и обратные к ним степенные функции на интервале $[0;\ 1]$
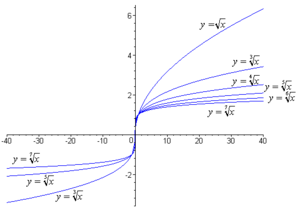
Функции корня:
— арифметический, чётные степени 2, 4, 6
— общий, нечётные степени 3, 5, 7

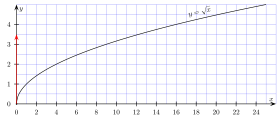
Если рассматривать подкоренное выражение как переменную, мы получим функцию корня $n$ -й степени: $y={\sqrt[{n}]{x}}$ . Функция корня относится к категории алгебраических функций. График любой функции корня проходит через начало координат и точку $(1;\ 1)$ .

Как сказано выше, для корня чётной степени, чтобы обеспечить однозначность функции, корень должен быть арифметическим, так что аргумент $x$ неотрицателен. Функция корня нечётной степени однозначна и существует для любого вещественного значения аргумента.

Тип функции корня	Область определения	Область значений	Другие свойства
Чётной степени	$[0;\ +\infty )$	$[0;\ +\infty )$	Функция выпукла вверх на всей области определения
Нечётной степени	$(-\infty ;+\infty )$	$(-\infty ;+\infty )$	Функция нечётна

Видеоуроки

↑ Корень // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
↑ ¹ ² Элементарная математика, 1976, с. 49.
↑ Корн Г., Корн Т. Справочник по математике, 1970, с. 33.
↑ Сканави М. И. Элементарная математика. П. 1.11. С. 49.
↑ ¹ ² Выгодский М. Я. Справочник по элементарной математике, 1978, с. 64.
↑ Арифметический корень // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 1.
↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Т. I, С. 35—36.
↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 141—143.
↑ Алгебра и начала анализа. Учебник для 10—11 классов, под ред. А. Н. Колмогорова. М.: Просвещение, 2002, С. 209.
↑ ¹ ² Выгодский М. Я. Справочник по элементарной математике, 1978, с. 183.

[1] Корень // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.

[ZAY49-2] ¹ ² Элементарная математика, 1976, с. 49.

[KORN33-3] Корн Г., Корн Т. Справочник по математике, 1970, с. 33.

[4] Сканави М. И. Элементарная математика. П. 1.11. С. 49.

[VYG64-5] ¹ ² Выгодский М. Я. Справочник по элементарной математике, 1978, с. 64.

[6] Арифметический корень // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 1.

[_69c373c8f2c3669c-7] Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Т. I, С. 35—36.

[VYG141-8] Выгодский М. Я. Справочник по элементарной математике, 1978, с. 141—143.

[9] Алгебра и начала анализа. Учебник для 10—11 классов, под ред. А. Н. Колмогорова. М.: Просвещение, 2002, С. 209.

[VYG183-10] ¹ ² Выгодский М. Я. Справочник по элементарной математике, 1978, с. 183.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

Участник:Преподаватель техникума/Задания: различия между версиями

Версия от 07:08, 3 сентября 2020

Содержание

Определение и связанные понятия