Гигантское магнетосопротивление
Гига́нтское магнетосопротивле́ние, гигантское магнитосопротивление[1], ГМС (англ. Giant magnetoresistance, GMR) — квантовомеханический эффект, наблюдаемый в тонких металлических плёнках, состоящих из чередующихся ферромагнитных и проводящих немагнитных слоёв. Эффект состоит в существенном изменении электрического сопротивления такой структуры при изменении взаимного направления намагниченности соседних магнитных слоёв. Направлением намагниченности можно управлять, например, приложением внешнего магнитного поля. В основе эффекта лежит рассеяние электронов, зависящее от направления спина. За открытие гигантского магнетосопротивления в 1988 году физики Альбер Ферт (Университет Париж-юг XI) и Петер Грюнберг (Исследовательский центр Юлих) были удостоены Нобелевской премии по физике в 2007 году.
Основная сфера применения эффекта — датчики магнитного поля, используемые для считывания информации в жёстких дисках, биосенсорах, устройствах МЭМС и др. Обладающие гигантским магнетосопротивлением многослойные структуры применялись в магниторезистивной оперативной памяти в качестве ячеек, хранящих один бит информации.
В литературе термин гигантское магнетосопротивление иногда путается с колоссальным магнетосопротивлением (КМС) ферро- и антиферромагнитных полупроводников[2][3], не связанным с многослойной структурой.
Математическая формулировка[править | править код]
Магнетосопротивлением называют зависимость электрического сопротивления образца от величины внешнего магнитного поля. Численно его характеризуют величиной
где — сопротивление образца в отсутствие магнитного поля, а — его сопротивление в магнитном поле с напряжённостью [4][5]. На практике также применяются альтернативные формы записи, отличающиеся знаком выражения и использующие удельное электрическое сопротивление[1][2]. Иногда используют отношение изменения сопротивления к его значению в нулевом поле[6].
Термин «гигантское магнетосопротивление» указывает на то, что величина для многослойных структур значительно превосходит анизотропное магнитное сопротивление, как правило, составляющее не более нескольких процентов[7][8].
История открытия[править | править код]

Эффект ГМС был экспериментально открыт в 1988 году двумя научными коллективами независимо друг от друга: лабораториями Альбера Ферта и Петера Грюнберга. Практическая значимость этого открытия была отмечена присуждением Ферту и Грюнбергу Нобелевской премии по физике в 2007 году[9].
Предыстория[править | править код]
Первые математические модели, описывающие влияние намагниченности материалов на подвижность носителей тока в них благодаря наличию спина, появились ещё в 1936 году. Экспериментальные факты, свидетельствующие о потенциальной возможности усиления эффекта зависимости сопротивления от магнитного поля (то есть увеличения ), были известны с 1960-х годов. К концу 1980-х годов физиками было хорошо изучено анизотропное магнитное сопротивление[10][11], но величина для этого эффекта не превышала нескольких процентов[7]. Практическое исследование методов увеличения стало возможным с появлением методов наподобие молекулярно-лучевой эпитаксии, позволяющих изготовлять тонкие многослойные плёнки толщиной в единицы нанометров[12].
Эксперимент и его объяснение[править | править код]
Ферт и Грюнберг изучали эффекты, связанные с электрическим сопротивлением структур, включающих в себя ферромагнитные и неферромагнитные материалы. В частности, Ферт занимался проводимостью многослойных плёнок, а Грюнберг в 1986 году открыл обменное взаимодействие антиферромагнитного характера в плёнках Fe/Cr[12].
В работе, в которой было заявлено об открытии эффекта, исследовалось магнетосопротивление (001)Fe/(001)Cr сверхрешёток. В этом эксперименте на объёмноцентрированную кубическую решётку (001)GaAs в высоком вакууме наносились слои железа и хрома при температуре подложки около 20 °C[13].
При толщине слоёв железа в 3 нм и варьировании толщины немагнитной прослойки из хрома между ними от 0,9 до 3 нм увеличение толщины прослоек хрома в сверхрешётке ослабляло антиферромагнитную связь между слоями железа и поле размагничивания. Последнее также уменьшалось при увеличении температуры от 4,2 К до комнатной. Изменение толщины немагнитных прослоек приводило к существенному уменьшению остаточной намагниченности в петле гистерезиса. Была показана сильная зависимость сопротивления образца (изменение до 50 %) от величины внешнего магнитного поля при температуре 4,2 К. В статье Ферта 1988 года новый эффект был назван гигантским магнетосопротивлением, чтобы подчеркнуть его значительную величину по сравнением с анизотропным магнетосопротивлением[13][14].
Авторы открытия также высказали предположение, что в основе эффекта лежит так называемое спин-зависимое рассеяние электронов в сверхрешётке (зависимость сопротивления слоёв от взаимной ориентации их намагниченности и направления спинов электронов)[13]. Теоретическое описание ГМС для различных направлений тока было сделано в течение последующих нескольких лет. Направление тока вдоль слоёв (так называемая CIP-геометрия, англ. current in plane — ток в плоскости) в классическом приближении было исследовано Р. Кэмли в 1989 году[15], а в квантовом — П. Леви в 1990 году[16]. Теория ГМС для тока, направленного перпендикулярно слоям (CPP-геометрия, англ. current perpendicular to plane — ток перпендикулярно плоскости), известная как теория Валета — Ферта, была опубликована в 1993 году[17]. В то же время практический интерес представляет CPP-геометрия[18], так как датчики на его основе, впервые предложенные Р. Ротмайером в 1994 году, демонстрируют бо́льшую чувствительность, чем датчики на основе CIP[19].
Теория[править | править код]
Основные положения[править | править код]
Спин-зависимое рассеяние[править | править код]

Электрическое сопротивление образца зависит от многих факторов, среди которых в магнитоупорядоченных материалах существенную роль играет рассеяние электронов на магнитной подрешётке кристалла, то есть совокупности кристаллографически эквивалентных атомов с ненулевым атомным магнитным моментом, образующих собственную кристаллическую решётку. Рассеяние зависит от ориентации спина электрона по отношению к магнитным моментам атомов. Обычно предполагается, что электроны проводимости минимально взаимодействуют с атомами, чей магнитный момент имеет параллельное их спину направление, и максимально, если они антипараллельны. Взаимодействие также будет сильным в парамагнитном состоянии, в котором магнитные моменты атомов направлены хаотически, без выделенного направления намагниченности[1][7][20].
Для таких хороших проводников, как золото или медь, уровень Ферми находится внутри зоны sp, а зона d полностью заполнена. В ферромагнетиках наблюдается иная ситуация. В них зависимость взаимодействия электронов с атомами от направления их спинов связана с заполненностью зоны, отвечающей за магнитные свойства (3d для таких ферромагнитных металлов, как железо, никель или кобальт). d-зона ферромагнетиков является расщеплённой, так как она содержит различное количество электронов со спинами, направленными «вверх» и «вниз». Это является причиной различия в плотности электронных состояний на уровне Ферми для спинов, направленных в противоположные стороны. Тут говорят о неосновном направлении спинов электронов (англ. minority-spin electrons) для той части зоны d, которая заполнена меньше (например, где спины направлены вниз), и основном для второй её части (англ. majority-spin electrons), которая оказывается заполненной полностью (спины направлены вверх). Уровень Ферми для основного направления спина находится внутри зоны sp, и их движение в ферромагнетике подобно движению электронов в немагнитном металле. Для неосновного направления спинов электронов sp- и d-зоны оказываются гибридизированными, а уровень Ферми лежит внутри зоны d. Гибридизированная зона spd ферромагнетиков характеризуется высокой плотностью состояний, что проявляется как уменьшение длины свободного пробега зонами[1][7] электронов с неосновным направлением спина по сравнению с основным. В никеле, легированном кобальтом, отношение (для электронов с противоположными направлениями спина) может увеличиваться до 20 или понижаться до 0,3 при легировании хромом[21].
Согласно теории Друде, проводимость пропорциональна длине свободного пробега[22] и знание позволяет оценить соотношение проводимостей для этих двух групп носителей тока. Типичное значение длины свободного пробега электронов в тонких металлических плёнках лежит в интервале от нескольких единиц до нескольких десятков нанометров. Электрон «помнит» направление спина на так называемой длине спиновой релаксации (ещё называемой длиной спиновой диффузии), которая может значительно превосходить длину свободного пробега. Она определяет эффективность спин-поляризованного транспорта электронов. Когда наблюдается зависимость электрического сопротивления от направления спина носителя тока, говорят о спин-зависимом распространении электронов. Спин-зависимое рассеяние в ферромагнетиках происходит при переходах электронов проводимости между зонами нерасщеплённой 4s и расщеплённой 3d[1][7].
Существуют материалы, для которых более слабым является взаимодействие между электронами и атомами, чьи спины и магнитные моменты антипараллельны. Комбинацией обоих типов материалов можно получить так называемый инверсный эффект ГМС[7][23]. Поэтому в случаях, когда конкретный механизм взаимодействия не принципиален, для сохранения общности подхода говорят о проводимости для электронов с основным и неосновным направлениями спина, которым соответствуют бо́льшая и меньшая плотность электронных состояний. Определение соотношения между проводимостями или удельными сопротивлениями для этих двух групп электронов является достаточным для построения феноменологической теории[24][25].
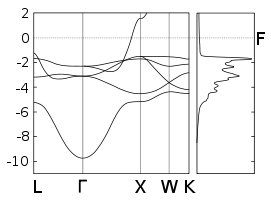
- Электронная зонная структура (слева) и плотность состояний (справа)
-
Кобальт (основное направление спинов)
-
Кобальт (неосновное направление спинов)
CIP и CPP геометрии подключения[править | править код]

Магнитную сверхрешётку можно включить в электрическую цепь двумя способами. При так называемой CIP-геометрии (англ. current in plane, ток в плоскости), электрический ток распространяется вдоль слоёв сверхрешётки, а электроды расположены на одной стороне всей структуры. При геометрии CPP (англ. current perpendicular to plane, ток перпендикулярно плоскости) ток распространяется перпендикулярно слоям сверхрешётки, а электроды расположены по разные её стороны[7]. CPP-геометрия характеризуется бо́льшими величинами ГМС (более чем в два раза по сравнению с CIP), но и представляет бо́льшие сложности для технической реализации[26][27].
Пропускание тока через магнитную сверхрешётку[править | править код]

Характеристики магнитной упорядоченности различны в сверхрешётках с ферромагнитным (ФСР) и антиферромагнитным (АСР) взаимодействием между слоями. В первой направления намагниченности в различных ферромагнитных слоях в отсутствие приложенного поля одинаковы, во второй противоположные направления чередуются. Распространяясь через ФСР, электроны с антипараллельным направлением спина по отношению к намагниченности решётки практически не будут рассеиваться, а электроны со спином, сонаправленным с намагниченностью слоёв, будут испытывать рассеяние. При прохождении АСР рассеиваться будут электроны с любым направлением спинов: акты рассеяния для каждого отдельно выбранного электрона будут иметь место при прохождении слоя с намагниченностью, сонаправленной его спину. Так как величина сопротивления образца возрастает с ростом количества актов рассеяния, сопротивление АСР будет выше, чем ФСР[1][7].
Для построения устройств, использующих эффект ГМС, необходимо иметь возможность динамически переключать состояние решётки между состояниями с параллельной или антипараллельной намагниченностью слоёв. В первом приближении плотность энергии взаимодействия двух ферромагнитных слоёв, разделённых немагнитной прослойкой, пропорциональна скалярному произведению их намагниченностей:
Зависимость коэффициента от толщины немагнитной прослойки описывается осциллирующей функцией. Поэтому может менять и величину, и знак. Если подобрать таким образом, что основным будет антипараллельное состояние, то переключение сверхрешётки из антипараллельного состояния (высокое сопротивление) в параллельное (низкое сопротивление) будет происходить под воздействием внешнего поля. Полное сопротивление структуры можно представить в виде
где — сопротивление ФСР, — инкремент ГМС, — угол между намагниченностями соседних слоёв[26].
Математическое описание[править | править код]
Для математической формализации явления вводятся два так называемых спиновых канала электропроводимости, соответствующих проводимости электронов, для которых сопротивление минимально или максимально соответственно. Соотношение между ними часто определяется в терминах коэффициента спиновой анизотропии , который можно ввести определением минимального и максимального удельных электрических сопротивлений для спин-поляризированного тока в виде
где — среднее удельное сопротивление ферромагнетика[28].
Резисторная модель для структур CIP и CPP[править | править код]
В условиях, когда рассеяние носителей тока на границе между ферромагнитным и немагнитным металлом мало, а направление спинов электронов сохраняется достаточно долго, удобно рассматривать модель, в которой сопротивление образца будет определяться сопротивлениями магнитных и немагнитных слоёв по отдельности.
Наличие двух каналов проводимости для электронов с различным направлением спина по отношению к намагниченности в слоях структуры означает, что эквивалентная схема ГМС-структуры будет состоять из двух параллельных соединений, соответствующих каждому из каналов. В таком случае выражение для магнетосопротивления принимает вид
где индексы у R обозначают сонаправленную и противонаправленную ориентации намагниченности в слоях, — отношение толщин немагнитного и магнитного металлов, — удельное сопротивление немагнитного металла. Данное выражение применимо для CIP- и CPP-структур. При выполнении условия эту зависимость можно переписать в более простом виде через коэффициент спиновой асимметрии:
Подобный прибор, чье сопротивление различно для электронов с различными направлениями спина, принято называть спиновым клапаном. Говорят, что он открыт, если намагниченности в его слоях ориентированы параллельно, и закрыт в противоположном случае[29].
Пусть сверхрешётка состоит из двух магнитных слоёв толщиной a и немагнитной прослойки толщиной b между ними. Если считать, что при прохождении такой структуры время пребывания электрона в каждом из слоёв пропорционально его толщине, то удельное сопротивление структуры может быть записано в виде
где индексы F1 и F2 обозначают первый и второй магнитные слои соответственно, а N — немагнитный слой. Если пренебречь рассеянием электронов при прохождении границ между слоями и спиновой релаксацией, то для образца длиной L и площадью сечения S сопротивления с параллельной и антипараллельной конфигурациями намагниченности будут иметь вид
Тут индексы у интегральных сопротивлений R обозначают сонаправленность намагниченности в слоях структуры (здесь учтено, что эквивалентная схема структуры выглядит как параллельное соединение каналов для электронов с противоположными направлениями спинов). Тогда магнетосопротивление можно записать как
где [30].
Как и для CIP, эквивалентная схема CPP-структуры состоит из параллельно соединённых каналов сопротивлений для электронов с противоположными направлениями спинов. Отличие от предыдущего случая состоит лишь в коэффициенте пропорциональности между удельным и интегральным сопротивлениями, так как электрон теперь должен преодолеть не продольный размер L, а толщины слоёв a и b. Если обозначить через S площадь структуры, то
Это означает, что выражение для магнетосопротивления не изменится:
- [31].
Модель Валета — Ферта[править | править код]
В 1993 году Тьери Валетом (англ. Thierry Valet) и Альбером Фертом была опубликована модель гигантского магнетосопротивления для CPP-геометрии, построенная на основе уравнений Больцмана. Суть теории заключается в рассмотрении расщепления химического потенциала на две функции внутри магнитного слоя, соответствующие электронам со спинами параллельными и антипараллельными намагниченности в нём. Если считать, что толщина немагнитного материала достаточно мала, то во внешнем поле E0 поправки к электрохимическому потенциалу и полю внутри образца будут иметь вид
где ls — средняя длина спиновой релаксации, а координата отсчитывается от границы между магнитным и немагнитным слоями ( соответствует ферромагнетик)[17]. Отсюда следует, что на границе ферромагнетика будут накапливаться те электроны, для которых химический потенциал больше[32], что можно представить в виде потенциала спиновой аккумуляции VAS, или так называемого интерфейсного сопротивления (присущего границе интерфейса ферромагнетик — немагнитный материал)
где j — плотность тока в образце, lsN и lsF — длины спиновой релаксации в немагнитном и магнитном материалах соответственно[33].
Методы получения[править | править код]
Материалы и экспериментальные данные[править | править код]
Можно подобрать достаточно много комбинаций веществ, которые будут обладать эффектом гигантского магнетосопротивления[34]. Некоторыми из часто использующихся и широко исследуемых являются следующие:
Величина магнетосопротивления зависит от многих параметров, таких как геометрия прибора (CIP или CPP), температура образца, толщина слоёв ферромагнитных и немагнитных материалов. При температуре 4,2 К и фиксированной толщине слоя кобальта в 1,5 нм изменение толщины слоя меди от 1 до 10 нм приводило к резкому уменьшению от 80 до 10 % в CIP-геометрии. В то же время с CPP-геометрией максимальный эффект на уровне 125 % достигался при dCu=2,5 нм. Увеличение до 10 нм приводило к уменьшению до 60 %. Зависимость имела осциллирующий характер[36].
Сверхрешётка из слоёв кобальта и меди толщинами 1,2 и 1,1 нм соответственно при изменении температуры от близкой к абсолютному нулю до 300 К демонстрировала уменьшение величины эффекта от 40 до 20 % в CIP-геометрии и от 100 до 55 % в CPP-геометрии[27].
Существуют исследования спиновых клапанов с неметаллическими немагнитными прослойками. В частности, для органических прослоек при 11 К фиксировалось гигантское негативное магнетосопротивление до 40 %[37]. Спиновые клапаны на графене различной конструкции демонстрировали ГМС на уровне 12 % при температуре 7 К и 10 % при температуре 300 К. Однако теоретические оценки позволяют предполагать верхнюю границу эффекта до 109 %[38].
К усилению эффекта приводит использование спиновых фильтров, поляризующих спины электронов во время прохождения электрического тока, которые изготавливаются из металлов наподобие кобальта. Для фильтра толщиной с длиной свободного пробега электронов наблюдалось изменение проводимости , которое можно записать как
где — изменение проводимости спинового клапана без фильтра, — максимальное увеличение проводимости при использовании фильтра, — параметр материала фильтра[39].
Типы ГМС[править | править код]
Классификацию часто производят по типам устройств, в которых проявляется эффект ГМС[40].
ГМС в плёнках[править | править код]
Антиферромагнитные сверхрешётки[править | править код]
Эффект ГМС в плёнках впервые наблюдался Фертом и Грюнбергом при исследовании сверхрешёток, состоящих из ферромагнитных и немагнитных слоёв. Толщина немагнитного слоя подбирается такая, чтобы взаимодействие между слоями было антиферромагнитным, и, как результат, основным состоянием была антипараллельная ориентация намагниченностей в соседних магнитных слоях. Тогда при внешнем воздействии, например, магнитным полем, ориентация векторов намагниченности в различных слоях может быть изменена на параллельную. Это сопровождается существенным изменением электрического сопротивления структуры[13].
Взаимодействие магнитных слоёв в подобных структурах происходит с помощью так называемого антиферромагнитного спаривания. Его следствием является осциллирующая зависимость коэффициента ГМС от толщины немагнитной прослойки. В первых сенсорах магнитного поля, использующих антиферромагнитные сверхрешётки, поле насыщения было очень большим (до десятков тысяч эрстед) вследствие сильного антиферромагнитного взаимодействия между применявшимися в них плёнками хрома и железа (кобальта), а также сильными полями анизотропии в них. Поэтому чувствительность подобных приборов была очень низкой. Позднее в них начали применять пермаллой (в магнитных слоях) и серебро (в немагнитных слоях), что снизило поле насыщения до десятков эрстед[41].
Спиновые клапаны на обменном смещении[править | править код]
Наиболее удачной оказалась конфигурация тех спиновых клапанов, в которых эффект ГМС возникает вследствие обменного смещения. Они состоят из сенсорного слоя, прослойки, «фиксированного» слоя и антиферромагнитно направленного фиксирующего слоя. Последний из них служит для фиксации направления намагниченности в «фиксированном» слое. Все слои, кроме фиксирующего, достаточно тонки для обеспечения низкого сопротивления структуры. Реакция на внешнее магнитное поле заключается в изменении направления намагниченности сенсорного слоя относительно «фиксированного»[42].
Основным отличием таких спиновых клапанов от других многослойных ГМС-устройств является монотонная зависимость амплитуды эффекта от толщины dN прослойки между магнитными слоями, что можно представить в виде феноменологической зависимости
где — некоторый нормировочный коэффициент ГМС, — длина свободного пробега электронов в немагнитном материале, d0 — эффективная толщина, учитывающая шунтирование остальных элементов структуры[40][43]. Можно привести подобное выражение для зависимости от толщины ферромагнитного слоя:
Смысл параметров формулы тот же, что и в предыдущей зависимости, но теперь для используемого ферромагнетика[34].
Многослойные структуры без связи (псевдоспиновые клапаны)[править | править код]
Эффект ГМС также может наблюдаться и в отсутствие антиферромагнитного спаривания слоями. В таком случае магнетосопротивление возникает из-за различия в коэрцитивных силах (например, меньшая у пермаллоя и бо́льшая у кобальта). В многослойных структурах типа пермаллой/медь/кобальт/медь внешнее магнитное поле приводит к переключению между различными направлениями намагниченности насыщения в слоях (параллельная при больших полях и антипараллельная в малых). Подобные системы характеризуются меньшим полем насыщения и бо́льшим , чем сверхрешётки с антиферромагнитной связью[42]. Также подобный эффект наблюдается в структурах кобальта и меди. Фактически, существование таких структур означает, что для наблюдения ГМС необходимым условием является не наличие связи между слоями, а некоторое распределение магнитного момента в структуре, которым можно управлять внешним полем[44].
Инверсный эффект ГМС[править | править код]
В случае инверсного эффекта минимум сопротивления наблюдается при антипараллельной ориентации намагниченности в слоях сверхрешётки. Инверсный эффект ГМС наблюдается, если магнитные слои состоят из различных материалов, например NiCr/Cu/Co/Cu. Если записать удельное сопротивление слоя для электронов с противоположными направлениями спинов в виде , то для никель-хромового и кобальтового слоёв знаки коэффициента спиновой асимметрии будут различны. При достаточной толщине слоя NiCr его вклад превысит вклад кобальтового слоя, что приведет к наблюдению инверсного эффекта[23]. Так как инверсия эффекта зависит лишь от знака произведения коэффициентов в соседних ферромагнитных слоях, а не от их знаков по отдельности, чтобы абстрагироваться от конкретного механизма взаимодействия спинов электронов с магнитными моментами атомов, иногда авторами оговаривается знак , что учитывается в последующем изложении[27].
Известно, что аналогичные никель-хромовому слою свойства будет проявлять никель, легированный ванадием, в то время как легирование железом, кобальтом, марганцем, золотом или медью не приведет к наблюдению инверсного эффекта в рассмотренной выше структуре[45].
ГМС в зернистых структурах[править | править код]
ГМС в зернистых сплавах (до десятков нанометров) ферромагнитных и немагнитных металлов было обнаружено в 1992 году и впоследствии объяснено спин-зависимым рассеянием носителей тока на поверхности и в объёме гранул. Гранулы образуют ферромагнитные кластеры обычно диаметром порядка 10 нм, окружённые немагнитным металлом, что может быть описано как эффективная плёночная сверхрешётка. Необходимым условием для материалов таких сплавов является плохая взаимная растворимость компонентов (например, кобальт и медь). На свойства таких структур сильно влияет время и температура отжига: можно получить отрицательное ГМС, которое увеличивается при увеличении температуры[35][46].
Применение[править | править код]
Датчики на спиновых клапанах[править | править код]
Общая схема[править | править код]

Одной из основных сфер применения ГМС является измерительная техника: на базе эффекта были созданы датчики магнитного поля различного назначения (в считывающих головках накопителей на жёстких магнитных дисках, где происходит определение направления магнитного поля в ячейке, хранящей бит информации[26], биосенсорах[34], средствах детекции и измерения колебаний в МЭМС[34] и др.). Типичный датчик, использующий эффект ГМС, состоит из семи слоёв:
- Кремниевая подложка.
- Связующий слой.
- Сенсорный (нефиксированный, движимый) слой.
- Немагнитный слой.
- Фиксирующий (пиннинговый) слой.
- Антиферромагнитный (фиксированный) слой.
- Защитный слой.
В качестве связующего и защитного слоёв часто используют тантал, а немагнитной прослойкой служит медь. В сенсорном слое намагниченность может свободно ориентироваться внешним магнитным полем. Он изготавливается из соединения NiFe или кобальтовых сплавов. Антиферромагнитный слой изготавливается из плёнок FeMn или NiMn. Направление намагниченности в нём определяется фиксирующим слоем из магнитотвёрдого материала, например, кобальта. Такой датчик характеризуется асимметричной петлёй Гистерезиса, что связано с наличием магнитотвёрдого слоя, фиксирующего направление намагниченности в рабочем диапазоне полей[47][48].
В спиновых клапанах также наблюдается анизотропное магнетосопротивление, которое приводит к асимметрии кривой чувствительности. Его учёт даёт значение магнетосопротивления, очень хорошо совпадающее с наблюдаемым на практике[49].
Реализация в жёстких магнитных дисках[править | править код]
В жёстких магнитных дисках (HDD) информация кодируется с помощью магнитных доменов, когда одному направлению намагниченности в них ставится в соответствие логическая единица, а противоположному — логический нуль. Различают продольный и перпендикулярный методы записи.
В продольном методе домены располагаются в плоскости пластины, то есть направление в них параллельно поверхности. Между доменами всегда формируется переходная область (доменная стенка), в области которой на поверхность выходит магнитное поле. Если доменная стенка образовалась на границе двух северных полюсов доменов, то поле направлено наружу, а если её образовали южные полюса — то внутрь. Чтобы считать направление магнитного поля над доменной стенкой, в антиферромагнитном слое датчика фиксируется направление намагниченности перпендикулярно плоскости пластины диска, а в сенсорном слое - параллельно ей. Изменение направления внешнего магнитного поля отклоняет намагниченность в сенсорном слое от равновесного положения вверх или вниз. Когда направление отклонения совпадает с направлением в фиксированном слое, электрическое сопротивление датчика уменьшается, и наоборот, при различных направлениях детектируется увеличение сопротивления. Таким образом определяется взаимная ориентация доменов, над которыми прошла считывающая головка[50].
В настоящее время широко используется вертикальное расположение доменов, что позволяет существенно увеличить плотность размещения битов на поверхности пластины[51]. При этом на поверхность выходит поле, образуемое самим доменом.
Магнитная оперативная память[править | править код]

Ячейка магниторезистивной оперативной памяти (англ. magnetic random-access memory, MRAM) состоит из структуры, подобной датчику на спиновом клапане. Значение хранимого бита может кодироваться направлением намагниченности в сенсорном слое, в данном случае выступающем в качестве носителя информации. Считывание происходит путём измерения сопротивления структуры. Преимущества подобной технологии состоят вне зависимости от источников питания[К 2], низком энергопотреблении и высоком быстродействии[26].
В типичным блоке памяти на основе магниторезистивного эффекта, хранящем один бит информации, ГМС-структура формата CIP размещается между двумя проводниками, ориентированными перпендикулярно по отношению друг к другу. Эти проводники называются линиями строк и столбцов. Импульсы электрического тока, проходящие через линии, генерируют вихревое магнитное поле, которое воздействует на ГМС-структуру. Контуры силовых линий поля по форме близки к эллипсам, а направление поля (по или против часовой стрелки) определяется направлением тока по линии. При этом используется ГМС-структура, намагниченность внутри которой ориентирована вдоль линии строки.
Таким образом, направление поля, создаваемого линией столбца, направлено практически параллельно магнитным моментам, и оно не может их развернуть. Линия строки создаёт поле, перпендикулярное им, и, вне зависимости от величины поля, может повернуть намагниченность только на 90°. При одновременном прохождении импульсов по линиям строк и столбцов суммарное магнитное поле в месте расположения структуры ГМС будет направлено под острым углом по отношению к одним моментам и под тупым по отношению к другим. Если величина поля превысит некоторую критическую величину, последние изменят своё направление.
Применяются различные схемы хранения и считывания информации из описанной ячейки. В одной из них информация хранится в движимом слое структуры. Тогда операция чтения определяет, изменилось ли сопротивление структуры при приложении магнитного поля. При этом считанный бит стирается, и его нужно записать в ячейку вновь. В другой схеме информацию хранит фиксированный слой, что требует бо́льших токов для записи по сравнению с токами считывания[52].
На сегодняшний день в случае MRAM гигантский магниторезистивный эффект уступил место туннельному[53]. В подобных структурах также необходимы вентильные элементы, предотвращающие блуждающие токи между ячейками памяти. Таким вентильным элементом может быть МОП-транзистор, к стоку которого подключается ГМС-структура, к истоку — заземление, а к затвору — одна из линий, служащих для считывания[54].
Другие применения[править | править код]
Магниторезистивные изоляторы для бесконтактной передачи сигнала между двумя гальванически изолированными частями электрических схем впервые были продемонстрированы в 1997 году как альтернатива оптопарам благодаря лучшей интегрируемости. Мост Уитстона из четырёх одинаковых ГМС-устройств нечувствителен к однородному магнитному полю, реагируя лишь тогда, когда направления полей антипараллельны в соседних ножках моста. Подобные устройства, продемонстрированные в 2003 году, могут использоваться в качестве выпрямителей тока с линейной АЧХ. Обобщённая до четырёх независимых токов схема подобного моста (транспинор, англ. transpinnor) была сделана Сионгте Баи в 2002 году и может использоваться в качестве логического вентиля[34][55].
См. также[править | править код]
- Спинтроника
- Полуметалл (спинтроника)
- РККИ-обменное взаимодействие
- Магнетосопротивление
- Анизотропное магнетосопротивление
- Колоссальное магнетосопротивление
- Туннельное магнетосопротивление
Примечания[править | править код]
Комментарии[править | править код]
- ↑ Схема не отображает наличие магнитного гистерезиса, так как форма его петли в сверхрешётке существенно зависит от толщины немагнитного слоя. В опытах Ферта хорошо выраженный гистерезис с полем насыщения около 4 кГс и остаточной намагниченностью, составляющей около 60 % от намагниченности насыщения, наблюдался при толщине немагнитной прослойки, равной нм. Но при уменьшении до значения 0,9 нм, соответствующего наибольшему достигнутому ГМС, петля редуцировалась до узкой вытянутой фигуры с полем насыщения 20 кГс и малой остаточной намагниченностью (см. Baibich M. N et al. Giant Magnetoresistance of (001)Fe/(001)Cr Magnetic Superlattices (неопр.) // PRL. — 1988. — Т. 61, № 21. — С. 2472—2475. — doi:10.1103/PhysRevLett.61.2472.)
- ↑ Сохранение состояния ячейки, хранящей один бит информации, при отключении питания является возможным благодаря наличию потенциального барьера, который необходимо преодолеть для переориентации направления намагниченности в свободном (сенсорном) слое при переходе между параллельными и антипараллельными состояниями структуры (см. Denny D. Tang, Yuan-Jen Lee. Magnetic Memory: Fundamentals and Technology. — Cambridge University Press, 2010. — P. 103. — 208 p. — ISBN 978-0521449649.).
Источники[править | править код]
- ↑ 1 2 3 4 5 6 Никитин С. А. Гигантское магнитосопротивление // Соросовский обозревательный журнал. — 2004. — Т. 8, № 2. — С. 92—98. Архивировано 28 января 2022 года.
- ↑ 1 2 Э. Л. Нагаев. Манганиты лантана и другие магнитные проводники с гигантским магнитосопротивлением // Успехи физических наук. — Российская академия наук, 1996. — Т. 166, № 8. — С. 833—858. — doi:10.3367/UFNr.0166.199608b.0833. Архивировано 14 сентября 2013 года.
- ↑ Colossal Magnetoresistance, Charge Ordering and Related Properties of Manganese Oxides / Ed. by C. N. R. Rao and B. Raveau. — World Scientfic Publishing Co, 1998. — P. 2. — 356 p. — ISBN 978-981-02-3276-4.
- ↑ Hirota, E., Sakakima, H., Inomata, K. Giant Magneto-Resistance Devices. — Springer, 2002. — P. 30. — 177 p. — ISBN 978-3-540-41819-1.
- ↑ Я. М. Муковский. Получение и свойства материалов с колоссальным магнетосопротивлением // Рос. хим. ж. — 2001. — Т. XLV, № 5—6. — С. 32—41. Архивировано 18 октября 2012 года.
- ↑ Alfred Brian Pippard. Magnetoresistance in Metals. — Cambridge University Press, 2009. — Vol. 2. — P. 8. — 268 p. — (Cambridge Studies in Low Temperature Physics). — ISBN 9780521118804.
- ↑ 1 2 3 4 5 6 7 8 Claude Chappert, Albert Fert and Frédéric Nguyen Van Dau. The emergence of spin electronics in data storage (англ.) // Nature Materials : journal. — 2007. — Vol. 6. — P. 813—823. — doi:10.1038/nmat2024. Архивировано 20 ноября 2016 года.
- ↑ Hirota, E., Sakakima, H., Inomata, K. Giant Magneto-Resistance Devices. — Springer, 2002. — P. 23. — 177 p. — ISBN 978-3-540-41819-1.
- ↑ The Nobel Prize in Physics 2007 (англ.). The Official Web Site of the Nobel Prize. Дата обращения: 27 февраля 2011. Архивировано 10 августа 2011 года.
- ↑ Frederick Seitz, David Turnbull. Advances in Research and Applications. — Academic Press, 1957. — Vol. 5. — P. 31. — 455 p. — (Solid State Physics). — ISBN 978-0126077056.
- ↑ Aboaf J. A. New Magnetoresistive Materials (англ.) (недоступная ссылка — история) (9 октября 1984). — United States Patent No. 4476454. Дата обращения: 11 апреля 2011.
- ↑ 1 2 Ферт А. Происхождение, развитие и перспективы спинтроники // УФН. — 2008. — Т. 178, № 12. — С. 1336—1348. — doi:10.3367/UFNr.0178.200812f.1336. Архивировано 19 августа 2011 года.
- ↑ 1 2 3 4 5 M. N. Baibich, J. M. Broto, A. Fert, F. Nguyen Van Dau, F. Petroff, P. Eitenne, G. Creuzet, A. Friederich, and J. Chazelas. Giant Magnetoresistance of (001)Fe/(001)Cr Magnetic Superlattices (англ.) // Physical Review Letters : journal. — 1988. — Vol. 61, no. 21. — P. 2472—2475. — doi:10.1103/PhysRevLett.61.2472.
- ↑ Tsymbal E. Y. and Pettifor D. G. Perspectives of Giant Magnetoresistance // Solid state physics / Ed. by Henry Ehrenreich, Frederick Seitz, David Turnbull, Frans Spaepen. — Academic Press, 2001. — Vol. 56. — P. 120. — 483 p. — (Solid State Physics: Advances in Research and Applications). — ISBN 9780126077568.
- ↑ R. E. Camley and J. Barnaś. Theory of giant magnetoresistance effects in magnetic layered structures with antiferromagnetic coupling (англ.) // Phys. Rev. Lett : journal. — 1989. — Vol. 63, no. 6. — P. 664—667. — doi:10.1103/PhysRevLett.63.664.
- ↑ Peter M. Levy, Shufeng Zhang, Albert Fert. Electrical conductivity of magnetic multilayered structures (англ.) // Phys. Rev. Lett : journal. — 1990. — Vol. 65, no. 13. — P. 1643—1646. — doi:10.1103/PhysRevLett.65.1643.
- ↑ 1 2 T. Valet, A. Fert. Theory of the perpendicular magnetoresistance in magnetic multilayers (англ.) // Physical Review B : journal. — 1993. — Vol. 48, no. 10. — P. 7099—7113. — doi:10.1103/PhysRevB.48.7099.
- ↑ Nagasaka K. et al. CPP-GMR Technology for Future High-Density Magnetic Recording (англ.). Fujitsu (30 июня 2005). Дата обращения: 11 апреля 2011. Архивировано 10 августа 2011 года.
- ↑ K. H. J. Buschow. Concise encyclopedia of magnetic and superconducting materials. — 2nd. — Elsevier, 2005. — P. 580. — 1339 p. — ISBN 9780080445861.
- ↑ Tsymbal E. Y. and Pettifor D. G. Perspectives of Giant Magnetoresistance // Solid state physics / Ed. by Henry Ehrenreich, Frederick Seitz, David Turnbull, Frans Spaepen. — Academic Press, 2001. — Vol. 56. — P. 122. — 483 p. — (Solid State Physics: Advances in Research and Applications). — ISBN 9780126077568.
- ↑ Tsymbal E. Y. and Pettifor D. G. Perspectives of Giant Magnetoresistance // Solid state physics / Ed. by Henry Ehrenreich, Frederick Seitz, David Turnbull, Frans Spaepen. — Academic Press, 2001. — Vol. 56. — P. 126—132. — 483 p. — (Solid State Physics: Advances in Research and Applications). — ISBN 9780126077568.
- ↑ Савельев И. В. Электричество и магнетизм // Курс общей физики. — М.: Астрель АСТ, 2004. — Т. 2. — С. 271—274. — 336 с. — 5000 экз. — ISBN 5-17-003760-0.
- ↑ 1 2 K. H. J. Buschow. Concise encyclopedia of magnetic and superconducting materials. — 2nd. — Elsevier, 2005. — P. 254. — 1339 p. — ISBN 9780080445861.
- ↑ Stöhr, J. and Siegmann, H. C. Magnetism: From Fundamentals to Nanoscale Dynamics. — Springer-Verlag Berlin Heidelberg, 2006. — P. 638. — 820 p. — ISBN 978-3540302827.
- ↑ J. Inoue, T. Tanaka and H. Kontani. Anomalous and spin Hall effects in magnetic granular films (англ.) // Physical Review B : journal. — 2009. — Vol. 80, no. 2. — P. 020405(R). — doi:10.1103/PhysRevB.80.020405.
- ↑ 1 2 3 4 к.ф.-м.н. А. В. Хвальковский. Гигантское магнитосопротивление: от открытия до Нобелевской премии. AMT&C. Дата обращения: 27 февраля 2011. Архивировано из оригинала 8 января 2015 года.
- ↑ 1 2 3 Bass, J., Pratt, W. P. Current-perpendicular (CPP) magnetoresistance in magnetic metallic multilayers (англ.) // JMMM : journal. — 1999. — Vol. 200. — P. 274—289. — doi:10.1016/S0304-8853(99)00316-9.
- ↑ О. В. Третяк, В. А. Львов, О. В. Барабанов. Фізичні основи спінової електроніки. — К.: Київський університет, 2002. — С. 243. — 314 с. — ISBN 966-594-323-5.
- ↑ О. В. Третяк, В. А. Львов, О. В. Барабанов. Фізичні основи спінової електроніки. — К.: Київський університет, 2002. — С. 258—261, 247—248. — 314 с. — ISBN 966-594-323-5.
- ↑ О. В. Третяк, В. А. Львов, О. В. Барабанов. Фізичні основи спінової електроніки. — К.: Київський університет, 2002. — С. 258—261. — 314 с. — ISBN 966-594-323-5.
- ↑ О. В. Третяк, В. А. Львов, О. В. Барабанов. Фізичні основи спінової електроніки. — К.: Київський університет, 2002. — С. 247—248. — 314 с. — ISBN 966-594-323-5.
- ↑ Stöhr, J. and Siegmann, H. C. Magnetism: From Fundamentals to Nanoscale Dynamics. — Springer-Verlag Berlin Heidelberg, 2006. — P. 641. — 820 p. — ISBN 978-3540302827.
- ↑ Stöhr, J. and Siegmann, H. C. Magnetism: From Fundamentals to Nanoscale Dynamics. — Springer-Verlag Berlin Heidelberg, 2006. — P. 648—649. — 820 p. — ISBN 978-3540302827.
- ↑ 1 2 3 4 5 6 R. Coehoorn. Novel Magnetoelectronic Materials and Devices (англ.). Giant magnetoresistance and magnetic interactions in exchange-biased spin-valves. Lecture Notes. Technische Universiteit Eindhoven (2003). Дата обращения: 25 апреля 2011. Архивировано 10 августа 2011 года.
- ↑ 1 2 А. Б. Грановский, М. Ильин, А. Жуков, В. Жукова, Х. Гонзалес. Гигантское магнитосопротивление гранулированных микропроводов: спин-зависящее рассеяние в межгранульных промежутках // ФТТ. — 2011. — Т. 53, № 2. — С. 299—301. Архивировано 20 августа 2014 года.
- ↑ K. H. J. Buschow. Concise encyclopedia of magnetic and superconducting materials. — 2nd. — Elsevier, 2005. — P. 248. — 1339 p. — ISBN 9780080445861.
- ↑ Dali Sun, Lifeng Yin, Chengjun Sun, Hangwen Guo, Zheng Gai, X.-G. Zhang, T. Z. Ward, Zhaohua Cheng, and Jian Shen. Giant Magnetoresistance in Organic Spin Valves (англ.) // Phys. Rev. Lett : journal. — 2010. — Vol. 104, no. 23. — P. 236602. — doi:10.1103/PhysRevLett.104.236602.
- ↑ Rui Qin, Jing Lu, Lin Lai, Jing Zhou, Hong Li, Qihang Liu, Guangfu Luo, Lina Zhao, Zhengxiang Gao, Wai Ning Mei, and Guangping Li. Room-temperature giant magnetoresistance over one billion percent in a bare graphene nanoribbon device (англ.) // Physical Review B : journal. — 2010. — Vol. 81, no. 23. — P. 233403. — doi:10.1103/PhysRevB.81.233403.
- ↑ Ultrathin Magnetic Structures / Ed. by B. Heinrich and J. A. C. Bland. — Springer, 2005. — Vol. IV. — P. 161—163. — 257 p. — (Application of Nanomagnetism). — ISBN 978-3-540-21954-5.
- ↑ 1 2 Evgeny Tsymbal. GMR Structures (англ.). University of Nebraska-Lincoln. Дата обращения: 11 апреля 2011. Архивировано 10 августа 2011 года.
- ↑ Hari Singh Nalwa. Handbook of thin film materials: Nanomaterials and magnetic thin films. — Academic Press, 2002. — Vol. 5. — P. 518—519. — 633 p. — ISBN 9780125129084.
- ↑ 1 2 Hari Singh Nalwa. Handbook of thin film materials: Nanomaterials and magnetic thin films. — Academic Press, 2002. — Vol. 5. — P. 519. — 633 p. — ISBN 9780125129084.
- ↑ Hari Singh Nalwa. Handbook of thin film materials: Nanomaterials and magnetic thin films. — Academic Press, 2002. — Vol. 5. — P. 519, 525—526. — 633 p. — ISBN 9780125129084.
- ↑ Pu F. C. Aspects of Modern Magnetism: Lecture Notes of the Eighth Chinese International Summer School of Physics Beijing, China 28 August-7 September, 1995 / Ed. by Y. J. Wang, C. H. Shang. — World Scientific Pub Co Inc, 1996. — P. 122. — 271 p. — ISBN 978-9810226015.
- ↑ Guimarães, Alberto P. Principles of Nanomagnetism. — Springer, 2009. — P. 132. — 224 p. — ISBN 978-3-642-01481-9.
- ↑ Magnetic Domains in Granular GMR Materials. National Institute of Standards and Technology. Дата обращения: 12 марта 2011. Архивировано 10 августа 2011 года.
- ↑ Elliot Brown and Matthew Wormington. An Investigation of Giant Magnetoresistance (GMR) Spinvalve Structures Using X-Ray Diffraction and Reflectivity. The International Centre for Diffraction Data. Дата обращения: 12 марта 2011. Архивировано 10 августа 2011 года.
- ↑ B. C. Dodrill, B. J. Kelley. Magnetic In-line Metrology for GMR Spin-Valve Sensors. Lake Shore Cryotronics, Inc.. Дата обращения: 12 марта 2011. Архивировано 10 августа 2011 года.
- ↑ Magnetic Multilayers and Giant Magnetoresistance / Ed. by U. Hartmann. — Springer, 2000. — Vol. 37. — P. 111. — 321 p. — (Springer Series in Surface Sciences). — ISBN 978-3-540-65568-8.
- ↑ О. В. Третяк, В. А. Львов, О. В. Барабанов. Фізичні основи спінової електроніки. — К.: Київський університет, 2002. — С. 285—286. — 314 с. — ISBN 966-594-323-5.
- ↑ Мартин Егер. «Разрушаем мифы»: магнитное поле и HDD. Chip Online UA (26 апреля 2011). Дата обращения: 30 апреля 2011. Архивировано 10 августа 2011 года.
- ↑ О. В. Третяк, В. А. Львов, О. В. Барабанов. Фізичні основи спінової електроніки. — К.: Київський університет, 2002. — С. 289—291. — 314 с. — ISBN 966-594-323-5.
- ↑ Зайцев Д. Д. Магнетосопротивление, Туннельное. Словарь нанотехнологических и связанных с нанотехнологиями терминов. Роснано. Дата обращения: 11 апреля 2011. Архивировано 10 августа 2011 года.
- ↑ Denny D. Tang, Yuan-Jen Lee. Magnetic Memory: Fundamentals and Technology. — Cambridge University Press, 2010. — P. 93—95. — 208 p. — ISBN 978-0521449649.
- ↑ Torok, E. J.; Zurn, S.; Sheppard, L. E.; Spitzer, R.; Seongtae Bae; Judy, J. H.; Egelhoff, W. F. Jr.; Chen, P. J. „Transpinnor“: A new giant magnetoresistive spin-valve device (неопр.) // INTERMAG Europe 2002. Digest of Technical Papers. 2002 IEEE International. — 2002. — С. AV8. — ISBN 0-7803-7365-0. — doi:10.1109/INTMAG.2002.1000768.
Литература[править | править код]
Статьи[править | править код]
- Ферт А. Происхождение, развитие и перспективы спинтроники // УФН. — 2008. — Т. 178, № 12. — С. 1336—1348. — doi:10.3367/UFNr.0178.200812f.1336.
- P. Grünberg, R. Schreiber, Y. Pang, M. B. Brodsky, and H. Sowers. Layered Magnetic Structures: Evidence for Antiferromagnetic Coupling of Fe Layers across Cr Interlayers (англ.) // Physical Review Letters : journal. — 1986. — Vol. 57, no. 19. — P. 2442—2445. — doi:10.1103/PhysRevLett.57.2442. — PMID 10033726.
- A. Vedyayev, M. Chshiev, N. Ryzhanova, B. Dieny, C. Cowache and F. Brouers. A unified theory of CIP and CPP giant magnetoresistance in magnetic sandwiches (англ.) // JMMM : journal. — 1997. — Vol. 172, no. 1—2. — P. 53—60. — doi:10.1016/S0304-8853(97)00081-4.
- Bazaliy, Y. B., Jones, B. A. and Zhang, S.-C. Modification of the Landau-Lifshitz equation in the presence of a spin-polarized current in colossal- and giant-magnetoresistive materials (англ.) // PRB : journal. — 1998. — Vol. 57, no. 6. — P. R3213—R3216. — doi:10.1016/S0304-8853(97)00081-4.
Книги[править | править код]
- Hirota, E., Sakakima, H., Inomata, K. Giant Magneto-Resistance Devices. — Springer, 2002. — 177 p. — ISBN 978-3-540-41819-1.
- Adrian D. Torres, Daniel A. Perez. Giant Magnetoresistance: New Research. — Nova Science Publishers, 2008. — 289 p. — ISBN 9781604567335.
- Nicola A. Spaldin. Magnetic Materials: Fundamentals and Applications. — 2nd ed. — Cambridge University Press: 2010. — 288 p. — ISBN 9780521886697.
- Peter R. Savage. Giant Magnetoresistance: Technology and Markets for Sensors, Disk Storage, Mram, and Spintronics. — John Wiley & Sons Inc, 2000. — Vol. 276. — 136 p. — (Technical insights). — ISBN 9780471414162.
Ссылки[править | править код]
- О. Баклицкая. Нобелевские премии 2007 года. Гигантское магнетосопротивление — триумф фундаментальной науки. Наука и жизнь. Дата обращения: 27 февраля 2011. Архивировано из оригинала 25 марта 2012 года.
- И. Иванов. Нобелевская премия по физике — 2007. Элементы.ру (16 октября 2007). Дата обращения: 27 апреля 2011. Архивировано 10 августа 2011 года.
- Современные магнитные носители информации. Устройства магнитной записи и воспроизведения. Магнитооптические носители информации. Научно-исследовательский институт ядерной физики им. Д. В. Скобельцына. Дата обращения: 30 апреля 2011. Архивировано 10 августа 2011 года.
- Jose Ignacio Pascual. Magnetism and magnetic materials (англ.). Freie Universität Berlin. — Презентация, посвящённая основам магнетизма и эффекту гигантского магнетосопротивления. Дата обращения: 14 мая 2011. Архивировано 10 августа 2011 года.
- Нобелевское сопротивление: Премия за жесткие диски. Журнал «Популярная механика» (10 октября 2007). Дата обращения: 29 июня 2011. Архивировано из оригинала 19 февраля 2012 года.
Эта статья входит в число избранных статей русскоязычного раздела Википедии. |















![{\displaystyle \theta \in [-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb953905c1f4461b83fe73f5a00e751727ddd73b)











![{\displaystyle R_{\uparrow \downarrow }^{CIP}={\frac {L}{2(2a+b)S}}\left[a(\rho _{F+}+\rho _{F-})+b\rho _{N}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62c4a76ec88f343666ce00869f762d3b95d513e7)























