Равномерно темперированный строй

Равноме́рно темпери́рованный строй, равномерная темперация (нем. gleichschwebende Temperatur, gleichschwebende Stimmung) — темперированный музыкальный строй, в котором каждая октава делится на математически равные интервалы, в наиболее типичном случае — на двенадцать полутонов, каждый из которых равен ${\sqrt[{12}]{2}}$ . Такой строй господствует в европейской профессиональной музыке (академической и эстрадной) начиная с XVIII века до наших дней. Важным преимуществом равномерной темперации является возможность транспонирования пьесы на произвольный интервал.

Исторический очерк

Равномерно темперированный строй возник в обстановке поисков учёными разных специальностей «идеального» для музыки строя. Исторически предшествующие чистый и среднетоновый строи не позволяли транспонировать и модулировать в отдалённые тональности без того, чтобы в консонирующих созвучиях — прежде всего, в трезвучиях и их обращениях — не возникал резкий акустический диссонанс.

Непосредственным предшественником равномерно темперированного строя в Европе был «хорошо темперированный» строй — семейство неравномерных темпераций, позволявших более или менее успешно (с разной степенью «акустической чистоты») играть в любой из тональностей. Одним из теоретиков и пропагандистов^[1] такого строя был Андреас Веркмейстер. Многие исследователи разделяют мнение, что «Хорошо темперированный клавир» Иоганна Себастьяна Баха, хорошо знакомого с работами Веркмейстера, написан для инструментов именно с такой неравномерной темперацией^[2].

Невозможно с достоверностью указать, кто именно «изобрёл» равномерную темперацию. Среди первых её теоретиков называют Генриха Грамматеуса (1518), Винченцо Галилея (1581) и Марена Мерсенна. Симон Стевин в своём труде «О теории певческого искусства» (ок. 1585) дал математически точный расчёт равномерной темперации. Написанная на родном языке Стевина (фламандском) его работа не получила резонанса; посмертная слава пришла к Стевину спустя 300 лет, в 1884 году, когда она была опубликована и затем переведёна на другие языки.

Одним из первых авторов, давших теоретическое обоснование 12-ступенной равномерной темперации, был китайский принц Чжу Цзайюй (朱載堉), в трактате 1584 года^[3]. Однако, какое практическое значение расчёты принца имели для западной музыкально-теоретической традиции, неизвестно.

У нового строя были свои оппоненты (например, Джузеппе Тартини) и свои пропагандисты (особенно Иоганн Георг Нейдхардт). Равномерно темперированный строй вызывал отклонения от акустической («природной») чистоты созвучий, в результате в них появились небольшие биения. По мнению одних, эти нарушения чистоты были незначительной потерей, особенно с учётом новых возможностей, которые такой строй давал развитию тональной гармонии. Другие же рассматривали потерю «природной» чистоты как посягательство на «чистоту» музыки.

Противоречивость эстетических критериев (природная чистота против модуляционной свободы и неограниченной транспозиции) отражалась в трудах теоретиков музыки. Так, Веркмейстер утверждал, что в новом строе все аккорды (подразумевались прежде всего трезвучия) приобретают монотонную симметрию, в то время как в «хороших» строях каждый аккорд имел своё неповторимое (акустическое) звучание. С другой стороны, он же в позднем трактате «Musikalische Paradoxal-Discourse» (1707) в полемике с Нейдхардтом защищал свой приоритет в «изобретении» равномерно темперированного строя. Уже в XVIII веке идея свободного развёртывания тональности одержала верх над идеей природной «акустической» чистоты. В академической и эстрадной музыке равномерная темперация получила мировое признание и стала фактическим стандартом музыкального строя.

Вычисление частот звуков

Можно математически вычислить частоты для всего звукоряда, пользуясь формулой:

f(i)=f_{0}\cdot 2^{i/12}

,

где f₀ — частота камертона (например Ля 440 Hz), а i — количество полутонов в интервале от исследуемого звука к эталону f₀.

Последовательность вычисленных таким образом частот образует геометрическую прогрессию:

например, можно вычислить частоту звука на тон (2 полутона) ниже от камертона Ля — ноты соль:

i=-2

f(-2)=440\,\mathrm {Hz} \cdot 2^{-2/12}\approx {391,995}\,\mathrm {Hz}

если надо вычислить частоту ноты Соль, но на октаву (12 полутонов) выше:

i=12-2=10

f(10)=440\,\mathrm {Hz} \cdot 2^{10/12}\approx {783,991}\,\mathrm {Hz}

Частоты двух полученных нот Соль отличаются в два раза, что дает чистую октаву.

Сравнение с натуральным строем

Равномерно темперированный строй можно отобразить в виде значений интервалов в центах:

Тон	C¹	C♯	D	D♯	E	F	F♯	G	G♯	A	A♯	B	C²
Цент	0	100	200	300	400	500	600	700	800	900	1000	1100	1200

Следующая таблица показывает количественные отличия интервалов равномерно темперированного ряда от натуральных интервалов:

Интервал	Равномерно темперированные интервалы	Натуральные интервалы	Разница в центах
Прима	${\sqrt[{12}]{2^{0}}}=1=0\,$ центов	${\frac {1}{1}}=1=0\,$ центов	0
Малая секунда	${\sqrt[{12}]{2^{1}}}={\sqrt[{12}]{2}}\approx 1{,}059463=100\,$ центов	${\frac {16}{15}}\approx 1{,}066667\approx 111{,}73\,$ центов	−11,73
Большая секунда	${\sqrt[{12}]{2^{2}}}={\sqrt[{6}]{2}}\approx 1{,}122462=200\,$ центов	${\frac {9}{8}}=1{,}125\approx 203{,}91\,$ центов	−3,91
Малая терция	${\sqrt[{12}]{2^{3}}}={\sqrt[{4}]{2}}\approx 1{,}189207=300\,$ центов	${\frac {6}{5}}=1{,}2\approx 315{,}64\,$ центов	−15,64
Большая терция	${\sqrt[{12}]{2^{4}}}={\sqrt[{3}]{2}}\approx 1{,}259921=400\,$ центов	${\frac {5}{4}}=1{,}25\approx 386{,}31\,$ центов	13,69
Кварта	${\sqrt[{12}]{2^{5}}}={\sqrt[{12}]{32}}\approx 1{,}334840=500\,$ центов	${\frac {4}{3}}\approx 1{,}333333\approx 498{,}04\,$ центов	1,96
Тритон	${\sqrt[{12}]{2^{6}}}={\sqrt {2}}\approx 1{,}414214=600\,$ центов	${\frac {45}{32}}\approx 1{,}406250\approx 590{,}22\,$ центов	9,78
Квинта	${\sqrt[{12}]{2^{7}}}={\sqrt[{12}]{128}}\approx 1{,}498307=700\,$ центов	${\frac {3}{2}}=1{,}5\approx 701{,}96\,$ центов	−1,96
Малая секста	${\sqrt[{12}]{2^{8}}}={\sqrt[{3}]{4}}\approx 1{,}587401=800\,$ центов	${\frac {8}{5}}=1{,}6\approx 813{,}69\,$ центов	−13,69
Большая секста	${\sqrt[{12}]{2^{9}}}={\sqrt[{4}]{8}}\approx 1{,}681793=900\,$ центов	${\frac {5}{3}}\approx 1{,}666667\approx 884{,}36\,$ центов	15,64
Малая септима	${\sqrt[{12}]{2^{10}}}={\sqrt[{6}]{32}}\approx 1{,}781797=1000\,$ центов	${\frac {16}{9}}\approx 1{,}777778\approx 996{,}09\,$ центов	3,91
Большая септима	${\sqrt[{12}]{2^{11}}}={\sqrt[{12}]{2048}}\approx 1{,}887749=1100\,$ центов	${\frac {15}{8}}=1{,}875\approx 1088{,}27\,$ центов	11,73
Октава	${\sqrt[{12}]{2^{12}}}=2=1200\,$ центов	${\frac {16}{8}}=2=1200\,$ центов	0

Расчётные частоты для клавиатуры фортепиано

Примечания

Значения частот рассчитаны исходя из стандартной частоты камертона ля¹ = 440 Гц.
О феномене неточного равенства рассчитанных и реальных частот настроенного фортепиано (расширения интервалов на краях диапазона), см. Кривые Рейлсбека.

Субконтроктава

Охватывает звуки с частотами от 16,352 Гц (включительно) до 32,703 Гц. Наименования ступеней записываются с большой буквы и справа снизу ставится цифра 2 (или два штриха). В научной нотации имеет номер 0.

Номер ступени	Частота, Гц	Слоговое обозначения по Гельмгольцу	Буквенное обозначение по Гельмгольцу	Американская нотация	Координатно-частотная нотация
1	16,352	До₂	C₂	C0	-52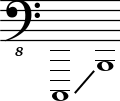
2	18,354	Ре₂	D₂	D0	-50
3	20,602	Ми₂	E₂	E0	-48
4	21,827	Фа₂	F₂	F0	-47
5	24,500	Соль₂	G₂	G0	-45
6	27,500	Ля₂	A₂	A0	-43
7	30,868	Си₂	H₂	B0	-41

Контроктава

Охватывает звуки с частотами от 32,703 Гц (включительно) до 65,406 Гц. Наименования ступеней записываются с большой буквы и справа снизу ставится цифра 1 (или один штрих). В научной нотации имеет номер 1.

Номер ступени	Частота, Гц	Слоговое обозначения по Гельмгольцу	Буквенное обозначение по Гельмгольцу	Американская нотация	Координатно-частотная нотация
1	32,703	До₁	C₁	C1	-40
2	36,708	Ре₁	D₁	D1	-38
3	41,203	Ми₁	E₁	E1	-36
4	43,654	Фа₁	F₁	F1	-35
5	48,999	Соль₁	G₁	G1	-33
6	55,000	Ля₁	A₁	A1	-31
7	61,735	Си₁	H₁	B1	-29

Большая октава

Охватывает звуки с частотами от 65,406 Гц (включительно) до 130,81 Гц. Наименования ступеней записываются с большой буквы без дополнительных цифр или штрихов. В научной нотации имеет номер 2.

Номер ступени	Частота, Гц	Слоговое обозначения по Гельмгольцу	Буквенное обозначение по Гельмгольцу	Американская нотация	Координатно-частотная нотация
1	65,406	До	C	C2	-28
2	73,416	Ре	D	D2	-26
3	82,406	Ми	E	E2	-24
4	87,307	Фа	F	F2	-23
5	97,999	Соль	G	G2	-21
6	110,00	Ля	A	A2	-19
7	123,47	Си	H	B2	-17

Малая октава

Охватывает звуки с частотами от 130,81 Гц (включительно) до 261,63 Гц. Наименования ступеней записываются с маленькой буквы без дополнительных цифр или штрихов. В научной нотации имеет номер 3.

Номер ступени	Частота, Гц	Слоговое обозначения по Гельмгольцу	Буквенное обозначение по Гельмгольцу	Американская нотация	Координатно-частотная нотация
1	130,81	до	c	C3	-16
2	146,83	ре	d	D3	-14
3	164,81	ми	e	E3	-12
4	174,61	фа	f	F3	-11
5	196,00	соль	g	G3	-9
6	220,00	ля	a	A3	-7
7	246,94	си	h	B3	-5

Первая октава

Включает звуки с частотами от 261,63 Гц (включительно) до 523,25 Гц. Наименования ступеней записываются с маленькой буквы, справа сверху пишется цифра 1 (или один штрих). В научной нотации имеет номер 4.

Номер ступени	Частота, Гц	Слоговое обозначения по Гельмгольцу	Буквенное обозначение по Гельмгольцу	Американская нотация	Координатно-частотная нотация
1	261,63	до¹	c¹	C4	-4
2	293,67	ре¹	d¹	D4	-2
3	329,63	ми¹	e¹	E4	-0
4	349,23	фа¹	f¹	F4	+0
5	392,00	соль¹	g¹	G4	+2
6	440,00	ля¹	a¹	A4	+4
7	493,88	си¹	h¹	B4	+6

Вторая октава

Включает звуки с частотами от 523,25 Гц (включительно) до 1046,5 Гц. Наименования ступеней записываются с маленькой буквы, справа сверху пишется цифра 2 (или два штриха). В научной нотации имеет номер 5.

Номер ступени	Частота, Гц	Слоговое обозначения по Гельмгольцу	Буквенное обозначение по Гельмгольцу	Американская нотация	Координатно-частотная нотация
1	523,25	до²	c²	C5	+7
2	587,33	ре²	d²	D5	+9
3	659,26	ми²	e²	E5	+11
4	698,46	фа²	f²	F5	+12
5	783,99	соль²	g²	G5	+14
6	880,00	ля²	a²	A5	+16
7	987,77	си²	h²	B5	+18

Третья октава

Включает звуки с частотами от 1046,5 Гц (включительно) до 2093,0 Гц. Наименования ступеней записываются с маленькой буквы, справа сверху пишется цифра 3 (или три штриха). В научной нотации имеет номер 6.

Номер ступени	Частота, Гц	Слоговое обозначения по Гельмгольцу	Буквенное обозначение по Гельмгольцу	Американская нотация	Координатно-частотная нотация
1	1046,5	до³	c³	C6	+19
2	1174,7	ре³	d³	D6	+21
3	1318,5	ми³	e³	E6	+23
4	1396,9	фа³	f³	F6	+24
5	1568,0	соль³	g³	G6	+26
6	1760,0	ля³	a³	A6	+28
7	1975,5	си³	h³	B6	+30

Четвёртая октава

Включает звуки с частотами от 2093,0 Гц (включительно) до 4186,0 Гц. Наименования ступеней записываются с маленькой буквы, справа сверху пишется цифра 4 (или четыре штриха). В научной нотации имеет номер 7.

Номер ступени	Частота, Гц	Слоговое обозначения по Гельмгольцу	Буквенное обозначение по Гельмгольцу	Американская нотация	Координатно-частотная нотация
1	2093,0	до⁴	c⁴	C7	+31
2	2349,3	ре⁴	d⁴	D7	+33
3	2637,0	ми⁴	e⁴	E7	+35
4	2793,8	фа⁴	f⁴	F7	+36
5	3136,0	соль⁴	g⁴	G7	+38
6	3520,0	ля⁴	a⁴	A7	+40
7	3951,1	си⁴	h⁴	B7	+42

Пятая октава

Включает звуки с частотами от 4186,0 Гц (включительно) до 8372,0 Гц. В нотации Гельмгольца наименования ступеней записываются с маленькой буквы, справа сверху пишется цифра 5 (или пять штрихов). В научной нотации имеет номер 8.

Номер ступени	Частота, Гц	Слоговое обозначения по Гельмгольцу	Буквенное обозначение по Гельмгольцу	Американская нотация	Координатно-частотная нотация
1	4186,0	до⁵	c⁵	C8	+43
2	4698,6	ре⁵	d⁵	D8	+45
3	5274,0	ми⁵	e⁵	E8	+47
4	5587,7	фа⁵	f⁵	F8	+48
5	6271,9	соль⁵	g⁵	G8	+50
6	7040,0	ля⁵	a⁵	A8	+52
7	7902,1	си⁵	h⁵	B8	+54

Варианты равномерной темперации

Наиболее общепринятой и распространённой равномерной темперацией (РТ) является 12-ступенная (именно ей соответствовала приведённая выше информация).

Однако существуют и варианты равномерной темперации с другим числом делений октавы (n). При этом формула для частот модифицируется в

f(i)=f_{0}\cdot 2^{i/n}

.

Чтобы выражение «n-ступенная РТ» писать короче, вводится сокращение «n-тРТ»^{[источник не указан 4438 дней]}, где числу n соответствует количество ступеней на октаву. Есть музыкальные произведения, написанные в 19-тРТ^[4], 24-тРТ, 31-тРТ^[5] и даже 53-тРТ^[6]. В начале XXI века П. А. Чернобривец работает над исследованием 20-ступенной равномерной темперации^[7].

Выбор значения n = 12 в качестве основного обусловлен тем, что для акустически чистого звучания многоголосных музыкальных произведений особенно важно чистое звучание квинт (как наиболее «консонансных», не считая октавы, интервалов), а в идеале соотношение частот образующих квинту нот должно равняться 3/2. При РТ «квинта» для каждого n отвечает такому числу k, что $2^{k/n}\approx 3/2$ , и перебором можно проверить, что при n = 12 (с k = 7 — это ближайшее целое к ln(3/2)/ln(2)n) достигается лучшее приближение, нежели при меньших или несколько бóльших n (точнее было бы при n = 41 или n = 53, но слишком большие n неудобны с практической точки зрения)^[8].

Равномерные темперации могут также делить иной интервал, не только октаву, на целое число равных ступеней. Чтобы избежать неясности, в англоязычной литературе, например, широко используется словосочетание «equal divisions of an octave» или его сокращённая форма EDO. В русском языке тот же смысл передаёт словосочетание «равные деления октавы» или РДО. Поэтому 12-тРТ может также обозначаться как 12РДО, 19-тРТ как 19РДО и так далее^[9].

Равномерно темперированный и другие строи

Наряду с господствующим ныне равномерно темперированным строем существовали и другие строи. Русский исследователь музыки XIX века Владимир Одоевский, например, написал так:

Русский простолюдин с музыкальным дарованием, у которого ухо ещё не испорчено ни уличными шарманками, ни итальянскою оперою, поет весьма верно; и по собственному чутью берет интервал весьма отчетливо, разумеется, не в нашей уродливой темперированной гамме <…> Я записывал с голоса [известного нашего русского певца Ивана Евстратиевича Молчанова, человека с чудною музыкальною организациею] весьма интересную песню: «У Троицы, у Сергия, было под Москвою» <…> заметил, что Si певца никак не подходит к моему фортепианному Si; и Молчанов также заметил, что здесь что-то не то <…> Это навело меня на мысль устроить фортепиано нетемперированное в такой системе, как обыкновенное. За основание я принял естественную гамму, вычисленную акустическими логарифмами по методе Прони; в этом энгармоническом клавицине все квинты чистые, диезы, отмеченные красным цветом, отделены от бемолей и по невозможности в самом механизме инструмента, я пожертвовал fa $\flat$ и ut $\flat$ , чтобы сохранить si $\sharp$ и mi $\sharp$ , потому что наши народные певцы — по непонятной для меня причине поют более в диезных нежели в бемольных тонах
— В. Ф. Одоевский^[10]

Широкомасштабное движение музыкантов-аутентистов практикует воспроизведение музыки прошлого в тех строях, в которых исполняемая ими музыка была написана.

В неевропейской традиционной музыке сохраняется практика использования строев, отличающихся от равномерно темперированного, — во всех жанрах и формах мощной макамо-мугамной традиции^[11], а также в индийской^[12] и др.

Примечания

↑ См. Werckmeister A. Musicae mathematicae hodegus curiosus… (1687), Musikalische Temperatur, oder… (1691)
↑ Bach, J. S.^[англ.]. J. S. Bach: The Well-Tempered Clavier (неопр.) / Palmer, Willard A.. — Los Angeles, CA: Alfred Music Publishing^[англ.], 2004. — С. 4. — ISBN 0882848313.
↑ Hart R. Quantifying Ritual: Political Cosmology, Courtly Music, and Precision Mathematics in Seventeenth-Century China Архивировано 5 марта 2012 года.
↑ Nine Preludes for Two Pianos in 19-Tone Temperament Архивная копия от 26 февраля 2012 на Wayback Machine by Joel Mandelbaum^[англ.]
↑ Concert No. 2 for two violins and orchestra Архивная копия от 1 сентября 2012 на Wayback Machine by Henk Badings^[англ.]^*, 1969
↑ Letter from B. Cicovacki to P. Scaruffi Архивная копия от 14 декабря 2011 на Wayback Machine (англ.):
… Иосип Славенски написал произведение для электронных инструментов с названием «Музыка в Натуральной тональной системе» (1937). В нём две части, первая написана для фисгармонии Бозанкета с 53 тонами в октаве…"

(«…JOSIP STOLCER SLAVENSKI <…> composed a composition for electronic insruments with the title Music in the Natural Tonal System (1937). It includes two movements: the first movement is written for the Bosanquet enharmonium with 53 tones in an octave»)
↑ Чернобривец П. А. Звуковысотные отношения и особенности системообразования в условиях двадцатитоновой равномерной темперации. Журнал Общества теории музыки. № 8. 2014/4. (неопр.) Дата обращения: 29 июля 2022. Архивировано 3 марта 2022 года.
↑ Волошинов, А. В. Математика и искусство (гл. 9: «Алгебра гармонии – темперация») (рус.). — Москва: Просвещение, 1992. — ISBN 5090027056. Архивировано 8 января 2019 года.
↑ Алиева И. Микротональная нотация посредством числовых уточнений знаков альтерации (на примере звукоряда тара) Архивная копия от 15 января 2013 на Wayback Machine
↑ Одоевский В. Ф. [«Русскии простолюдин...»]. Цит. из сборника В. Ф. Одоевский. Музыкально-литературное наследие.— М.: Государственное музыкальное издательство, 1956.— с. 481—482
↑ В отечественной науке на это указывал, начиная с конца 1920-х годов, выдающийся музыковед и этнограф В. М. Беляев; см. например, его работы: Туркменская музыка. Том 1. М., 1928 (совм. с В. А. Успенским); Руководство для обмера народных музыкальных инструментов, М., 1931; Музыкальные инструменты Узбекистана, М., 1933; Ладовые системы в музыке народов СССР // В. М. Беляев. [Сб. статей]. М.: Сов. композитор, 1990. Среди современных публикаций — доклад С. Агаевой и Ш. Гаджиева «О проблемах исследования звуковысотной системы азербайджанских мугамов». VII Междунар. симпозиум науч.-иссл. группы «Макам» при Междунар. Совете по трад. муз. ЮНЕСКО. Баку. 2011. С. 20-32; см. также упомянутую статью Архивная копия от 15 января 2013 на Wayback Machine И. Алиевой. Краткий обзор и библиографию зарубежной литературы по данной тематике см. в O. Wright et al. Arab Music. I. Art Music // The New Grove Dictionary of Music and Musicians. London, New York, 2001; H. Farhat. Iran. II. Classical traditions. 2. Theory of intervals and scales, 3. The modal system. // ibid. Также см. 'Issam El-Mallah. Arab Music and Musical Notation. Hans Schneider Verlag. Tutzing. 2001; S. Marcus. The Interface between Theory and Practice: Intonation in Arab Music. Asian Music, Vol. 24, No. 2 (1993), pp. 39-58; H. Farhat. Scales and Intervals: Theory and Practice, Irish Musical Studies, i (1990), pp. 216-26.
↑ Краткий обзор и библиографию зарубежной литературы по данной тематике см. в Powers H. and Widdess R. India, subcontinent of. III. Theory and practice of classical music. 1. Tonal systems // The New Grove Dictionary of Music and Musicians. London, New York, 2001.

Литература

Barbour J. M. Tuning and temperament: A historical survey. East Lansing, 1951; Mineola, 2004;
Lindley M. Lutes, viols and temperaments. Cambridge, 1984;
Lindley M. Stimmung und Temperatur // Geschichte der Musiktheorie. Bd. 6. Darmstadt, 1987, S.109-331.
Lindley M., Turner-Smith R. Mathematical models of musical scales: A new approach. Bonn, 1993;
Auhagen W. Stimmung und Temperatur // Die Musik in Geschichte und Gegenwart. Sachteil. Bd. 8. Kassel; Basel, 1998, Sp. 1831—1847.
Rasch R. Tuning and temperament // The Cambridge history of Western music theory. Cambridge, 2002, p.193-222.

Ссылки

Зубов А. Ю. Темперация // Большая российская энциклопедия. Т. 32. М., 2016, с. 27

[1] См. Werckmeister A. Musicae mathematicae hodegus curiosus… (1687), Musikalische Temperatur, oder… (1691)

[alfred-2] Bach, J. S.^[англ.]. J. S. Bach: The Well-Tempered Clavier (неопр.) / Palmer, Willard A.. — Los Angeles, CA: Alfred Music Publishing^[англ.], 2004. — С. 4. — ISBN 0882848313.

[3] Hart R. Quantifying Ritual: Political Cosmology, Courtly Music, and Precision Mathematics in Seventeenth-Century China Архивировано 5 марта 2012 года.

[4] Nine Preludes for Two Pianos in 19-Tone Temperament Архивная копия от 26 февраля 2012 на Wayback Machine by Joel Mandelbaum^[англ.]

[5] Concert No. 2 for two violins and orchestra Архивная копия от 1 сентября 2012 на Wayback Machine by Henk Badings^[англ.]^*, 1969

[6] Letter from B. Cicovacki to P. Scaruffi Архивная копия от 14 декабря 2011 на Wayback Machine (англ.):
… Иосип Славенски написал произведение для электронных инструментов с названием «Музыка в Натуральной тональной системе» (1937). В нём две части, первая написана для фисгармонии Бозанкета с 53 тонами в октаве…"

(«…JOSIP STOLCER SLAVENSKI <…> composed a composition for electronic insruments with the title Music in the Natural Tonal System (1937). It includes two movements: the first movement is written for the Bosanquet enharmonium with 53 tones in an octave»)

[7] Чернобривец П. А. Звуковысотные отношения и особенности системообразования в условиях двадцатитоновой равномерной темперации. Журнал Общества теории музыки. № 8. 2014/4. (неопр.) Дата обращения: 29 июля 2022. Архивировано 3 марта 2022 года.

[volosh-8] Волошинов, А. В. Математика и искусство (гл. 9: «Алгебра гармонии – темперация») (рус.). — Москва: Просвещение, 1992. — ISBN 5090027056. Архивировано 8 января 2019 года.

[9] Алиева И. Микротональная нотация посредством числовых уточнений знаков альтерации (на примере звукоряда тара) Архивная копия от 15 января 2013 на Wayback Machine

[10] Одоевский В. Ф. [«Русскии простолюдин...»]. Цит. из сборника В. Ф. Одоевский. Музыкально-литературное наследие.— М.: Государственное музыкальное издательство, 1956.— с. 481—482

[11] В отечественной науке на это указывал, начиная с конца 1920-х годов, выдающийся музыковед и этнограф В. М. Беляев; см. например, его работы: Туркменская музыка. Том 1. М., 1928 (совм. с В. А. Успенским); Руководство для обмера народных музыкальных инструментов, М., 1931; Музыкальные инструменты Узбекистана, М., 1933; Ладовые системы в музыке народов СССР // В. М. Беляев. [Сб. статей]. М.: Сов. композитор, 1990. Среди современных публикаций — доклад С. Агаевой и Ш. Гаджиева «О проблемах исследования звуковысотной системы азербайджанских мугамов». VII Междунар. симпозиум науч.-иссл. группы «Макам» при Междунар. Совете по трад. муз. ЮНЕСКО. Баку. 2011. С. 20-32; см. также упомянутую статью Архивная копия от 15 января 2013 на Wayback Machine И. Алиевой. Краткий обзор и библиографию зарубежной литературы по данной тематике см. в O. Wright et al. Arab Music. I. Art Music // The New Grove Dictionary of Music and Musicians. London, New York, 2001; H. Farhat. Iran. II. Classical traditions. 2. Theory of intervals and scales, 3. The modal system. // ibid. Также см. 'Issam El-Mallah. Arab Music and Musical Notation. Hans Schneider Verlag. Tutzing. 2001; S. Marcus. The Interface between Theory and Practice: Intonation in Arab Music. Asian Music, Vol. 24, No. 2 (1993), pp. 39-58; H. Farhat. Scales and Intervals: Theory and Practice, Irish Musical Studies, i (1990), pp. 216-26.

[12] Краткий обзор и библиографию зарубежной литературы по данной тематике см. в Powers H. and Widdess R. India, subcontinent of. III. Theory and practice of classical music. 1. Tonal systems // The New Grove Dictionary of Music and Musicians. London, New York, 2001.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

Равномерно темперированный строй

Содержание

Исторический очерк

Вычисление частот звуков

Сравнение с натуральным строем