Касательная прямая

График функции (чёрная кривая) и касательная прямая (красная прямая)

Каса́тельная пряма́я — прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.

Строгое определение

• Пусть функция $f\colon U(x_{0})\subset \mathbb {R} \to \mathbb {R}$ определена в некоторой окрестности точки $x_{0}\in \mathbb {R}$, и дифференцируема в ней: $f\in {\mathcal {D}}(x_{0})$. Касательной прямой к графику функции $f$ в точке $x_{0}$ называется график линейной функции, задаваемой уравнением

  $y=f(x_{0})+f'(x_{0})(x-x_{0}),\quad x\in \mathbb {R}$.

• Если функция $f$ имеет в точке $x_{0}$ бесконечную производную $f'(x_{0})=\pm \infty ,$ то касательной прямой в этой точке называется вертикальная прямая, задаваемая уравнением

  $x=x_{0}.$

Замечание

Прямо из определения следует, что график касательной прямой проходит через точку $(x_{0},f(x_{0}))$. Угол $\alpha$ между касательной к кривой и осью Ох удовлетворяет уравнению

$\operatorname {tg} \,\alpha =f'(x_{0})=k,$

где $\operatorname {tg}$ обозначает тангенс, а $\operatorname {k}$ — коэффициент наклона касательной. Производная в точке $x_{0}$ равна угловому коэффициенту касательной к графику функции $y=f(x)$ в этой точке.

Касательная как предельное положение секущей

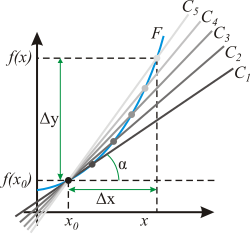
Пусть $f\colon U(x_{0})\to \mathbb {R}$ и $x_{1}\in U(x_{0}).$ Тогда прямая линия, проходящая через точки $(x_{0},f(x_{0}))$ и $(x_{1},f(x_{1}))$ задаётся уравнением

$y=f(x_{0})+{\frac {f(x_{1})-f(x_{0})}{x_{1}-x_{0}}}(x-x_{0}).$

Эта прямая проходит через точку $(x_{0},f(x_{0}))$ для любого $x_{1}\in U(x_{0}),$ и её угол наклона $\alpha (x_{1})$ удовлетворяет уравнению

$\operatorname {tg} \,\alpha (x_{1})={\frac {f(x_{1})-f(x_{0})}{x_{1}-x_{0}}}.$

В силу существования производной функции $f$ в точке $x_{0},$ переходя к пределу при $x_{1}\to x_{0},$ получаем, что существует предел

$\lim \limits _{x_{1}\to x_{0}}\operatorname {tg} \,\alpha (x_{1})=f'(x_{0}),$

а в силу непрерывности арктангенса и предельный угол

$\alpha =\operatorname {arctg} \,f'(x_{0}).$

Прямая, проходящая через точку $(x_{0},f(x_{0}))$ и имеющая предельный угол наклона, удовлетворяющий $\operatorname {tg} \,\alpha =f'(x_{0}),$ задаётся уравнением касательной:

$y=f(x_{0})+f'(x_{0})(x-x_{0}).$

Касательная к окружности

Отрезки касательных

Прямая, имеющая одну общую точку с окружностью и лежащая с ней в одной плоскости, называется касательной к окружности.

Свойства

1. Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
2. Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
3. Длина отрезка касательной, проведённой к окружности единичного радиуса, взятого между точкой касания и точкой пересечения касательной с радиусом, является тангенсом угла между этим радиусом и направлением от центра окружности на точку касания. «Тангенс» от лат. tangens — «касательная».

Вариации и обобщения

Односторонние полукасательные

• Если существует правая производная $f'_{+}(x_{0})<\infty ,$ то пра́вой полукаса́тельной к графику функции $f$ в точке $x_{0}$ называется луч

$y=f(x_{0})+f'_{+}(x_{0})(x-x_{0}),\quad x\geqslant x_{0}.$

• Если существует левая производная $f'_{-}(x_{0})<\infty ,$ то ле́вой полукаса́тельной к графику функции $f$ в точке $x_{0}$ называется луч

$y=f(x_{0})+f'_{-}(x_{0})(x-x_{0}),\quad x\leqslant x_{0}.$

• Если существует бесконечная правая производная $f'_{+}(x_{0})=+\infty \;(-\infty ),$ то правой полукасательной к графику функции $f$ в точке $x_{0}$ называется луч

$x=x_{0},\;y\geqslant f(x_{0})\;(y\leqslant f(x_{0})).$

• Если существует бесконечная левая производная $f'_{-}(x_{0})=+\infty \;(-\infty ),$ то правой полукасательной к графику функции $f$ в точке $x_{0}$ называется луч

$x=x_{0},\;y\leqslant f(x_{0})\;(y\geqslant f(x_{0})).$

См. также

• Дифференцируемая функция
• Касательное пространство
• Нормаль, бинормаль
• Теорема о секущих