Электростатическое поле

Электростати́ческое по́ле — поле, созданное неподвижными в пространстве и неизменными во времени электрическими зарядами. Оно представляет собой особый вид материи, связанный с электрическими зарядами и передающий действия зарядов друг на друга^[1].

Является частным случаем электрического поля (последнее может быть переменным во времени, а также, помимо зарядов, может порождаться переменным магнитным полем). Регистрируется через силу, действующую на неподвижный пробный точечный заряд, помещённый в изучаемую точку пространства; этот пробный заряд должен быть малым, чтобы не повлиять на свойства электростатического поля.

Основные характеристики электростатического поля ( $\mathbf {r}$ — радиус-вектор):

напряжённость $\mathbf {E} (\mathbf {r} )$ ;
потенциал $\varphi (\mathbf {r} )$ .

Электростатическое поле обладает свойством потенциальности, то есть работа поля по перемещению в нём заряда зависит только от начального и конечного положений этого заряда, но не от вида траектории.

Электростатическое поле заданного распределения зарядов может быть рассчитано на основе закона Кулона или посредством решения уравнения Пуассона с граничными условиями.

Силовые линии электростатического поля всегда незамкнуты: начинаются на положительных зарядах (или же на бесконечности) и заканчиваются на отрицательных зарядах (или на бесконечности). При этом, как и силовые линии других векторных полей, они не пересекаются и не касаются друг друга, а густота их тем больше, чем больше напряжённость поля в данном месте.

Аналогом электростатического поля, в плане математического описания, во многом является гравитационное поле, для которого логическую роль закона Кулона перенимает закон всемирного тяготения, а вместо точечного заряда рассматривается точечная масса. Но гравитационная сила, в отличие от электростатической, всегда является силой притяжения.

Описание. Фундаментальные формулы

Электростатическое поле описывается напряжённостью ( $\mathbf {E}$ , размерность В/м) или потенциалом ( $\varphi$ , Вольт). Чаще всего ставится задача найти распределение поля/потенциала во всём пространстве по заданному распределению сторонних (то есть «привнесённых» постановщиком задачи) зарядов или по известным условиям на потенциалы задействованных проводников. Из-за сторонних зарядов могут изменяться положения существующих в средах «своих» зарядов, которые становятся дополнительными источниками поля. Математический аппарат для расчетов представляется ниже, хотя некоторые сравнительно простые задачи допускают решение и без него (угадыванием, из соображений симметрии, на основе формулы Кулона для случая вакуума и пр.). Ниже все соотношения будут приведены в системе СИ.

Уравнения Максвелла

Основными формулами электростатики являются два из четырёх уравнений Максвелла, которые могут быть записаны в дифференциальной

\nabla \cdot \mathbf {D} =\rho \qquad \nabla \times \mathbf {E} =0

либо интегральной

\oint \limits _{\mathbf {s} }\mathbf {D} \cdot d\mathbf {s} =Q\qquad \oint \limits _{\mathbf {l} }\mathbf {E} \cdot d\mathbf {l} =0

формах. Здесь $\mathbf {E}$ — напряженность электрического поля, $\mathbf {D}$ — вектор электрического смещения, $\nabla$ — оператор набла, $\rho$ — объёмная плотность заряда. Интегрирование производится по выбранной замкнутой поверхности или замкнутому контуру, через $Q$ обозначен суммарный заряд внутри поверхности.

Физический смысл соотношений: электростатическое поле создаётся зарядами и всегда является безвихревым (потенциальным).

Уравнение Пуассона

В электростатике вводится скалярный потенциал электрического поля, связанный с напряжённостью поля как

\mathbf {E} =-\nabla \varphi

.

Для $\varphi$ существует уравнение Пуассона, при $\mathbf {D} =\varepsilon _{0}\varepsilon \mathbf {E}$ записывающееся как

\varepsilon _{0}\nabla \cdot \left(\varepsilon \nabla \varphi \right)=-\rho

,

которое для случая однородного (то есть с координатно-независимой проницаемостью $\varepsilon$ ) диэлектрика обретает вид

\Delta \varphi =-{\frac {\rho }{\varepsilon _{0}\varepsilon }}

,

а при отсутствии заряда в некоторой области превращается в ней в уравнение Лапласа. Уравнение Пуассона (или Лапласа) является основой для численных расчётов электрического поля. В последнем выражении $\Delta$ — оператор Лапласа. Символ ε₀ — электрическая постоянная (также известная как «абсолютная диэлектрическая проницаемость свободного пространства») с единицами измерения C ² м ⁻² Н ⁻¹.

Принцип суперпозиции

Ввиду линейности уравнений Максвелла электрические поля удовлетворяют принципу суперпозиции, который гласит, что полное электрическое поле в точке от распределённых в пространстве зарядов равно векторной сумме электрических полей, создаваемых в этой точке отдельными зарядами:

{\boldsymbol {E}}({\boldsymbol {r}})={\boldsymbol {E}}_{1}({\boldsymbol {r}})+{\boldsymbol {E}}_{2}({\boldsymbol {r}})+{\boldsymbol {E}}_{3}({\boldsymbol {r}})+\cdots

.

Этот принцип полезен при расчёте поля, создаваемого множественными зарядами. Исключение из принципа суперпозиции возникает для случая сред с зависящей от поля проницаемостью ( $\varepsilon =\varepsilon (|\mathbf {E} |)$ ), в первую очередь характерной для сегнетоэлектриков.

Случай однородного поля

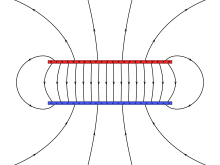
Электрическое поле называют однородным, если вектор его напряжённости одинаков во всех точках рассматриваемой области. Такой случай является наиболее простым.

Однородное поле создаёт равномерно заряженная плоскость или любая комбинация равномерно заряженных плоскопараллельных слоёв. Самым важным примером является плоский конденсатор — две разноимённо заряженные параллельные пластины большой площади, пространство между которыми заполнено однородным диэлектрическим материалом.

С точностью до краевых эффектов, электрическое поле между пластинами однородно и по величине составляет

|\mathbf {E} |={\frac {|\sigma |}{\varepsilon _{0}\varepsilon }}={\frac {|U|}{d}}

,

где $\sigma$ — поверхностная плотность заряда каждой из пластин, $U$ — приложенное между пластинами напряжение (разность потенциалов), $d$ — расстояние между пластинами.

Картина силовых линий для описанного случая представлена на рисунке.

Закон Кулона

Поле одного точечного заряда

В случае вакуума или однородного диэлектрика с проницаемостью $\varepsilon =\,$ const поле точечного заряда может быть найдено с помощью закона Кулона, который гласит, что частица с электрическим зарядом $q_{1}$ в точке ${\boldsymbol {r}}_{1}$ (радиус-вектор) действует на частицу с зарядом $q\,$ в точке ${\boldsymbol {r}}$ с силой :^[2]

{\boldsymbol {F}}={1 \over 4\pi \varepsilon _{0}\varepsilon }{\frac {q_{1}q}{|{\boldsymbol {r}}-{\boldsymbol {r}}_{1}|^{2}}}{\hat {\boldsymbol {r}}}_{1,q}={1 \over 4\pi \varepsilon _{0}\varepsilon }{\frac {q_{1}q({\boldsymbol {r}}-{\boldsymbol {r}}_{1})}{|{\boldsymbol {r}}-{\boldsymbol {r}}_{1}|^{3}}}

,

где ${\hat {\boldsymbol {r}}}_{1,q}$ — единичный вектор в направлении от точки ${\boldsymbol {r}}_{1}$ в точку ${\boldsymbol {r}}$ .

Когда заряды $q$ и $q_{1}$ имеют одинаковые знаки, эта сила положительна, то есть частицы отталкиваются друг от друга. Когда заряды имеют разные знаки, сила отрицательна, что указывает на притяжение частиц. Чтобы упростить расчёт кулоновской силы для любого заряда в точке ${\boldsymbol {r}}$ , это выражение можно разделить на $q$ , оставив выражение, которое зависит только от заряда источника^[3]

{\boldsymbol {E}}({\boldsymbol {r}})={1 \over 4\pi \varepsilon _{0}\varepsilon }{\frac {q_{1}({\boldsymbol {r}}-{\boldsymbol {r}}_{1})}{|{\boldsymbol {r}}-{\boldsymbol {r}}_{1}|^{3}}}

Это электрическое поле в точке ${\boldsymbol {r}}$ , создаваемое точечным зарядом $q_{1}$ . Оно представляет собой векторную функцую, которая равна кулоновской силе на единицу заряда, испытываемой положительным точечным зарядом в точке ${\boldsymbol {r}}$ . Поскольку формула даёт величину и направление электрического поля в любой точке ${\boldsymbol {r}}$ пространства (кроме места нахождения самого заряда, ${\boldsymbol {r}}_{1}$ , где оно бесконечно), ею определяется векторное поле.

Кулоновская сила действующая на заряд величиной $q$ , в любой точке пространства равна произведению заряда и электрического поля в этой точке:

{\boldsymbol {F}}=q{\boldsymbol {E}}

.

Закон Кулона имеет обобщения на случаи нескольких точечных зарядов или распределённого в пространстве заряда.

Поле нескольких точечных зарядов

Если заряды $q_{1},q_{2},...,q_{n}$ неподвижно расположены в точках $\mathbf {r} _{1},\mathbf {r} _{2},...\mathbf {r} _{n}$ , то из принципа суперпозиции следует, что результирующее поле будет суммой полей, создаваемых индивидуально каждой частицей и описываемых законом Кулона, а именно:

{\boldsymbol {E}}({\boldsymbol {r}})={1 \over 4\pi \varepsilon _{0}\varepsilon }{\frac {q_{1}({\boldsymbol {r}}-{\boldsymbol {r}}_{1})}{|{\boldsymbol {r}}-{\boldsymbol {r}}_{1}|^{3}}}+{1 \over 4\pi \varepsilon _{0}\varepsilon }{\frac {q_{2}({\boldsymbol {r}}-{\boldsymbol {r}}_{2})}{|{\boldsymbol {r}}-{\boldsymbol {r}}_{2}|^{3}}}+\cdots ={1 \over 4\pi \varepsilon _{0}\varepsilon }\sum _{k=1}^{n}{\frac {q_{k}({\boldsymbol {r}}-{\boldsymbol {r}}_{k})}{|{\boldsymbol {r}}-{\boldsymbol {r}}_{k}|^{3}}}

.

Непрерывное распределение заряда

Принцип суперпозиции позволяет рассчитать электрическое поле от непрерывного распределения заряда $\rho ({\boldsymbol {r}})$ (где $\rho$ — плотность заряда в кулонах на кубический метр). Учитывая заряд $\rho ({\boldsymbol {r}}')dV$ в каждом небольшом объёме пространства $dV$ в точке ${\boldsymbol {r}}'$ в виде точечного заряда, электрическое поле $d{\boldsymbol {E}}({\boldsymbol {r}})$ в точке ${\boldsymbol {r}}$ можно рассчитать как

d{\boldsymbol {E}}({\boldsymbol {r}})={1 \over 4\pi \varepsilon _{0}\varepsilon }{\rho ({\boldsymbol {r}}')({\boldsymbol {r}}-{\boldsymbol {r}}')dV \over |{\boldsymbol {r}}-{\boldsymbol {r}}'|^{3}}

.

Полное электрическое поле находится путем «сложения» вкладов от всех малых объёмов путем интегрирования по объёму распределения заряда $\rho (r')$ :

{\boldsymbol {E}}({\boldsymbol {r}})={1 \over 4\pi \varepsilon _{0}\varepsilon }\iiint \limits _{V}\,{\rho ({\boldsymbol {r}}')({\boldsymbol {r}}-{\boldsymbol {r}}')dV \over |{\boldsymbol {r}}-{\boldsymbol {r}}'|^{3}}

.

Аналогичные уравнения записываются для поверхностного заряда с непрерывным распределением $\sigma ({\boldsymbol {r}})$ где $\sigma$ — плотность заряда в кулонах на квадратный метр, а также для линейных зарядов с распределением $\lambda ({\boldsymbol {r}})$ где $\lambda$ — плотность заряда в кулонах на метр:

{\boldsymbol {E}}({\boldsymbol {r}})={1 \over 4\pi \varepsilon _{0}\varepsilon }\iint \limits _{S}\,{\sigma ({\boldsymbol {r}}')({\boldsymbol {r}}-{\boldsymbol {r}}')dA \over |{\boldsymbol {r}}-{\boldsymbol {r}}'|^{3}},\qquad {\boldsymbol {E}}({\boldsymbol {r}})={1 \over 4\pi \varepsilon _{0}\varepsilon }\int \limits _{P}\,{\lambda ({\boldsymbol {r}}')({\boldsymbol {r}}-{\boldsymbol {r}}')dL \over |{\boldsymbol {r}}-{\boldsymbol {r}}'|^{3}}

.

Параллели c гравитационным полем

Закон Кулона, описывающий взаимодействие электрических зарядов в вакууме

\mathbf {F} =q\left({\frac {Q}{4\pi \varepsilon _{0}}}{\frac {\mathbf {\mathbf {r} } }{|\mathbf {r} |^{3}}}\right)=q\mathbf {E}

,

похож на закон всемирного тяготения Ньютона

\mathbf {F} =m\left(-GM{\frac {\mathbf {\mathbf {r} } }{|\mathbf {r} |^{3}}}\right)=m\mathbf {g}

(здесь предполагается, что создающие поле заряд $Q$ или масса $M$ помещены в начало координат, а $\mathbf {r/|r|}$ — единичный вектор в направлении к пробному заряду $q$ или пробной массе $m$ ), что указывает на логическое сходство между электрическим полем E и гравитационным полем g или связанными с ними потенциалами. Масса иногда называется «гравитационным зарядом».^[4] В последней формуле $G$ — гравитационная постоянная. И электростатические, и гравитационные силы являются центральными, консервативными и подчиняются закону обратных квадратов.

Различие состоит в нереализуемости случая отталкивания для гравитации, который возможен для зарядов одинаковых знаков в электростатике. При этом электростатическому притяжению соответствует как раз различие знаков зарядов (эта неодинаковость отражена наличием знака минус в выражении для ньютоновской силы).

Электростатическое поле в средах

Характер реакции материальной среды на наложение электрического поля (будь то электростатическое или изменяющееся со временем) зависит от того, насколько свободными являются электрические заряды (ионы, электроны, дырки) этой среды.

Если они могут свободно перемещаться, то на поверхности возникает индуцированный заряд, распределённый таким образом, чтобы воспрепятствовать проникновению поля вглубь среды — такой вариант реакции типичен для проводящих металлических материалов. У границы вакуум—металл элекростатическое поле присутствует только со стороны вакуума и содержит только нормальную (перпендикулярную) к границе компоненту: $\mathbf {E} =\mathbf {E} _{n}$ (см. рис.).

Если заряды свободно перемещаться не могут, происходит их локальное, на атомных масштабах, смещение, в результате чего в местах неоднородностей материала и на границах появляется связанный заряд — такой отклик характерен для диэлектриков (см. в статье Диэлектрическая проницаемость). На границе диэлектрик—диэлектрик могут присутствовать и нормальная ( $\mathbf {E} _{n}$ ), и тангенциальная ((параллельная границе, $\mathbf {E} _{\tau }$ ) компоненты, причём на границе без стороннего заряда должны сохранять непрерывность величины $\mathbf {E} _{\tau }$ и $\varepsilon \mathbf {E} _{n}$ .

В полупроводниках возможна «смешанная» реакция.

Перемещённые электрические заряды сами становятся источниками поля, искажая картину поля не только непосредственно в среде, но и во всём пространстве (например, вне куска диэлектрика). Поэтому электрическое поле не может быть сначала рассчитано без диэлектриков, а затем снижено в $\varepsilon (\mathbf {r} )$ раз там, где диэлектрик наличествует. Подобный подход в виде исключения допустим для некоторых простейших геометрий (среди которых случай точечного заряда, окружённого сферически симметричным диэлектриком, проницаемость которого зависит только от удаления от центра).

См. также

Примечания

↑ Энциклопедический словарь юного физика. — Москва: Педагогика, 1984. — 352 с. с. — ISBN Э4306000000-079/005(01)-84 56 - 84.
↑ Purcell, p7: "… the interaction between electric charges at rest is described by Coulomb’s Law: two stationary electric charges repel or attract each other with a force proportional to the product of the magnitude of the charges and inversely proportional to the square of the distance between them.
↑ Purcell, Edward. Electricity and Magnetism, 2nd Ed.. — Cambridge University Press, 2011. — P. 8–9. — ISBN 978-1139503556.
↑ Salam, Abdus (16 December 1976). "Quarks and leptons come out to play". New Scientist. 72.

[1] Энциклопедический словарь юного физика. — Москва: Педагогика, 1984. — 352 с. с. — ISBN Э4306000000-079/005(01)-84 56 - 84.

[2] Purcell, p7: "… the interaction between electric charges at rest is described by Coulomb’s Law: two stationary electric charges repel or attract each other with a force proportional to the product of the magnitude of the charges and inversely proportional to the square of the distance between them.

[Purcell-3] Purcell, Edward. Electricity and Magnetism, 2nd Ed.. — Cambridge University Press, 2011. — P. 8–9. — ISBN 978-1139503556.

[4] Salam, Abdus (16 December 1976). "Quarks and leptons come out to play". New Scientist. 72.

[1]

[2]

[3]

[4]

Электростатическое поле

Содержание