Цилиндрические параболические координаты
Перейти к навигации
Перейти к поиску
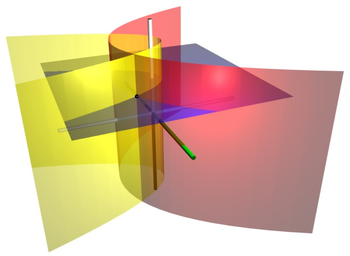
Цилиндрические параболические координаты (координаты параболического цилиндра) — система координат, обобщающая параболические координаты на трёхмерный случай путём добавления третьей (декартовой) координаты , то есть аппликаты.
Существует несколько вариантов ориентации этих координат. Наиболее распространённой является ориентация, соответствующая
где — размерный множитель.
Поверхности уровня и суть параболические цилиндры, образующие которых параллельны оси .
Связь с другими системами координат[править | править код]
Прямоугольная система координат [править | править код]
Цилиндрическая система координат [править | править код]
Коэффициенты Ламе[править | править код]
Коэффициенты Ламе в данных координатах имеют следующий вид:
Выражение основных дифференциальных операторов[править | править код]
Градиент[править | править код]
Дивергенция[править | править код]
Ротор[править | править код]
Лапласиан[править | править код]
См. также[править | править код]
- Прямоугольная (Декартова) система координат
- Аффинная (косоугольная) система координат
- Координаты Риндлера — в пространстве Минковского
- Барицентрические координаты
- Биангулярные координаты
- Полярная система координат
- Цилиндрическая система координат
- Сферическая система координат
- Тороидальная система координат
- Цилиндрические параболические координаты
- Параболические координаты
- Бицентрические координаты
- Биполярные координаты
- Бицилиндрические координаты
- Биангулярные координаты
- Трилинейные координаты
- Проективные координаты
- Эллипсоидальные координаты (эллиптические координаты)
- Конические координаты
Ссылки[править | править код]
- Weisstein, Eric W. Parabolic Cylindrical Coordinates (англ.) на сайте Wolfram MathWorld.
Для улучшения этой статьи желательно:
|












![{\displaystyle \mathrm {div} {\vec {A}}(u,\;v,\;z)={\frac {1}{c(u^{2}+v^{2})}}\left[{\frac {\partial }{\partial u}}\left({\sqrt {u^{2}+v^{2}}}A_{u}\right)+{\frac {\partial }{\partial v}}\left({\sqrt {u^{2}+v^{2}}}A_{v}\right)\right]+{\frac {\partial A_{z}}{\partial z}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57deaef6a58d441691d307f091d7d923e9afc9c2)
![{\displaystyle \mathrm {rot} \,{\vec {A}}={\frac {1}{c{\sqrt {u^{2}+v^{2}}}}}\left[{\frac {\partial }{\partial v}}A_{z}-{\frac {\partial }{\partial z}}(c{\sqrt {u^{2}+v^{2}}}A_{v})\right]{\vec {e}}_{u}+{\frac {1}{c{\sqrt {u^{2}+v^{2}}}}}\left[{\frac {\partial }{\partial z}}(c{\sqrt {u^{2}+v^{2}}}A_{u})-{\frac {\partial }{\partial u}}A_{z}\right]{\vec {e}}_{v}+}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcd50f8c81a8df2c284fad6084e82d7266c58f73)
![{\displaystyle +{\frac {1}{c(u^{2}+v^{2})}}\left[{\frac {\partial }{\partial u}}(c{\sqrt {u^{2}+v^{2}}}A_{v})-{\frac {\partial }{\partial v}}(c{\sqrt {u^{2}+v^{2}}}A_{u})\right]{\vec {e}}_{z}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5417e6775a7bb1febc07b1e3f4eca97a5a1874)
![{\displaystyle \Delta F(u,\;v,\;z)={\frac {1}{c^{2}(u^{2}+v^{2})}}\left[{\frac {\partial ^{2}F}{\partial u^{2}}}+{\frac {\partial ^{2}F}{\partial v^{2}}}\right]+{\frac {\partial ^{2}F}{\partial z^{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b25a03f2376fbe7965926a6be4e9b70f737890dd)
