Метод конечных элементов

Решение методом конечных элементов двухмерной магнитостатической задачи (линии и цвет означают направление и величину магнитной индукции)

Разбиение на конечные элементы. Размер элементов можно менять, уменьшая его вблизи интересующей области, и увеличивая — для снижения затрат процессорного времени

Метод конечных элементов (МКЭ) — численный метод решения дифференциальных уравнений с частными производными, а также интегральных уравнений, возникающих при решении задач прикладной физики. Метод широко используется для решения задач механики деформируемого твёрдого тела, теплообмена, гидродинамики и электродинамики.

Идея метода

Суть метода следует из его названия. Область, в которой ищется решение дифференциальных уравнений, разбивается на конечное количество подобластей (элементов). В каждом из элементов произвольно выбирается вид аппроксимирующей функции. В простейшем случае это полином первой степени. Вне своего элемента аппроксимирующая функция равна нулю. Значения функций на границах элементов (узлах) являются решением задачи и заранее неизвестны. Коэффициенты аппроксимирующих функций обычно ищутся из условия равенства значения соседних функций на границах между элементами (в узлах). Затем эти коэффициенты выражаются через значения функций в узлах элементов. Составляется система линейных алгебраических уравнений. Количество уравнений равно количеству неизвестных значений в узлах, на которых ищется решение исходной системы, прямо пропорционально количеству элементов и ограничивается только возможностями ЭВМ. Так как каждый из элементов связан с ограниченным количеством соседних, система линейных алгебраических уравнений имеет разрежённый вид, что существенно упрощает её решение.

С точки зрения вычислительной математики, идея метода конечных элементов заключается в том, что минимизация функционала вариационной задачи осуществляется на совокупности функций, каждая из которых определена на своей подобласти, для численного анализа системы позволяет рассматривать его как одну из конкретных ветвей диакоптики — общего метода исследования систем путём их расчленения.

Иллюстрация метода на одномерном примере

Функция на $H_0^1,$ с нулевыми значениями на концах (голубая), и аппроксимация этой функции отрезками (красная).

Базисные функции v_k (голубые) и линейная комбинация из них, которая аппроксимирует искомую функцию (красная).

Визуализация деформации машины при асимметричном ударе, используя метод конечных элементов.

Пусть в одномерном пространстве Р1 необходимо решить следующее одномерное дифференциальное уравнение для нахождения функции $u$ на промежутке от 0 до 1. На границах области значение функции $u$ равно 0:

$\mbox{ P1 }:\begin{cases} u''(x)=f(x) \mbox{ in } (0,1), \\ u(0)=u(1)=0, \end{cases}$

где $f$ известная функция, $u$ неизвестная функция от $x$. $u''$ вторая производная от $u$ по $x$. Решение поставленной задачи методом конечных элементов разобьём на 2 этапа:

• Переформулируем граничную задачу в так называемую слабую (вариационную) форму. На этом этапе вычислений почти не требуется.
• На втором этапе разобьём слабую форму на конечные отрезки-элементы.

После этого возникает проблема нахождения системы линейных алгебраических уравнений, решение которой аппроксимирует искомую функцию.

Если $u$ есть решение, то для любой гладкой функции $v$, которая удовлетворяет граничным условиям $v=0$ в точках $x=0$ и $x=1$, можно записать следующее выражение:

(1) $\int_0^1 f(x)v(x) \, dx = \int_0^1 u''(x)v(x) \, dx.$

С помощью интегрирования по частям преобразуем выражение (1) к следующей форме:

(2)$\begin{align} \int_0^1 f(x)v(x) \, dx & = \int_0^1 u''(x)v(x) \, dx \\ & = u'(x)v(x)\bigg|_0^1-\int_0^1 u'(x)v'(x) \, dx \\ & = -\int_0^1 u'(x)v'(x) \, dx = -\phi (u,v). \end{align}$

Оно получено с учётом того, что $v(0)=v(1)=0$.

Разобьём область, в которой ищется решение

$u \in H_0^1$ такое, что

$\forall v \in H_0^1, \; -\phi(u,v)=\int fv$

на конечные промежутки, и получим новое пространство $V$ :

(3)$u \in V$ такое, что

$\forall v \in V, \; -\phi(u,v)=\int fv$

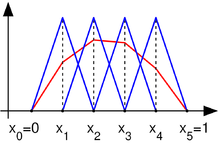
где $V$ кусочная область пространства $H_0^1$. Есть много способов для выбора функции $v$. Выбираем такую $v$, чтобы она представлялась прямыми линиями (полиномами первой степени):

$v_{k}(x)=\begin{cases} {x-x_{k-1} \over x_k\,-x_{k-1}} & \mbox{ if } x \in [x_{k-1},x_k], \\ {x_{k+1}\,-x \over x_{k+1}\,-x_k} & \mbox{ if } x \in [x_k,x_{k+1}], \\ 0 & \mbox{ otherwise},\end{cases}$

для $k=1,...,n$ (в данном примере $n=5$)

Задача преобразована.

Преимущества и недостатки

Метод конечных элементов сложнее метода конечных разностей в реализации. У МКЭ, однако, есть ряд преимуществ, проявляющихся на реальных задачах: произвольная форма обрабатываемой области; сетку можно сделать более редкой в тех местах, где особая точность не нужна.

Долгое время широкому распространению МКЭ мешало отсутствие алгоритмов автоматического разбиения области на «почти равносторонние» треугольники (погрешность, в зависимости от вариации метода, обратно пропорциональна синусу или самого острого, или самого тупого угла в разбиении). Впрочем, эту задачу удалось успешно решить (алгоритмы основаны на триангуляции Делоне), что дало возможность создавать полностью автоматические конечноэлементные САПР.

История развития метода

Возникновение метода конечных элементов связано с решением задач космических исследований в 1950-х годах. Идея МКЭ была разработана в СССР ещё в 1936 году, но из-за неразвитости вычислительной техники метод не получил развития, поэтому впервые был применён на ЭВМ лишь в 1944 году Аргирисом. Этот метод возник из строительной механики и теории упругости, а уже затем было получено его математическое обоснование. Существенный толчок в своём развитии МКЭ получил в 1963 году после того, как было доказано то, что его можно рассматривать как один из вариантов распространённого в строительной механике метода Рэлея — Ритца, который путём минимизации потенциальной энергии сводит задачу к системе линейных уравнений равновесия. После того, как была установлена связь МКЭ с процедурой минимизации, он стал применяться к задачам, описываемым уравнениями Лапласа или Пуассона. Область применения МКЭ значительно расширилась, когда было установлено (в 1968 году), что уравнения, определяющие элементы в задачах, могут быть легко получены с помощью вариантов метода взвешенных невязок, таких как метод Галёркина или метод наименьших квадратов. Это сыграло важную роль в теоретическом обосновании МКЭ, так как позволило применять его при решении многих типов дифференциальных уравнений. Таким образом, метод конечных элементов превратился в общий метод численного решения дифференциальных уравнений или систем дифференциальных уравнений.

С развитием вычислительных средств возможности метода постоянно расширяются, также расширяется и класс решаемых задач. Практически все современные расчёты на прочность проводят, используя МКЭ.

См. также

• Метод дискретного элемента
• Метод конечных разностей
• Метод конечных объёмов
• Метод подвижных клеточных автоматов

Литература

• Галлагер Р. Метод конечных элементов. Основы: Пер. с англ. — М.: Мир, 1984
• Деклу Ж. Метод конечных элементов: Пер. с франц. — М.: Мир, 1976
• Зенкевич О. Метод конечных элементов в технике — М.: Мир, 1975.
• Зенкевич О., Морган К. Конечные элементы и аппроксимация: Пер. с англ. — М.: Мир, 1986
• Сегерлинд Л. Применение метода конечных элементов — М.: Мир, 1979. — 392 С.

Ссылки

• Метод конечных элементов, В. В. Смирнов (Бийский технологический институт)
• Боровков А.И. и др. Компьютерный инжиниринг. Аналитический обзор - учебное пособие. — СПб.: Изд-во Политехн. ун-та, 2012. — 93 с. — ISBN 978-5-7422-3766-2