Непересекающиеся множества

Материал из Википедии — свободной энциклопедии
Перейти к навигации Перейти к поиску
Два непересекающихся множества.

В математике говорят, что два множества не пересекаются или дизъюнктны, если у них нет общих элементов. Эквивалентно, непересекающиеся множества — это множества, пересечение которых является пустым множеством[1]. Например, {1, 2, 3} и {4, 5, 6} непересекающиеся множества, в то время как {1, 2, 3} и {3, 4, 5} множества пересекающиеся.

Обобщения[править | править код]

Попарно независимые семейства множеств

Приведённое определение непересекающихся множеств может быть расширено на любое семейство множеств[en]*. Семейство множеств попарно дизъюнктно (элементы попарно не пересекаются), если любые два множества в семействе не имеют общих элементов[1]. Например, набор множеств { {1}, {2}, {3}, ... } попарно дизъюнктен.

Говорят, что два множества почти не пересекаются[en], если их пересечение в некотором смысле мало. Например, два бесконечных множества, пересечение которых является конечным множеством, можно считать почти не пересекающимися[2].

В топологии существуют различные обозначения разделённых множеств с более строгими условиями, чем отсутствие пересечения. Например, два множества считаются разделимыми, когда они имеют непересекающиеся замыкания или непересекающиеся окрестности. Подобно этому, в метрическом пространстве положительно разделённые множества[en] — это множества, разделённые ненулевым расстоянием[3].

Примеры[править | править код]

  • Множество, состоящее из барабана и гитары, не пересекается с множеством, состоящим из карты и книги
    Множество, состоящее из барабана и гитары, не пересекается с множеством, состоящим из карты и книги
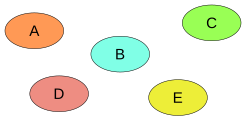
  • Семейство попарно непересекающиеся множеств
    Семейство попарно непересекающиеся множеств
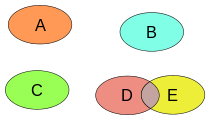
  • Семейство множеств, не являющихся попарно непересекающимися
    Семейство множеств, не являющихся попарно непересекающимися

Пересечения[править | править код]

Дизъюнктность множеств или семейств множеств можно выразить в терминах пересечений.

Два множества A и B дизъюнктны тогда и только тогда, когда их пересечение является пустым множеством[1]. Из этого определения следует, что любое множество дизъюнктно с пустым множеством и пустое множество является единственным множеством, дизъюнктным самому себе[4].

Семейство F множеств попарно дизъюнктно, если для любых двух множеств в семействе их пересечение пусто[1]. Если семейство содержит более одного множества, отсюда следует, что пересечение всех множеств семейства пусто. Однако семейство, состоящее из одного множества, по определению является «попарно дизъюнктным» и очевидно может иметь непустое пересечение. Кроме того, семейство множеств может иметь пустое пересечение, но не быть попарно дизъюнктно[5]. Например, три множества { {1, 2}, {2, 3}, {1, 3} } имеют пустое пересечение, но они не попарно дизъюнктны. Фактически нет двух дизъюнктных множеств в этом наборе. Также пустое семейство множеств является попарно дизъюнктным[6].

Семейство Хелли — это система множеств, в которой только подсемейства с пустым пересечением попарно дизъюнктны. Например, замкнутые интервалы на вещественной оси образуют семейство Хелли — если семейство замкнутых интервалов имеет пустое пересечение и минимально (то есть никакое подсемейство не имеет пустое пересечение), оно должно быть попарно дизъюнктно[7].

Дизъюнктные объединения и разбиения[править | править код]

Разбиение множества X — это любой набор взаимно дизъюнктных множеств, объединение которых равно X[8]. Любое разбиение можно эквивалентно описать отношением эквивалентности, бинарным отношением, определяющим, принадлежат два элемента одному и тому же множеству в разложении или нет[8]. Системы непересекающихся множеств[9] и измельчение разбиения[en][10] — две техники в информатике для эффективной работы с разбиениями набора объектов, соответственно, для операции объединения, которая сливает вместе два множества, и операции измельчения, которая разбивает одно множество на два.

Дизъюнктное объединение может означать две вещи. В наиболее простом случае это может означать объединение дизъюнктных множеств[11]. Но если два или более множеств не дизъюнктны, их дизъюнктное объединение может быть образовано путём модификации множеств[12][13]. Например, два множества могут быть сделаны дизъюнктыми путём замены элементов упорядоченными парами элемента и индекса, определяющего, какому множеству принадлежит элемент – первому или второму[14]. Та же техника может быть применена для семейств из более чем двух множеств[15].

См. также[править | править код]

Примечания[править | править код]

  1. ↑ 1 2 3 4 Halmos, 1960, с. 15.
  2. ↑ Halbeisen, 2011, с. 184.
  3. ↑ Copson, 1988, с. 62.
  4. ↑ Oberste-Vorth, Mouzakitis, Lawrence, 2012, с. 59.
  5. ↑ Smith, Eggen, St. Andre, 2010, с. 95.
  6. ↑ См. ответы на вопрос ″Является ли пустое семейство множеств попарно дизъюнктным?″ Архивная копия от 20 октября 2020 на Wayback Machine
  7. ↑ Bollobás, 1986, с. 82.
  8. ↑ 1 2 Halmos, 1960, с. 28.
  9. ↑ Cormen, Leiserson, Rivest, Stein, 2001, с. 498–524.
  10. ↑ Paige, Tarjan, 1987, с. 973–989.
  11. ↑ Ferland, 2008, с. 45.
  12. ↑ Arbib, Kfoury, Moll, 1981, с. 9.
  13. ↑ В книге Вавилова дизъюнктное объединение понимается только в первом смысле. Для объединения во втором смысле используется термин свободное объединение, свободная сумма или копроизведение множеств.
  14. ↑ Monin, Hinchey, 2003, с. 21.
  15. ↑ Lee, 2010, с. 64.

Литература[править | править код]

  • Ralph W. Oberste-Vorth, Aristides Mouzakitis, Bonita A. Lawrence. Bridge to Abstract Mathematics. — Mathematical Association of America, 2012. — С. 59. — (MAA textbooks). — ISBN 9780883857793.
  • P. R. Halmos. Naive Set Theory. — Springer, 1960. — С. 15. — (Undergraduate Texts in Mathematics). — ISBN 9780387900926.
  • Douglas Smith, Maurice Eggen, Richard St. Andre. A Transition to Advanced Mathematics. — 7. — Cengage Learning, 2010. — С. 95. — ISBN 978-0-495-56202-3.
  • Béla Bollobás. Combinatorics: Set Systems, Hypergraphs, Families of Vectors, and Combinatorial Probability. — Cambridge University Press, 1986. — С. 82. — ISBN 978-0-521-33703-8.
  • Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein. Chapter 21: Data structures for Disjoint Sets // Introduction to Algorithms. — 2nd. — MIT Press, 2001. — С. 498–524. — ISBN 0-262-03293-7.
  • Robert Paige, Robert E. Tarjan. Three partition refinement algorithms // SIAM Journal on Computing. — 1987. — Т. 16, вып. 6. — С. 973–989. — doi:10.1137/0216062.
  • Kevin Ferland. Discrete Mathematics: An Introduction to Proofs and Combinatorics. — Cengage Learning, 2008. — С. 45. — ISBN 9780618415380.
  • Michael A. Arbib, A. J. Kfoury, Robert N. Moll. A Basis for Theoretical Computer Science. — Springer-Verlag, 1981. — С. 9. — (The AKM series in Theoretical Computer Science: Texts and monographs in computer science). — ISBN 9783540905738.
  • Jean François Monin, Michael Gerard Hinchey. Understanding Formal Methods. — Springer, 2003. — С. 21. — ISBN 9781852332471.
  • John M. Lee. Introduction to Topological Manifolds. — 2nd. — Springer, 2010. — Т. 202. — С. 64. — (Graduate Texts in Mathematics). — ISBN 9781441979407.
  • Lorenz J. Halbeisen. Combinatorial Set Theory: With a Gentle Introduction to Forcing. — Springer, 2011. — С. 184. — (Springer monographs in mathematics). — ISBN 9781447121732.
  • Edward Thomas Copson. Metric Spaces. — Cambridge University Press, 1988. — Т. 57. — С. 62. — (Cambridge Tracts in Mathematics). — ISBN 9780521357326.
  • Н.А. Вавилов. Не совсем наивная теория множеств. — Санкт-Петербург: СПбГУ, 2008.

Ссылки[править | править код]

Источник — https://ru.wikipedia.org/w/index.php?title=Непересекающиеся_множества&oldid=137428546