Геодезические на эллипсоиде

Геодезическая на плоском эллипсоиде

Изучение геодезических на эллипсоиде возникло в связи с задачами геодезии, а именно с обработкой сетей триангуляции. Фигура Земли хорошо описывается эллипсоидом вращения, слегка сплющенной сферой. Геодезическая (геодезическая линия) это кратчайший путь между двумя точками на кривой поверхности, на плоскости он обращается в прямую. Таким образом, обработка сети триангуляции на эллипсоиде использует ряд задач сфероидической тригонометрии(Эйлер 1755).

Если рассматривать Землю как сферу, то геодезические являются большими кругами (все из которых замкнуты) и задача сводится к сферической тригонометрии. Однако, Ньютон (1687) показал, что эффект вращения Земли приводит к сжатию, соответственно фигура общается в сплюснутый эллипсоид вращения, в этом случае только экватор и меридианы являются простыми замкнутыми геодезическими. Кроме того, кратчайший путь между двумя точками на экваторе необязательно проходит вдоль экватора. Наконец, если эллипсоид преобразовать в трехосный (с тремя различными полуосями), то только три геодезических линий будут замкнутыми.

Геодезические на эллипсоиде вращения

Есть несколько способов определения геодезических (Гильберт & Кон-Фоссен 1952, С. 220–221). Простое определение — кратчайший путь между двумя точками на поверхности. Однако, в общем случае более полезно определять гедезические как пути с нулевой геодезической кривизной, аналог прямых на искривленной поверхности. Это определение охватывает геодезические, протяженные так далеко по поверхности эллипсоида (несколько больше половины полуокружности) что другие различные маршруты требуют меньшего расстояния. Локально эти геодезические все еще идентичны кратчайшему расстоянию между двумя точками.

К концу 18 века эллипсоид вращения (аналогичен термину сфероид) являлся принятым и используемым приближением фигуры Земли. Обработка сетей триангуляции влечет за собой редукцию всех измерений к референц-эллипсоиду и решению исходной задачи на плоскости как задачи сфероидической тригонометрии (Бомфорд 1952, Гл. 3) (Лейк и др. 2015, §4.5).

Рис. 1. Геодезическая AB на эллипсоиде вращения. N — северный полюс. EFH лежит на экваторе.

Возможно свести все различные геодезические задачи к двум типам. Рассмотрим две точки: точка A с широтой φ₁ и долготой λ₁ и B с широтой φ₂ и долготой λ₂ (см Рис. 1). Соединяющая их геодезическая (от A к B) это AB, с длиной s₁₂, у которой есть азимуты α₁ и α₂ в двух конечных точках. Под двумя геодезическими задачами обычно понимают следующее:

1. Прямая геодезическая задача или первая геодезическая задача, в которой, имея исходные A, α₁, и s₁₂, определяют B и α₂;
2. Обратная геодезическая задача или вторая геодезическая задача, в которой даны A и B, и требуется найти s₁₂, α₁, и α₂.

Как видно из Рис. 1, решение этих проблем включает в себя решение треугольника NAB где дан один угол, α₁ для прямой задачи и λ₁₂ = λ₂ − λ₁ для обратной задачи, а также две его смежные стороны. Для сферы решение этих главных задач сводится к простым задачам сферической тригонометрии, решение которых сводится к формулам для решения сферического треугольника. (См. статью Навигация по большому кругу.)

Для эллипсоида вращения, характерная константа, определяющая геодезическую была найдена Клеро (1735). А систематическое решение для путей геодезических было дано Лежандром (1806) и Ориани (1806) (а также последующими работами в 1808 и 1810). Полное решение прямой задачи (в комплексе с вычислительными таблицами и примером вычислений) дал Бессель (1825).

На протяжении 18 века геодезические, как правило, называли "кратчайшими линиями". Термин "геодезическая линия" был введен Лапласом (1799):

Nous désignerons cette ligne sous le nom de ligne géodésique [Мы будем называть эту линию геодезическая линия].

Этот термин вошел в английский язык как "геодезическая линия" или "геодезическая", как пример (Хаттон 1811),

A line traced in the manner we have now been describing, or deduced from trigonometrical measures, by the means we have indicated, is called a geodetic or geodesic line: it has the property of being the shortest which can be drawn between its two extremities on the surface of the Earth; and it is therefore the proper itinerary measure of the distance between those two points. [Линия, пролегающая в форме, которую мы описали, или выведенная из тригонометрических измерений, как мы указали, называется геодезической или геодезической линией: она имеет свойство быть самой короткой, которую можно провести между двумя пунктами на поверхности Земли; и, следовательно, истинным путем измерения расстояния между двумя этими пунктами.]

В применении к другим областям, термин геодезическая линия, часто сокращается до геодезической, которой было отдано предпочтение.

Этот раздел рассматривает задачу на эллипсоиде вращения (как сплюснутого, так и вытянутого). Задача на трехосном эллипсоиде рассматривается в следующем разделе.

Уравнения для геодезической

Рис.2.Дифференциальный элемент меридионального эллипса.

Рис.3.Дифференциальный элемент геодезической на эллипсоиде.

Здесь выведены уравнения для геодезической; Данный вывод объединяет уравнения Бесселя (1825). Йордана & Эггерта (1941), Багратуни (1962, §15), Ганшина (1967, Chap. 5), Краковски & Томпсона (1974, §4), Раппа (1993, §1.2), Джекелея (2012), and Бора & Странга (2012).

Рассмотрим эллипсоид вращения с экваториальным радиусом a и полярным радиусом b. Определим сжатие f = (a − b)/a, эксцетриситет e = ${\sqrt {a^{2}-b^{2}}}/a$, и второй эксцентриситет e′ = ${\sqrt {a^{2}-b^{2}}}/a$ = e/(1 − f). (В большинстве случаев, в геодезии применяется сплюснутый эллипсоид a > b; однако, в теории применяется вытянутый эллипсоид, a < b, причем в этом случае f, e², и e′² отрицательные.)

Пусть элементарный отрезок пути на эллипсоиде имеет длину ds. Из Рис. 2 и 3, мы видим что если известен его азимут α, то ds связан с dφ и dλ следующим образом

(1)${\color {white}.}\qquad \cos \alpha \,ds=\rho \,d\varphi =-{\frac {dR}{\sin \varphi }},\quad \sin \alpha \,ds=R\,d\lambda ,$

где ρ представляет собой радиус кривизны меридиана, R = ν cosφ радиус круга с широтой φ, и ν представляет собой радиус нормального сечения. Следовательно элементарный отрезок равен

$ds^{2}=\rho ^{2}\,d\varphi ^{2}+R^{2}\,d\lambda ^{2}$

или

${\begin{aligned}ds&={\sqrt {\rho ^{2}\varphi '^{2}+R^{2}}}\,d\lambda \\&\equiv L(\varphi ,\varphi ')\,d\lambda ,\end{aligned}}$

Где φ′ = dφ/dλ и

функция Лагранжа L отражающая зависимость φ от ρ(φ) и R(φ). Длина произвольной линии между (φ₁, λ₁) and (φ₂, λ₂) задается

$s_{12}=\int _{\lambda _{1}}^{\lambda _{2}}L(\varphi ,\varphi ')\,d\lambda ,$

где φ функция от λ удовлетворяющих φ(λ₁) = φ₁ и φ(λ₂) = φ₂. Кратчайший путь или геодезическая находится через функцию φ(λ). Это задача в области вариационного исчисления и связана с минимизацией условий. Оно задается с помощью тождества Бальтрами,

$L-\varphi '{\frac {\partial L}{\partial \varphi '}}={\text{const.}}$

Подставляя L и применяя Форм. (1) получим

$R\sin \alpha ={\text{const.}}$

Клеро (1735) вывел это соотношение, используя геометрическую конструкцию; аналогичный вывод получен Люстерником (1964, §10). Дифференцируя это соотношение получим

$d\alpha =\sin \varphi \,d\lambda .$

Данное равенство совместно с уравнением (1) приводит к системе обыкновенных дифференциальных уравнений для геодезической

${\color {white}.}\qquad {\frac {d\varphi }{ds}}={\frac {\cos \alpha }{\rho }};\quad {\frac {d\lambda }{ds}}={\frac {\sin \alpha }{\nu \cos \varphi }};\quad {\frac {d\alpha }{ds}}={\frac {\tan \varphi \sin \alpha }{\nu }}.$

Мы можем выразить R через приведенную широту β

$R=a\cos \beta ,$

и соотношение Клеро примет вид

$\sin \alpha _{1}\cos \beta _{1}=\sin \alpha _{2}\cos \beta _{2}.$

Рис.4.Геодезическая задача, отображенная на вспомогательной сфере.

Рис.5.Элементарная геодезическая задача на вспомогательной сфере.

Это синусоидальное правило сферической тригонометрии устанавливающее связь между двумя сторонам треугольника NAB (см. Рис. 4) NA = 1⁄2π − β₁ и NB = 1⁄2π − β₂ и противолежащими углам B = π − α₂ и A = α₁.

Для того чтобы найти соотношение для третьей стороны AB = σ₁₂, сферической длины дуги, и прилежащего угла N = ω₁₂, сферической долготы, полезно рассмотреть треугольник NEP, представляющий собой геодезическую, берущую начало на экваторе (см. рис. 5). На этом рисунке элементы, отнесенные к вспомогательной области, приведены с указанными в скобках значениями на эллипсоиде. Величины без индексов относятся к произвольной точке P. E - точка , в которой геодезическая пересекает экватор, используется в качестве начала отчета для σ, s и ω.

Рис. 6. Дифференциальные элементы геодезической на сфере.

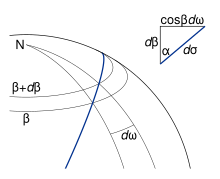
Если сторону EP увеличить путем перемещения P в бесконечность (см. Рис. 6), получим

(2)${\color {white}.}\qquad \cos \alpha \,d\sigma =d\beta ,\quad \sin \alpha \,d\sigma =\cos \beta \,d\omega .$

Комбинация формул (1) и (2) дает дифференциальное уравнение для s и λ

${\frac {1}{a}}{\frac {ds}{d\sigma }}={\frac {d\lambda }{d\omega }}={\frac {\sin \beta }{\sin \varphi }}.$

Соотношение β и φ

$\tan \beta ={\sqrt {1-e^{2}}}\tan \varphi =(1-f)\tan \varphi ,$

дает

${\frac {\sin \beta }{\sin \varphi }}={\sqrt {1-e^{2}\cos ^{2}\beta }},$

таким образом дифференциальное уравнение для геодезической примет вид

${\frac {1}{a}}{\frac {ds}{d\sigma }}={\frac {d\lambda }{d\omega }}={\sqrt {1-e^{2}\cos ^{2}\beta }}.$

Последний шаг состоит в использовании σ в качестве независимого параметра в обоих дифференциальных уравнениях для выражения s и λ в интегральном виде. Применение синусоидальное правила к вершинам E и G в сферическом треугольнике EGP на Рис. 5 дает

$\sin \beta =\sin \beta (\sigma ;\alpha _{0})=\cos \alpha _{0}\sin \sigma ,$

где α₀ азимут при вершине E. Подставляя в уравнение для ds/dσ и интегрируя получим

(3)${\color {white}.}\qquad {\frac {s}{b}}=\int _{0}^{\sigma }{\sqrt {1+k^{2}\sin ^{2}\sigma '}}\,d\sigma ',$

где

$k=e'\cos \alpha _{0},$

причем вводится ограничение s(σ = 0) = 0. Лежандр (1811, p. 180) указывает на то, что уравнение для s такое же, как уравнение для дуги на эллипсоиде с полуосями b= ${\sqrt {1+e'cos^{2}\alpha _{0}}}$ и b. Для того, чтобы выразить уравнение для λ через σ, запишем

$d\omega ={\frac {\sin \alpha _{0}}{\cos ^{2}\beta }}\,d\sigma ,$

что следует из уравнения (2) и соотношения Клеро. Это позволяет получить

(4)${\color {white}.}\qquad \lambda -\lambda _{0}=\omega -f\sin \alpha _{0}\int _{0}^{\sigma }{\frac {2-f}{1+(1-f){\sqrt {1+k^{2}\sin ^{2}\sigma '}}}}\,d\sigma ',$

причем применяются следующие ограничения: λ = λ₀ на пересечении экватора и σ = 0.

Это завершает нахождение длины геодезической с использованием вспомогательной сферы. Использование данного способа позволяет точно сопоставить большой круг с геодезической на эллипсоиде вращения.

Существует также несколько способов аппроксимации геодезических на земном эллипсоиде ( с малым сжатием) (Рапп 1991, §6); некоторые из них описаны в статье о географическом расстоянии. Тем не менее, они, как правило, сопоставимы по сложности точному решению Джекелея (Джекелей 2012, §2.1.4).

Поведение геодезических

Рис. 7. Только меридиан и экватор являются замкнутыми геодезическими. (Для крайне сжатого эллипсоида существуют другие замкнутые геодезические; см Рис. 11 и 12).

Рис.8.Геодезическая на плоском эллипсоиде (f = 1⁄50) с α₀ = 45 °.Движение геодезической линии на эллипсоиде примерно по 5 контурам.

Рис.9.Движение той же геодезической по 70 контурам.

Рис. 10. Геодезические на вытянутом эллипсоиде (f = −1⁄50) c α₀ = 45 °. Сравним с Рис. 8.

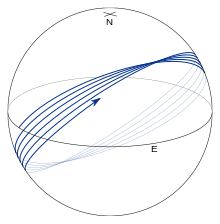
На Рис. 7 показаны простые замкнутые геодезические, которые состоят из меридианов (зеленые) и экватора (красный). (Здесь под определением "простая" подразумевается, что геодезическая замыкается без промежуточного самопересечения.) Это следует из уравнений для геодезических, приведенных в предыдущем разделе.

Все остальные геодезические олицетворяются Рис. 8 и 9 которые показывают геодезические начиная от экватора с α₀ = 45°. Геодезическая колеблется вокруг экватора. Пересечения экватора называются узлы, а точки максимума и минимума широты называются вершинами; вершины широты задаются: β = ±(1⁄2π − |α₀|). Геодезическая совершает одно полное колебание в широте до того, как долгота увеличится на 360 deg. Таким образом, на каждом последующем северном пересечении экватора (см Рис. 8), λ отстает от полного круга экватора приблизительно на 2π f sinα₀ (для вытянутого эллипсоида эта величина отрицательна и λ совершает более, чем один полный круг; см Рис. 10). Почти для всех значений α₀, геодезическая покроет область эллипсоида между двумя параллелями с максимальной и минимальной широтой (см Рис. 9).

Рис.11.Две дополнительные замкнутые геодезические для плоского эллипсоида, b⁄a = 2⁄7 (вид с боку)

Рис.12.Две дополнительные замкнутые геодезические для плоского эллипсоида, b⁄a = 2⁄7 (вид сверху)

Если эллипсоид достаточно сплюснутый, т.е., b⁄a < 1⁄2, возможен еще один вид простых замкнутых геодезических (Клингенберг 1982, §3.5.19). Две такие геодезические показаны на Рис. 11 и 12. Здесь b⁄a = 2⁄7 и экваториальный азимут, α₀, для зеленой (соотв. синей) геодезической задан как 53,175 deg (соотв. 75,192 deg), так что геодезическая совершает 2 (соотв. 3) полных колебания относительно экватора на одном круге по эллипсоиду.

Рис. 13. Геодезические (синим) от одной точки при f = 1⁄10, φ₁ = −30 °; геодезические круги показаны зеленым, множество раздела катлокус показано красным.

На Рис. 13 показаны геодезические (синим) исходящие из A с α₁, кратным 15 deg вплоть до то точки, в которой они перестают быть кратчайшими путями. (Сжатие было увеличено до 1⁄10 чтобы подчеркнуть эллипсоидальные эффекты.) Также показаны (зеленым) кривые с построянной s₁₂, которые являются геодезическими окружностями с центром A. Гаусс (1828) показал, что на любой поверхности, геодезические и геодезический круг пересекаются под прямым углом. Красная линия — множество раздела(катлокус), множество точек, которые имеют несколько (в данном случае две) кратчайших геодезических из A. На сфере, катлокус является точкой. На сплющенном эллипсоиде (показанном здесь) он представляет собой сегмент параллели с центром в точке, диаметрально противоположной A, φ = −φ₁. Протяженность катлокуса по долготе приблизительно λ₁₂ ∈ [π − f π cosφ₁, π + f π cosφ₁]. Если A лежит на экваторе, φ₁ = 0, это соотношение является точным и, как следствие, экватор является кратчайшей геодезической, только если выполняется условие |λ₁₂| ≤ (1 − f)π. Для вытянутого эллипсоида, катлокус представляет собой сегмент анти-меридиана с центром в точке, диаметрально противоположной A, λ₁₂ = π, и это означает, что меридианные геодезические перестают быть кратчайшими путями при достижении противоположной точки.

Решение прямых и обратных задач

Решение геодезических задач подразумевает проектирование геодезических на вспомогательную сферу и решение соответствующих задач по большому кругу. При решении "элементарного" сферического треугольника NEP на Рис. 5,

по правилу Непера получим,

${\begin{aligned}\sin \alpha _{0}&=\sin \alpha \cos \beta =\tan \omega \cot \sigma ,\\\cos \sigma &=\cos \beta \cos \omega =\tan \alpha _{0}\cot \alpha ,\\\cos \alpha &=\cos \omega \cos \alpha _{0}=\cot \sigma \tan \beta ,\\\sin \beta &=\cos \alpha _{0}\sin \sigma =\cot \alpha \tan \omega ,\\\sin \omega &=\sin \sigma \sin \alpha =\tan \beta \tan \alpha _{0}.\end{aligned}}$

Определение геодезических включает в себя решение интегралов для расстояния, s, и долготы, λ, Ур. (3) и (4) которые, в свою очередь, зависят от параметра α₀.

Решение прямой задачи не вызывает сложности, потому что α₀ может быть определен непосредственно из заданных величин φ₁ и α₁.

В случае обратной задачи, λ₁₂ задана; из этого нельзя быстро перейти к эквивалентному сферическому углу ω₁₂, потому что α₀ неизвестен. Таким образом, для решения задачи требуется находить α₀ итеративно.

В геодезии, где f мал, интегралы раскладываются в ряд (Лежандр 1806) (Ориани 1806) (Бессель 1825) (Гельмерт 1880) (Рэйнсфорд 1955) (Рапп 1993). Для любых f, интегралы (3) и (4) могут быть найдены численно или выражением их в эллиптические интегралы (Лежандр 1806) (Кэли 1870).

Винсенти (1975) предоставляет решения для прямых и обратных задач; они основаны на разложении в ряд до третьего порядка в сжатии и обеспечивают точность около 0,1 mm для эллипсоида WGS84; однако обратный метод не сходится для практически диаметрально противоположных точек. Карни (2013) продолжает разложение до шестого порядка, чего достаточно для обеспечения полной двойной точности для |f| ≤ 1⁄50 и повышает точность решения обратной задачи, так, что она сходится во всех случаях. Карни (2013, addendum) расширил возможности использования эллиптических интегралов, которые могут быть применены к эллипсоидам с произвольным сжатием.

Различные свойства геодезических

Различные задачи, связанные с геодезическими требуют знания об их поведении при возмущении. Это полезно при уравнивании тригонометрии (Элерт 1993), определение физических свойств сигналов, проходящих по геодезической, и т.д. Рассмотрим опорную геодезическую, выраженную как s, и другую геодезическую на малом расстоянии t(s) от первой. Гаусс (1828) показал, что t(s) удовлетворяют уравнению Гаусса-Якоби

${\color {white}.}\qquad \displaystyle {\frac {d^{2}t(s)}{ds^{2}}}=K(s)t(s),$

Рис. 14. Определение приведенной длины и масштаба геодезической.

где K(s) является Гауссовой кривизной для s. В качестве второго порядка линейного однородного дифференциального уравнения, его решение может быть выражено как сумма двух независимых решений

$t(s_{2})=Cm(s_{1},s_{2})+DM(s_{1},s_{2})$

где

${\begin{aligned}m(s_{1},s_{1})&=0,\quad \left.{\frac {dm(s_{1},s_{2})}{ds_{2}}}\right|_{s_{2}=s_{1}}=1,\\M(s_{1},s_{1})&=1,\quad \left.{\frac {dM(s_{1},s_{2})}{ds_{2}}}\right|_{s_{2}=s_{1}}=0.\end{aligned}}$

Величина m(s₁, s₂) = m₁₂ является так называемой уменьшенной длиной, и M(s₁, s₂) = M₁₂ масштабом геодезической. Их основные определения приведены на Рис. 14.

Гауссова кривизна для эллипсоида вращения:

$K={\frac {1}{\rho \nu }}={\frac {{\bigl (}1-e^{2}\sin ^{2}\varphi {\bigr )}^{2}}{b^{2}}}={\frac {b^{2}}{a^{4}{\bigl (}1-e^{2}\cos ^{2}\beta {\bigr )}^{2}}}.$

Гельмерт (1880, Eq. (6.5.1.)) решил уравнение Гаусса-Якоби для этого случая, позволяющим выразить m₁₂ and M₁₂ в интегральной форме.

Как видно из Рис. 14 (верхний подрисунок), разделение двух геодезических, начиная с одно и той же точки с азимутами, различающимися на dα₁ представляется как m₁₂ dα₁. На замкнутый поверхности, например на эллипсоиде, m₁₂ колеблется около нуля. Точка, в которой m₁₂ обращается в ноль, это точка сопряженная с исходной точкой. Для геодезической между A и B, длиной s₁₂, чтобы быть кратчайшим путем, необходимо удовлетворять условию Якоби (Якоби 1837) (Якоби 1866, §6) (Форсайт 1927, §§26–27) (Блисс 1916), так что нет никакого смысла сопрягать A между A и B. Если это условие не выполняется, то поблизости есть путь (не обязательно являющийся геодезической), который короче. Таким образом, условие Якоби является локальным свойством геодезической и необходимым условием, при котором геодезическая является кратчайшим путем. Необходимые и достаточные условия для того, чтобы геодезическая являлась кратчайшим путем:

• для сжатого эллипсоида, |σ₁₂| ≤ π;
• для вытянутого эллипсоида, |λ₁₂| ≤ π, если α₀ ≠ 0; если α₀ = 0, то дополнительное условие m₁₂ ≥ 0 требуется, если |λ₁₂| = π.

Конверт геодезической

Рис. 15. Конверт геодезической в точке A с φ₁ = −30 ° (f = 1⁄10, φ₁ = −30 °)

Рис. 16. Четыре геодезические линии, соединяющие точку A с точкой B, φ₂ = 26 °, λ₁₂ = 175 ° (f = 1⁄10, φ₁ = −30 °)

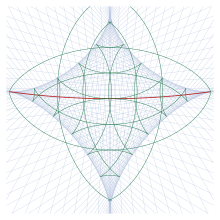
Геодезические, проведенные из определенной точки A, если они продолжаются после точки разрыва, образуют конверт изображенный на Рис. 15. Здесь геодезические для которых α₁ кратен 3 ° Показаны голубым цветом. (Геодезические показаны только для первого прохождения вблизи точки-антипода) Геодезические окружности показаны зеленым цветом; Они образуют на конверте зажимы. Место разреза показано красным цветом. Конверт - это место сопряженных с A точек; точки на конверте могут быть вычислены путем нахождения точки, в которой m₁₂ = 0 на геодезической. Якоби (1891) называет эту звезду рисунком полученным в конверте Астроиды.

За пределами астроиды две геодезические пересекаются в каждой точке. Таким образом там имеются две геодезические линии между точкой А и этими точками. Это соответствует ситуации на той сфере, где есть "короткие" и "длинные" линии по большой окружности между двумя точками. Внутри же астроиды четыре геодезические пересекаются в каждой точке. Четыре таких геодезических показаны на Рис. 16, где геодезические пронумерованы в порядке увеличения длины. (На этом рисунке используется такое же как на Рис.13 положение точки A и изображается в той же проекции.) Две кротчайшие геодезические являются стабильными, т.е., m₁₂ > 0, причем нет другой более короткой линии, соединяющей две точки; другие две нестабильны. Только самая короткая (первая) линия имеет σ₁₂ ≤ π. Все геодезические являются касательными к конверту, который показан зеленым цветом на рисунке.

Астроида (внешне) эволюта геодезических кругов с центром в точке A. Аналогично, геодезические являются эвольвентой астроиды.

Площадь геодезического полигона

Геодезический полигон - это полигон, сторонами которого являются геодезические. Такой полигон можно найти, предварительно вычислив площадь между отрезком геодезической и экваторм, т. е. площадь четырехугольника AFHB на Рис. 1 (Даниельсен 1989). Когда это площадь известна, площадь полигона может быть вычислена путем суммирования областей всех ребер полигона.

Выражение для области S₁₂ в AFHB разработано Сьобергом (2006). Площадью любой закрытой области эллипсоида можно найти по формуле

$T=\int dT=\int {\frac {1}{K}}\cos \varphi \,d\varphi \,d\lambda ,$

где dT элемент площади поверхности, а K - Гауссова кривизна. Приведем теорему Гаусса-Бонне, применяемую для геодезических полигонов

$\Gamma =\int K\,dT=\int \cos \varphi \,d\varphi \,d\lambda ,$

где

$\Gamma =2\pi -\sum _{j}\theta _{j}$

является геодезическим избытком и θ_j внешний угол при вершина j. Увеличив уравнение на величину ΓR₂², где R₂ - подлинный радиус, вычитание которого из уравнения для T дает

${\begin{aligned}T&=R_{2}^{2}\,\Gamma +\int {\biggl (}{\frac {1}{K}}-R_{2}^{2}{\biggr )}\cos \varphi \,d\varphi \,d\lambda \\&=R_{2}^{2}\,\Gamma +\int {\Biggl (}{\frac {b^{2}}{{\bigl (}1-e^{2}\sin ^{2}\varphi {\bigr )}^{2}}}-R_{2}^{2}{\Biggr )}\cos \varphi \,d\varphi \,d\lambda ,\end{aligned}}$

где K было заменено значением кривизны для эллипсоида. Применяя эту формулу к четырехугольнику AFHB и заметив, что Γ = α₂ − α₁ проинтегрируем по φ

$S_{12}=R_{2}^{2}(\alpha _{2}-\alpha _{1})+b^{2}\int _{\lambda _{1}}^{\lambda _{2}}{\biggl (}{\frac {1}{2{\bigl (}1-e^{2}\sin ^{2}\varphi {\bigr )}}}+{\frac {\tanh ^{-1}(e\sin \varphi )}{2e\sin \varphi }}-{\frac {R_{2}^{2}}{b^{2}}}{\biggr )}\sin \varphi \,d\lambda ,$

де Интеграл находится над геодезической линией (так, что φ является косвенной функцией от λ). Интеграл может быть выражен в виде ряда, допустимого для малых f (Даниельсен 1989) (Карней 2013, §6 и добавление).

Площадь геодезического полигона задается суммированием S₁₂ по его сторонам. Этот результат выполняется при условии, что полигон не включает полюс; если же включает, то к сумме должно быть добавлено 2π R₂². Если ребра заданы их вершинами, то удобным выражением для геодезического избытка E₁₂ = α₂ − α₁ является

$\tan {\frac {E_{12}}{2}}={\frac {\sin {\tfrac {1}{2}}(\beta _{2}+\beta _{1})}{\cos {\tfrac {1}{2}}(\beta _{2}-\beta _{1})}}\tan {\frac {\omega _{12}}{2}}.$

Геодезические на трехосном эллипсоиде

Трехосная система координат

Рассмотрим эллипсоид, определяемый по формуле

$h={\frac {X^{2}}{a^{2}}}+{\frac {Y^{2}}{b^{2}}}+{\frac {Z^{2}}{c^{2}}}=1,$

где (X,Y,Z) декартовы координаты с началом в центре эллипсоида и без потери примем обобщение, a ≥ b ≥ c > 0. Якоби (1866, §§26–27) установил что эллипсоидальные широты и долготы (β, ω) определяются следующим образом:

Рис. 17. Эллипсоидальные координаты.

${\begin{aligned}X&=a\cos \omega {\frac {\sqrt {a^{2}-b^{2}\sin ^{2}\beta -c^{2}\cos ^{2}\beta }}{\sqrt {a^{2}-c^{2}}}},\\Y&=b\cos \beta \sin \omega ,\\Z&=c\sin \beta {\frac {\sqrt {a^{2}\sin ^{2}\omega +b^{2}\cos ^{2}\omega -c^{2}}}{\sqrt {a^{2}-c^{2}}}}.\end{aligned}}$

в пределе b → a, β становится параметрической широтой для сплющенного эллипсоида, поэтому использование символа β согласуется с предыдущими разделами.. Однако, ω отлична от сферической долготы, определяемой выше.

Линии сетки константы β (показаны синим цветом) и ω (показаны зеленым цветом) изображены на Рис. 17. Это константа позволяет создать ортогональную систему координат: линии сетки пересекаются под прямым углом. Основными сечениями эллипсоида являются показанные красным цветом X = 0 и Z = 0. Третий основной разрез, Y = 0, образуется линиями β = ±90° и ω = 0° or ±180°. Эти линии пересекаются в четырех точках округления (две из которых видны на этом рисунке), где главные радиусы кривизны равны между собой. Здесь и на других рисунках в секциях в качестве параметров эллипсоида принято a:b:c = 1.01:1:0.8 и рассматривается ортогональная проекция для точки с φ = 40°, λ = 30°.

Линии сетки эллипсоидальных координат могут быть определены в трех направлениях разными способами :

1. Они являются "линиями кривизны" на эллипсоиде: они параллельны направлениям главной кривизны (Мунге 1796).
2. Они также являются пересечениями эллипсоида с конфокальной системой гиперболоидов из одного и двух листов (Дюпен 1813, Часть 5).
3. Наконец , они являются геодезическими эллипсами и гиперболами, определенными с использованием двух соседних точек округления (Гильберт & Кон-Фоссен 1952, С. 188). Например, линии с постоянной β на Рис. 17 может быть сгенерирована с помощью привычной струнной конструкции для эллипсов с концами струны, прикрепленными к двум точкам округления.

Решение Якоби

Якоби показал, что геодезические уравнения, выраженные через эллипсоидальные координаты, являются разделяемыми. Вот как он рассказывал о своем открытии другу и соседу Бесселю (Якоби 1839, Письмо к Бесселю),

Позавчера я свел к квадратуре задачу геодезической линии на эллипсоиде с тремя неравными осями. Это самые простые формулы в мире, Абелевы интегралы, которые становятся хорошо известными эллиптическими интегралами, если две оси заданы равными.

Кёнигсберг, 28 декабря '38.

Решение Якоби имеет вид (Якоби 1839) (Якоби 1866, §28)

${\begin{aligned}\delta &=\int {\frac {{\sqrt {b^{2}\sin ^{2}\beta +c^{2}\cos ^{2}\beta }}\,d\beta }{{\sqrt {a^{2}-b^{2}\sin ^{2}\beta -c^{2}\cos ^{2}\beta }}{\sqrt {{\bigl (}b^{2}-c^{2}{\bigr )}\cos ^{2}\beta -\gamma }}}}\\[6pt]&\quad -\int {\frac {{\sqrt {a^{2}\sin ^{2}\omega +b^{2}\cos ^{2}\omega }}\,d\omega }{{\sqrt {a^{2}\sin ^{2}\omega +b^{2}\cos ^{2}\omega -c^{2}}}{\sqrt {{\bigl (}a^{2}-b^{2}{\bigr )}\sin ^{2}\omega +\gamma }}}}.\end{aligned}}$

Как отмечает Якоби "функция угла β равна функции угла ω. Эти две функции представляют собой только Абелевы интегралы..." В решении появляются две константы δ и γ . Обычно δ равно нулю если нижние пределы интегралов в начальной точке геодезической равны и направление геодезической определяется по формуле γ. Однако, для геодезической начинающейся в точке округления мы имеем γ = 0 и δ, определяющую направление в точку округления. Константа γ может быть найдена следующим образом

$\gamma ={\bigl (}b^{2}-c^{2}{\bigr )}\cos ^{2}\beta \sin ^{2}\alpha -{\bigl (}a^{2}-b^{2}{\bigl )}\sin ^{2}\omega \cos ^{2}\alpha ,$

где α между геодезической и линией с постоянным значением ω. В пределе b → a, что позволяет получить равенство sinα cosβ = const., являющееся знакомым соотношением Клеро. Вывод решения Якоби приведен у Дарби (1894, §§583–584); он приводит решение найденное Луивиллем (1846) для общей квадратичной поверхности.

Изучение трехосных геодезических

Рис.18.Циркумполярные геодезические с ω₁ = 0 °, α₁ = 90 °, β₁ = 45,1 °..

Рис.19.Циркумполярные геодезические с ω₁ = 0 °, α₁ = 90 °, β₁ = 87,48 °..

На триаксиальном эллипсоиде существует только три простых замкнутых геодезических: три главных сечения эллипсоида, для которого X = 0, Y = 0 и Z = 0 . Для изуения других геодезических, удобно рассматривать геодезические которые пересекают среднее основное сечение, Y = 0, под прямым углом. Такие геодезические линии показаны на Рис. 18–22, которые используют те же параметры эллипсоида и рассматриваются под таким же углом, что и на Рис. 17. Кроме того, показаны три главных эллипса красным цветом на каждом из этих рисунков.

Если начальная точка имеет координаты β₁ ∈ (−90°, 90°), ω₁ = 0, и α₁ = 90°, то γ > 0 и геодезическая окружает эллипсоид в "циркумполярном" смысле. Геодезическая линия смещается к северу и югу от экватора; при каждом смещении он совершает чуть меньше, чем полный круг вокруг эллипсоида в результате, как правило, геодезическая заполняет всю область ограниченную параллелями с широтами β = ±β₁. Два примера приведены на Рис. 18 и 19. Рисунок 18 показывает практически такое же поведение, что и для сплющенного эллипсоида вращения(так как a ≈ b); сравните с Рис. 9. Однако, если начальная точка находится на более высокой широте (Рис. 18), искажения, возникающие в результате a ≠ b очевидны. Все касательные к циркумполярной геодезической линии соприкасаются с конфокальной однолистовым гиперболоидом, пересекающим эллипсоид при β = β₁ (Шаль 1846) (Гильберт & Кон-Фоссен 1952, С. 223–224).

Рис.20.Трансполярные геодезические β₁ = 90 °, α₁ = 180 °, ω₁ = 39,9 °.

Рис.21.Трансполярные геодезические β₁ = 90 °, α₁ = 180 °, ω₁ = 9,966 °.

Если начальная точка имеет координаты β₁ = 90°, ω₁ ∈ (0°, 180°), и α₁ = 180°, то γ < 0 и геодезическая окружает эллипсоид в" трансполярном " смысле. Геодезическая колеблется к востоку и западу от эллипса с X = 0; на каждом колебании она совершает чуть больше, чем полный круг вокруг эллипсоида. Как правило, это приводит к заполнению геодезической всей области ограниченной параллелями с долготами ω = ω₁ и ω = 180° − ω₁. Если a = b, то все меридианы являются геодезическими; эффект от a ≠ b вызывает такие геодезические колебания на восток и Запад. Два примера приведены на Рис. 20 и 21. Сужение геодезическая вблизи полюса исчезает в пределе b → c; в этом случае эллипсоид становится вытянутым, и Рис. 20 будет напоминать Рис. 10 (поворачивается на бок). Все касательные к трансполярной геодезической касаются конфокального двухслойного гиперболоида пересекающий эллипсоид при ω = ω₁.

Рис. 22. Круговая геодезическая, β₁ = 90 °, ω₁ = 0 °, α₁ = 135 °.

Если начальная точка имеет координаты β₁ = 90°, ω₁ = 0° (точка округления), и α₁ = 135° (геодезический пересекает эллипс Y = 0 под прямым углом), то γ = 0 и геодезическая неоднократно пересекает противоположную точку округления и возвращается к своей начальной точке. Однако на каждом circuit угол, под которым он пересекает Y = 0 становится ближе к 0 ° или 180 ° так что асимптотически геодезическая лежит на эллипсе Y = 0 (Харт 1849) (Арнольд 1989, С. 265), как показано на Рис. 22. Одна геодезическая не заполняет область на эллипсоиде. Все касательные к круговой геодезической касаются конфокальной гиперболы, которая пересекает эллипсоид в точке округления.

Круговая геодезическая обладает несколькими интересными свойствами.

• Через любую точку на эллипсоиде проходят две круговые геодезические линии.
• Геодезическое расстояние между противоположными точками округления независимо от начального направления геодезической.
• В то время как замкнутые геодезические на эллипсах X = 0 и Z = 0 являются стабильными (геодезическая, изначально близкая к эллипсу и почти параллельная ему, остается близкой к эллипсу), замкнутая геодезическая на эллипсе Y = 0, которая проходит через все 4 точки округления, экспоненциально неустойчива. Если она будет возмущена,то будет колебаться в плоскости Y = 0 и перевернется, прежде чем вернуться к этой плоскости. (Это поведение может повторяться в зависимости от характера начального возмущения.)

Если начальная точка A геодезической не является круговой точкой, то ее оболочка - это астроид с двумя вершинами лежащими на β = −β₁ и двумя на ω = ω₁ + π. Локус разреза для точки A является частью линии β = −β₁ между вершинами.

Приложения

Прямая и обратная геодезические задачи ныне не занимают в геодезии центральную роль, которую занимали ранее. Вместо уравнивания геодезическая сеть как двухмернрой задачи сфероидической тригонометрии, эти проблемы сейчас решаются трехмерными методами(Винсенти & Бауринг 1978). Тем не менее, земные геодезической все еще играют важную роль в некоторых областях:

• в измерении расстояний и площадей в ГИС;
• в определении морских границ (UNCLOS 2006);
• для местной навигации, согласно правилам Федерального управления гражданской авиации (RNAV 2007);
• как метод измерения расстояний в ФАИ (FAI 2018).

По принцип наименьшего влияния, многие проблемы в физике могут быть сформулированы в виде дифференциальной задачи, аналогичной такой же для геодезических. Действительно, геодезическая эквивалентна отрезку пути движения частицы по поверхности, в отсутствии воздействия на нее каких-либо сил (Лаплас 1799a) (Гильберт & Кон-Фоссен 1952). По этой причине геодезические на простых поверхностях, таких как эллипсоид вращения или трехосный эллипсоид чаще используются в качестве "тестовых" при изучении новых методов. Примеры:

• исследование эллиптических интегралов (Лежандр 1811) и эллиптических функций (Вейерштрасс 1861);
• развитие дифференциальной геометрии (Гаусс 1828) (Кристоффель 1869);
• methods for solving systems of differential equations by a change of independent variables (Якоби 1839);
• изучение каустик (Якоби 1891);
• исследование числа и устойчивости периодических орбит (Пуанкаре 1905);
• в пределе c → 0, геодезические на трехосном эллипсоиде сводятся к динамическим бильярдам;
• расширения для произвольного числа измерений (Кноррер 1980);
• геодезический поток на поверхности (Бергер 2010, Chap. 12).

Смотрите также

• Географическая дальность
• Навигация по большому кругу
• Геодезическая
• Геодезия
• Дуга меридиана
• Румбовая линия
• Формулы Винсенти