Астроида
Перейти к навигации
Перейти к поиску

Астро́ида (от греч. αστρον — звезда и ειδος — вид, то есть звездообразная)[1] — плоская кривая, описываемая точкой окружности радиуса , катящейся по внутренней стороне окружности радиуса . Иначе говоря, астроида — это гипоциклоида с модулем .
История[править | править код]
Название кривой в форме «Astrois» предложил австрийский астроном Йозеф Иоганн фон Литров в 1838 г.[2][3][1]
Уравнения[править | править код]
Уравнение в декартовых прямоугольных координатах:
Параметрическое уравнение:[4]
Астроида также является алгебраической кривой 1 рода (и шестого порядка). Уравнение в алгебраическом виде:
Свойства[править | править код]

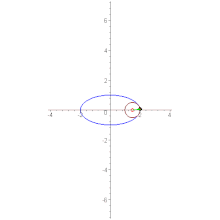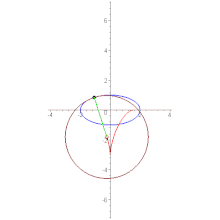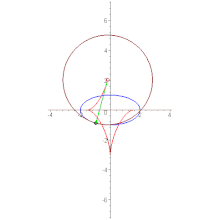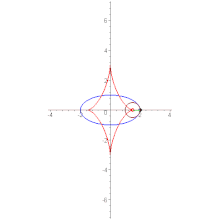
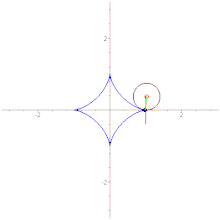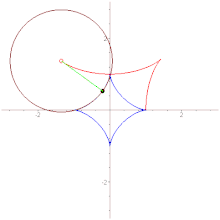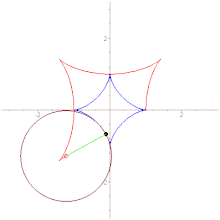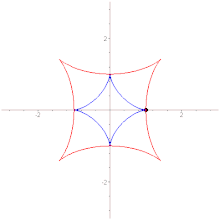
- Имеются четыре каспа.
- Длина дуги от точки с 0 до
- Длина всей кривой .
- Радиус кривизны:
- Площадь, ограниченная кривой:
- Объём тела вращения относительно любой координатной оси:
- Астроида является огибающей семейства отрезков постоянной длины, концы которых расположены на двух взаимно перпендикулярных прямых[1].
- Эволюта астроиды подобна ей, но вдвое больше неё и повёрнута относительно неё на 45°.
- Астроида (вытянутая вдоль оси) является эволютой эллипса[1]. В этом случае параметрическое выражение имеет вид:
- Неопределённый интеграл правой части последнего уравнения является интегралом от дифференциального бинома и равен
- Это выражение полезно при вычислении площадей элементов фигуры.
Примечания[править | править код]
- ↑ 1 2 3 4 Александрова, 2008, с. 17.
- ↑ J. J. v. Littrow. §99. Die Astrois // Kurze Anleitung zur gesammten Mathematik. — Wien, 1838. — P. 299.
- ↑ Loria, Gino. Spezielle algebraische und transscendente ebene kurven. Theorie und Geschichte. — Leipzig, 1902. — P. 224.
- ↑ Уравнение в прямоугольных координатах следует из параметрического уравнения и основного тригонометрического тождества. Вывод параметрического уравнения такой. Возьмём уравнение гипоциклоиды, подставим k=4. Синус/косинус тройного угла разложим по формуле синуса/косинуса суммы, то же для синуса/косинуса двойного угла. Учтём R=4r и получим наши уравнения.
- ↑ Lawrence J. D. A Catalog of Special Plane Curves, 1972, 1.1. Coordinate Systems, p. 4.
Литература[править | править код]
- Савёлов А. А. Плоские кривые: Систематика, свойства, применения. М.: Физматгиз, 1960. 293 с. Переиздана в 2002 году, ISBN 5-93972-125-7.
- Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник. — 3-е изд., испр. — М.: ЛКИ, 2008. — 248 с. — ISBN 978-5-382-00839-4.
- Lawrence J. D. A Catalog of Special Plane Curves. New York: Dover Publications, Inc., 1972. 218 p.














![{\displaystyle \int b{\bigg [}1-{\bigg (}{\frac {x}{a}}{\bigg )}^{\frac {2}{3}}{\bigg ]}^{\frac {3}{2}}dx={\frac {1}{16}}b\left({\sqrt {1-\left({\frac {x}{a}}\right)^{\frac {2}{3}}}}\left(-3a{\sqrt[{3}]{\frac {x}{a}}}+x\left(14-8\left({\frac {x}{a}}\right)^{\frac {2}{3}}\right)\right)+3a\arcsin \left({\sqrt[{3}]{\frac {x}{a}}}\right)\right)+C}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ae3a4b1c9373b0756313260473ab9282a142f73)