Форма Земли
Эту страницу предлагается объединить со страницей Сплюснутость Земли. |

Фо́рма Земли́ — термин для обозначения формы земной поверхности. В зависимости от определения фигуры Земли устанавливаются различные системы координат в геодезии.
История[править | править код]
Ещё в VI в. до нашей эры Пифагор считал, что Земля имеет шарообразную форму[1]. То же открытие наиболее авторитетный автор в этом вопросе, Феофраст, отдаёт Пармениду.
Через 200 лет Аристотель доказал это, ссылаясь на то, что во время лунных затмений тень Земли всегда круглая.
Спустя ещё 100 лет Эратосфен по разнице в отклонении солнечных лучей от вертикали в полдень летнего солцестояния определил, что окружность земного шара приблизительно в 50 раз больше расстояния от Сиены до Александрии. Однако неизвестно, насколько точно в то время было измерено расстояние между этими городами[2].
То, что форма Земли должна отличаться от шара, впервые показал Ньютон. Он предположил, что она имеет форму эллипсоида и предложил следующий мысленный эксперимент. Нужно прокопать две шахты: от полюса до центра Земли и от экватора до центра Земли. Эти шахты заливаются водой. Если Земля имеет форму шара, то глубина шахт одинакова. Но на воду в экваториальной шахте действует центробежная сила, в то время как на воду в полярной шахте — нет. Поэтому для равновесия воды в обеих шахтах необходимо, чтобы экваториальная шахта была длиннее[3].
Дальнейшее развитие теории фигуры Земли отражено в работах Гюйгенса, Кассини, Клеро, МакЛорена, д'Аламбера, Лагранжа, Лапласа, Лежандра, Якоби, Дирихле, Пуанкаре и др.
Современные представления[править | править код]
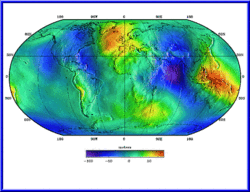
В нулевом приближении можно считать, что Земля имеет форму шара со средним радиусом 6371,3 км. Такое представление нашей планеты хорошо подходит для задач, точность вычислений в которых не превышает 0,5 %. В действительности Земля не является идеальным шаром. Из-за суточного вращения она сплюснута с полюсов; высоты материков различны; форму поверхности искажают и приливные деформации.
В геодезии и космонавтике для описания фигуры Земли обычно выбирают эллипсоид вращения или геоид. С геоидом связана система астрономических координат, с эллипсоидом вращения — система геодезических координат.
По определению, геоид — это поверхность, всюду нормальная силе тяжести[4].
Если бы Земля была целиком покрыта океаном и не подвергалась приливному воздействию других небесных тел и прочим подобным возмущениям, она имела бы форму геоида. В действительности в различных местах поверхность Земли может значительно отличаться от геоида. Для лучшей аппроксимации поверхности вводят понятие референц-эллипсоида, который хорошо совпадает с геоидом только на каком-то участке поверхности. Геометрические параметры референц-эллипсоидов отличаются от параметров среднего земного эллипсоида, который описывает земную поверхность в целом.
На практике используется несколько различных средних земных эллипсоидов и связанных с ними систем земных координат.
|
Здесь:
|
См. также[править | править код]
Примечания[править | править код]
- ↑ Диоген Лаэртский. КНИГА ВОСЬМАЯ. www.psylib.ukrweb.net. Дата обращения: 22 марта 2020. Архивировано 20 марта 2020 года.
- ↑ Трифонов Е.Д. Как измерили Солнечную систему // Природа. — Наука, 2008. — № 7. — С. 18—24. Архивировано 22 апреля 2013 года.
- ↑ Ещё раз о форме Земли — какая же она на самом деле? Архивная копия от 20 марта 2020 на Wayback Machine — Юный техник, № 11, 1975.
- ↑ В определение силы тяжести входит не только гравитационная, но и центробежная составляющая, поэтому геоид не совпадает с эквипотенциальной поверхностью чистого гравитационного поля; он, таким образом, всюду перпендикулярен не чистому вектору напряженности гравитационного поля, а отвесной линии.
Литература[править | править код]
- Жаров В. Е. Сферическая астрономия. — Москва, 2002.
Ссылки[править | править код]
- The shape of Planet Earth (англ.)
- Пантелеев В. Л. Теория фигуры Земли (курс лекций) на msu.ru
- Веб-сайт Международной Ассоциации Геодезии и Геофизики
- Белобров В. А. Была ли Земля плоской? на academia.edu

