Второе начало термодинамики
Второе начало термодинамики
[править | править код]Второ́е нача́ло термодина́мики (второй закон термодинамики) в современном изложении формулируется как объединённый принцип существования и возрастания некоторой функции состояния термодинамической системы ─ энтропии и вводит понятие абсолютной термодинамической температуры[1]. Таким образом, второе начало представляет собой закон об энтропии и её свойствах [2].
В изолированной системе энтропия либо остаётся неизменной, либо возрастает в неравновесных процессах, достигая максимума при установлении термодинамического равновесия (закон возрастания энтропии)[3][4]
Термин энтропия был образован Р. Клаузиусом из слова τροπη — превращение, и приставки ἐν — в, внутрь, в целом, обращение внутрь [5]. Понятие энтропии, точнее термодинамической или тепловой энтропии является ненаглядным, абстрактным и трудным для непосредственного восприятия, поскольку напрямую не вытекает из её математического выражения[6]. Понять и прочувствовать глубокий физический смысл энтропии легче по первоначальным формулировкам второго начала термодинамики, которые являются частными случаями более общей современной формулировки.
Второе начало термодинамики позволяет построить рациональную температурную шкалу, не зависящую от произвола в выборе термометрического свойства термодинамического тела и устройства для измерения температуры (термометра)[7]. Вместе первое и второе начала составляют основу феноменологической термодинамики, которую можно рассматривать как развитую систему следствий этих двух начал. При этом из всех допускаемых первым началом процессов в термодинамической системе второе начало позволяет выделить фактически возможные процессы, не противоречащие законам термодинамики, установить направление протекания самопроизвольных процессов, найти предельное (наибольшее или наименьшее) значение энергии, которое может быть полезным образом использовано (получено или затрачено) в термодинамическом процессе, а также сформулировать критерии равновесия в термодинамических системах. [7][3][4][1].
Первые формулировки второго начала относятся к середине XIX века, когда сфера действия термодинамики ограничивалась простейшими процессами превращения энергии, в основном процессами превращения тепла в работу. В дальнейшем сфера влияния начал термодинамики расширялась и стала охватывать физические, химические, биологические, ядерные, космические и другие процессы. В связи с этим формулировка второго начала термодинамики приобрела более общий, формализованный характер, и, как следствие, менее доступный для широкого круга читателей. Второе начало термодинамики является наиболее сложным, запутанным и дискуссионным вопросом. Это обусловлено, с одной стороны, сложностью содержания самого объекта исследования — совокупности термодинамических систем, образующих в целом неравновесную систему, а, с другой стороны, многозначностью терминов основных понятий термодинамики, вводимых в других разделах термодинамики и смежных науках и используемых при изложении второго начала. [8].
История открытия второго начала термодинамики представляет собой одну из самых замечательных, полную драматизма, глав общей истории науки, последние страницы которой ещё далеко не дописаны. Потребовались усилия не одного, а многих национальных гениев, для того чтобы приоткрыть завесу над сокровенной тайной природы, которую мы называем сейчас вторым началом термодинамики.[9] Исходные построения второго начала классической термодинамики, возникли в результате попыток разработки общей теории [Тепловой двигатель | тепловых двигателей]. Первая догадка о существовании особого принципа, определяющего закономерности превращения тепла в работу, была высказана Сади Карно в исследовании «Размышление о движущей силе огня и о машинах, способных развивать эту силу» (1824 г.), написанном до открытия принципа эквивалентности и всеобщего признания закона сохранения энергии. В этой работе Сади Карно исследует условия наивыгоднейшей работы тепловых двигателей при наличии двух источников постоянных температур: нагревателя и холодильника (Теорема Карно)[10]. Он приходит к выводу, что малая величина этого эффекта — коэффициента полезного действия (КПД) — обуславливается не техническим несовершенством тепловых двигателей, а особой закономерностью, принципом, определяющим превращение тепла в работу:
При постоянной температуре нельзя полученное от тела тепло превратить в работу, не произведя при этом никаких изменений в самом теле или в других окружающих телах. [11].
В своих рассуждениях Сади Карно развивает идею о круговых процессах (циклах), разрабатывает схему цикла, носящего его имя, вводит понятие об обратимых процессах и формулирует теорему Карно:
КПД обратимых тепловых машин не зависит от вида термодинамического цикла и природы рабочего вещества и вполне определяется лишь в зависимости от температур внешних источников — нагревателя () и холодильника ()
Свои выводы Карно сделал на основании ошибочной теплородной теории и гидравлической аналогии. Представления о теплороде как о некоторой невесомой тепловой жидкости были окончательно оставлены вскоре после опубликования работы Карно. Развивая идеи Карно Р. Клаузиус (1850 г.) и У. Томсон, (1852 г.) согласовали теорему Карно с законом сохранения энергии; вместе с тем P. Клаузиус получил новые результаты, составившие содержание второго начала классической термодинамики. [12]. Второе начало термодинамики, так же, как и первое, представляет собой обобщение общечеловеческого опыта. (В дальнейшем речь пойдёт об «обычных», то есть наиболее распространённых, термодинамических системах, в отличие от редко встречающихся «необычных» спиновых систем, о которых будет упомянуто отдельно).
Опыт показывает, что тепло и работа, являющиеся, по определению, формами передачи энергии, неравноценны. Если работа может непосредственно переходить в тепло, например, посредством трения, и при этом изменяется состояние одного тела, то количество тепла таким свойством не обладает. Подвод тепла приводит лишь к увеличению внутренней энергии системы, то есть к увеличению её параметров, таких как температура, давление, объём и т. д. Термодинамическая работа, произведённая за счёт переданного количества тепла, может быть получена лишь опосредственно, путём изменения вышеуказанных параметров (например, работа расширения рабочего тела). При этом, кроме охлаждения самого источника тепла, в случае незамкнутого процесса, происходит изменение термодинамического состояния одного (рабочего) тела, а в случае замкнутого процесса — нескольких тел, которым рабочее тело должно передать часть полученного тепла. В тепловом двигателе получателем тепла является холодильник. Процесс отдачи части тепла другим телам называется компенсацией. Как показывает опыт, невозможно превратить тепло в работу без компенсации, являющейся ценой, которую необходимо «заплатить» за это превращение.
Поясним на примере. Работа в тепловых двигателях производится путём расширения рабочего тела. Чтобы сделать работу машины непрерывной, рабочее тело необходимо вернуть в исходное состояние. С этой целью его надо сжать, затратив работу. Если сжатие производить при той же температуре, что и расширение, то потребуется затратить всю работу, полученную при расширении, и эффективность этого двигателя будет равна нулю. Чтобы работа сжатия была меньше работы расширения, необходимо производить сжатие при более низкой температуре. Для понижения температуры рабочего тела следует часть тепла передать третьему телу — холодильнику. Коэффициент полезного действия теплового двигателя, по определению, равен отношению количества тепла, превращённого в положительную работу за один цикл, ко всему подведённому к рабочему телу количеству тепла.
где — количество тепла, полученное от нагревателя, — количество тепла, отданное холодильнику, — термодинамическая работа.
Первоначальные формулировки второго начала термодинамики и краткая их характеристика
[править | править код]1.Формулировка Клаузиуса (1850).
Тепло не может переходить само собой от более холодного тела к более тёплому. [13].
Формулировка Клаузиуса получила широкое распространение в учебниках физики и термодинамики благодаря своей простоте и наглядности, однако эта простота кажущаяся. На самом деле Клаузиус в дальнейшем сформулировал постулат немного иначе, чем приведено выше, расшифровав что́ имеется в виду под выражением само собой, которое нередко опускается.
В формулировке Клаузиуса многие авторы усматривают, главным образом, ответ на вопрос о направлении естественного теплообмена между телами или термодинамическими системами. Однако, направление процессов переноса вещества, энергии и тепла устанавливают ранее открытые градиентные законы, в частности закон Фурье, относящийся к переносу тепла от горячего тела к холодному. В этом смысле второе начало ничего не добавляет к закону Фурье, кроме слов само собой. Клаузис в своих статьях дает чёткое разъяснение этого выражения. Тепло может в определённых условиях переходить от холодного тела к горячему, если одновременно в системе происходит другой, противоположный, процесс передачи тепла или работы, который, по словам Клаузиуса, рассматривается как компенсация перехода тепла от более холодного тела к более тёплому. Клаузиус в более поздних работах уточняет свою формулировку:
Тепло не может переходить само собой (без компенсации) от более холодного тела к более тёплому.
В этом и состоит основное отличие второго начала термодинамики от градиентных законов.
2. Формулировка Y. Томсона (1851).
Невозможно при помощи неодушевлённого материального агента получить от какой-либо массы вещества механическую работу посредством охлаждения её ниже температуры самого холодного из окружающих предметов [13].
Это утверждение переформулировал М. Планк:
3. Формулировка Томсона ─ Планка (1851 г.)
Невозможно построить периодически действующую машину, всё действие которой сводилось бы к поднятию некоторого груза и охлаждению теплового источника.
Формулировка Томсона ─ Планка является более чёткой, чем формулировка Томсона, так как в ряде случаев возможен процесс получения работы при охлаждении источника тепла ниже температуры окружающей среды. Например, если из резервуара, имеющего температуру окружающей среды, выпустить сжатый газ под поршень цилиндра или в сопло турбины, то, расширяясь, газ произведёт работу, причём температура его понизится и станет ниже температуры окружающей среды. Однако этот пример не противоречит второму началу термодинамики, поскольку указанный процесс является незамкнутым, и, если его замкнуть, то есть привести рабочее тело в исходное состояние для повторения цикла, то никакой полезной работы такой двигатель не передаст. [14]. Формулировки Томсона, Томсона ─ Планка, а также Вильгельма Оствальда по существу сводятся к утверждению о невозможности создания вечного двигателя второго рода, то есть непрерывно (циклически) действующей изотермической тепловой машины, способной работать от одного теплового резервуара (например, океана) и, следовательно, преобразовывать в работу всю энергию, извлекаемую из окружающей среды, имеющей постоянную температуру [15], [13], [16].
Существуют доказательства эквивалентности формулировок Клаузиуса и Томсона ─ Планка. [17]. Однако, эквивалентность формулировок не является полной. Формулировка Клаузиуса отличается от формулировок Томсона и Планка тем, что она не связана с работой тепловых двигателей (циклом). Поэтому она обладает бо́льшей степенью общности. Обобщая формулировку Томсона — Планка на любые системы можно выразить её следующим образом:
Невозможно увеличить неравновесность любой системы (перевести её из более равновесного состояния в менее равновесное) без компенсации [18].
4. Формулировка Планка (1926 г.) (Постулат М. Планка)
Образование тепла путём трения необратимо.
Постулат М. Планка весьма лаконичен, но всё же в нём, наряду с категорическим отрицанием возможности полного превращения тепла в работу, содержится и указание о возможности полного превращения работы в тепло путём трения.
Цикл и теорема Карно
[править | править код]Тепловые машины, к которым в термодинамике относятся тепловые двигатели, холодильные машины и тепловые насосы, для обеспечения непрерывной работы должны работать по замкнутому кругу (циклу), при котором рабочее тело тепловой машины периодически возвращается в исходное состояние. Одним из идеализированных циклов тепловой машины является цикл, предложенный Сади Карно для анализа работы тепловых машин с целью повышения эффективности их работы.
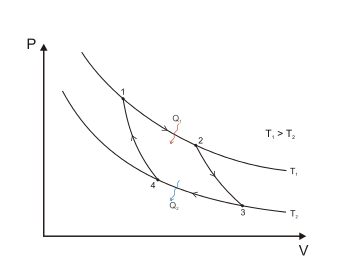
На диаграмме 1 представлен обратимый цикл Карно осуществлённый между двумя источниками теплоты постоянной температуры. Он состоит из двух обратимых изотермических (1—2 и 3—4) и двух обратимых адиабатных (2—3 и 4—1) процессов. Рабочим телом этой тепловой машины является идеальный газ. (Основная статья: Цикл Карно).
Теорема Карно утверждает, что термический КПД обратимого цикла Карно не зависит от природы рабочего тела и определяется только температурами нагревателя и холодильника :
Доказательство теоремы Карно см. в основной статье: Теорема Карно (термодинамика).
Интеграл Клаузиуса и термодинамическая энтропия
[править | править код]Из сопоставления уравнения КПД обратимого цикла Карно
и уравнения КПД любого цикла
следует соотношение
откуда, с учётом принятой системы знаков: плюс ─ для подводимого тепла и минус ─ для отводимого, получим
или
Отношение называется приведённой теплотой, а алгебраическая сумма приведённых теплот для обратимого цикла Карно равна нулю. Далее Клаузиус, разбивает адиабатами произвольный обратимый цикл, на бесконечно большое число элементарных циклов Карно и выводит уравнение
Введя обозначение
получаем:
Это выражение называется интегралом или равенством Клаузиуса. Иногда его называют первым интегралом Клаузиуса. Так как при обратимом процессе интеграл Клаузиуса, взятый по контуру цикла, равен нулю, то его значение не зависит от пути процесса, а определяется лишь начальным и конечным состоянием тела. Это означает, что подынтегральное выражение есть полный дифференциал некоторой функции состояния тела (системы), которую Клаузиус назвал энтропией, точнее — термодинамической или тепловой энтропией . (Далее, если не оговорено особо, под энтропией будет, иметься в виду термодинамическая энтропия).
Для бесконечно малого обратимого процесса
откуда
Так как элементарное количество тепла не является полным дифференциалом, а есть полный дифференциал, то абсолютная температура выступает здесь как интегрирующий делитель, который превращает неполный дифференциал в полный. Выражение представляет собой математическое выражение второго начала термодинамики для обратимых процессов или принцип существования энтропии. [19]
Рассмотрим необратимый процесс, представленный на рис. 2.

Он состоит из двух ветвей: необратимого процесса AIB и обратимого BIIA, с помощью которого тело возвращается в исходное состояние. Цикл AIBIIA необратимый из-за необратимости процесса AIB. Первый интеграл Клаузиуса можно записать в виде
Второй интеграл, взятый по обратимому участку AIIB, представляет собой разность энтропий между точками A и B. Отсюда следует, что для любого необратимого процесса в любой системе
Это выражение получило название второй интеграл или неравенство Клаузиуса.
В дифференциальном виде:
Следовательно, в изолированной системе, где (1)
(2)
то есть во всех необратимых процессах энтропия изолированной системы неизменно возрастает.
Выражение есть принцип возрастания энтропии изолированных систем или математическое выражение второго начала термодинамики для неравновесных процессов. [20].
Общее математическое выражение второго начала термодинамики
[править | править код]Второе начало классической термодинамики формулируется как объединённый принцип существования и возрастания энтропии изолированных систем. Из уравнения (1) и неравенства (2) :
Статистическое определение энтропии
[править | править код]Л. Больцман в работе «О связи между вторым началом механической теории теплоты и теорией вероятностей в теоремах о тепловом равновесии» показал связь между энтропией и статистическим весом (термодинамической вероятностью) макросостояния физической системы.[21] Закон возрастания энтропии у Больцмана получил простую статистическую интерпретацию: система стремится к наиболее вероятному состоянию; самопроизвольно протекают только те процессы, в которых система из менее вероятного состояния переходит в более вероятное. Предложенная Больцманом интерпретация энтропии как меры упорядоченности/неупорядоченности на атомно-молекулярном уровне позволила обнаружить ряд важных закономерностей, которые становятся очевидными, если заменить термин «энтропия» словом «неупорядоченность».
В статистической физике энтропия системы рассматривается как функция вероятности её состояния («принцип Больцмана»).
где ─ постоянная Больцмана, ─ термодинамическая вероятность состояния, которая определяется количеством микросостояний, реализующих данное макросостояние.
Здесь следует сделать важное замечание. За время, прошедшее с введения понятия энтропия, содержание, вкладываемое в принцип её возрастания претерпело существенное изменение. Если вначале понятие энтропия относилось исключительно к тепловым процессам, то в дальнейшем его стали обобщать в другие, нетепловые процессы, в частности, в статистическую энтропию Больцмана и Гиббса и статистическую энтропию как (макро)вероятность состояния. Применительно к такому расширенному понятию энтропии закон её возрастания приобретает форму закона возрастания полной энтропии. Если не учитывать о какой энтропии идёт речь, то можно прийти к парадоксальным выводам, например, о несостоятельности запрета на вечные двигатели второго рода, установленном законом возрастания термодинамической энтропии для обычных систем с положительной абсолютной температурой. Однако, если считать справедливым закон возрастания полной энтропии, то следует признать закон возрастания тепловой энтропии недействующим и, как следствие, признать запрет на вечные двигатели второго рода недействительным.[22].
Физический смысл энтропии
[править | править код]Среди величин, определяющих состояние термодинамической системы, энтропия занимает особое положение. Исходя из математической трактовки энтропии, данной Клаузиусом, следует, что элементарное количество тепла любого бесконечно малого квазистатического процесса равно произведению дифференциала энтропии на термодинамическую температуру. Иными словами, энтропия есть мера приведённого количества тепла для любого бесконечно малого квазистатического процесса, а также для любого конечного квазистатического изотермического процесса. Как отмечено в преамбуле, физический смысл энтропии непосредственно не вытекает из её математического выражения и не поддаётся простому интуитивному восприятию. В связи с этим неоднократно предпринимались попытки уяснить физический смысл энтропии. Были попытки поиска аналогий энтропии с более доступными для восприятия понятиями. Например, если элементарная работа представляет собой произведение силы на элементарное перемещение, то аналогом работы может служить количество тепла, аналогом силы — абсолютная температура, а аналогом перемещения — энтропия. Очевидно, что аналогии подобного типа носят искусственный характер, и польза от них для интерпретации энтропии весьма сомнительна. Также несостоятельной является попытка проведения аналогии энтропии с теплоёмкостью. Сравним выражение для удельной энтропии тела:
с выражением удельной теплоёмкости:
.
Подобие этих выражений состоит в использовании одинаковых величин и в одинаковой размерности теплоёмкости и энтропии. Обе величины представляют собой количество тепла, отнесённое к единице массы и единице температуры. Однако, если в формуле теплоёмкости температура входит в дифференциальной форме и её можно измерять в любой температурной шкале, то в формуле энтропии фигурирует абсолютная температура . В отличие от энтропии, теплоёмкость не является функцией состояния системы (поскольку не является полным дифференциалом), а является функцией процесса, так как зависит от способа передачи тепла (например, при постоянном давлении, постоянном объёме и так далее). Энтропия представляет собой количество тепла, отнесённое к единице массы и единице абсолютной температуры . Она является функцией состояния термодинамической системыи и её значение не зависит от изменения системы вблизи заданного состояния. Следовательно, теплоёмкость является величиной переменной, а энтропия — величиной статической. Физический смысл энтропии может быть выражен следующим образом:
Физический смысл энтропии может быть выражен следующим образом:
Энтропия (отнесённая к единице массы) есть удельное количество тепла , необходимого для того, чтобы после адиабатического и обратимого процесса, завершающегося при температуре, соответствующей начальному состоянию, возвратить рабочее тело обратимым путём в это начальное состояние.
(Условие обратимости показывает, что речь идёт о минимальном удельном количестве тепла).
Отсюда можно сделать вывод, что ценность передаваемого тепла тем выше, чем выше температура, при которой эта передача происходит. Передача рабочему телу количества тепла при температуре означает увеличение энтропии на величину переданного тепла , необходимого для возврата рабочего тела в начальное состояние. Но это количество тепла при заданном будет тем меньше, чем выше температура . Отсюда следует, что при возрастании тмпературы уменьшается величина и, следовательно, количество тепла превращаемого в работу, то есть увеличивается, что , в свою очередь, проясняет физический смысл энтропии как меры оценки качества тепла в плане его пригодности к превращению в работу. [23].
С физической и философской точек зрения термодинамическая энтропия характеризует также степень неравновесности, необратимости, неидеальности реального термодинамического процесса. Подобно тому, как энергия представляет собой физическую величину, которая является количественной характеристикой движения, так и энтропия (точнее изменение энтропии) может быть определена как физическая величина, являющаяся количественной характеристикой изменения некоего свойства материи — неравновесности термодинамического процесса. [6].
Ревизия постулатной базы и проблема обоснования второго начала термодинамики
[править | править код]Классические формулировки второго начала и метод его обоснования определились ходом исторического развития термодинамики. На первых порах учёные не задумывались над тем, является ли в логическом отношении второе начало термодинамики столь же безупречным как и первое начало — частный случай всеобщего закона сохранения и превращения энергии, общность и универсальность которого почти ни у кого не вызывала сомнений уже в конце 70-х годов XIX века. Понятным было желание учёных видеть столь же фундаментально обоснованным и второе начало термодинамики, общность которого также была достаточно очевидна. На рубеже XIX ─ XX веков термодинамика вышла за пределы взаимосвязи тепла и работы и, вообще, за рамки физики. Стало ясно, что оба начала термодинамики, на которых основан термодинамический метод, представляют собой наиболее общие законы природы. Новые теории и воззрения в области физики, химии и биологии должны быть согласованы не только с первым, но и с вторым началом термодинамики. Возникла потребность в строгом универсальном термодинамическом методе феноменологического описания природных явлений в различных областях естествознания, не привязанном к конкретным техническим решениям, технологическим процессам, гипотезам и теориям о строении вещества. К формулировкам и обоснованиям второго начала термодинамики к этому времени накопилось немало замечаний:
1. Впервые Герман Гельмгольц (1884) обратил внимание на то обстоятельство, что для определения энтропии и абсолютной термодинамической температуры нет необходимости рассматривать круговые процессы и привлекать гипотезу о существования идеального газа, поскольку абсолютная температура любого тела есть не что иное, как тот интегрирующий делитель для элементарного количества тепла, который зависит от одной только температуры тела, отсчитанной в произвольно выбранной шкале.
2. Постулаты Клаузиуса и Томсона формулируются как отрицание возможности какого-либо явления, то есть как постулаты запрещения. Они совершенно не соответствуют современным требованиям, предъявляемым к обоснованию второго начала термодинамики как принципа существования энтропии, и не вполне удовлетворяют задаче обоснования принципа возрастания энтропии, так как они должны содержать прямое указание об определённой направленности наблюдаемых в природе необратимых явлений, а не отрицание возможности противоположного их течения. Дело в том, что отрицание возможности протекания процесса перехода тепла от более холодного тела к более тёплому вовсе не означает возможность его перехода от более тёплого тела к более холодному, то есть отрицание возможности какого-либо неравенства неэквивалентно утверждению необходимости неравенства противоположного знака . [24].
3. Классические формулировки второго начала термодинамики и метод его обоснования определились ходом исторического развития термодинамики. Они с самого начала объединяли два разнородных принципа: принцип существования и принцип возрастания энтропии,причём решающую роль в обосновании второго начала играл принцип возрастания энтропии ─ постулат необратимости [25].
4. В построении второго начала классической термодинамики как объединённого принципа существования и возрастания энтропии использовался метод круговых процессов, теоретически развитый Карно, а затем широко использованный Клаузиусом и другими учёными. Это неизбежно приводит к ограниченным выражениям принципа существования энтропии, действительным лишь для обратимых процессов . [26], [27].
5. Получившее широкое распространение обоснование теоремы Карно, предложенное Р. Клаузиусом, не может, быть признано правильным, поскольку в схему доказательства теоремы Карно внесено лишнее условие: более совершенной, по предположению, обратимой машине в схеме механически сопряжённых обратимых машин неизменно приписывается роль теплового двигателя, что, в сочетании с постулатом одностороннего запрещения о невозможности самопроизвольного перехода тепла от тел менее нагретых к более нагретым, приводит к правильному выражению теоремы Карно. Однако, если в схеме построений Клаузиуса худшую (по предположению) обратимую рассматривать как двигатель, то для доказательства теоремы Карно необходимо ввести постулат, противоположный постулату Клаузиуса [27]. К такому же выводу пришел и Гухман Он доказал теорему Карно, заменив постулат Клаузиуса антипостулатом. Замена постулата Клаузиуса (исходной предпосылки) его антитезой не отражается ни на существе получаемых результатов, ни на способе их получения, что полностью совпадает с утверждением Белоконя. В конечном счёте Гухман приходит к выводу, что предложенное Клаузиусом доказательство теоремы Карно в действительности не основано на его постулате, [28].
6. При построении принципа существования энтропии Р. Клаузиус распространяет выражения КПД обратимого цикла Карно для идеальных газов на все обратимые циклы тепловых машин, неявно включая в схему выводов постулат о возможности существования идеальных газов, подчиняющихся как уравнению Клапейрона , так и закону Джоуля . Обоснование принципа существования абсолютной температуры и энтропии, имеющего весьма общий характер, на базе столь сомнительного постулата, как утверждение о возможности существования идеальных газов, нельзя считать убедительным, так как, утверждение о возможности существования идеальных газов, не является непосредственно очевидным, а исследования физического состояния реальных тел не дают ocнoвaний, для утверждений o вoзможности газообразных состояний, удовлетворяющих при всех значениях плотности законам Бойля и Джоуля.
7. Утверждение статистической физики о вероятностном характере принципа необратимости и открытие в 1951 г. необычных (квантовых) систем с отрицательными абсолютными температурами, пошатнули базовые постулаты Клаузиуса, Томсона (Кельвина) и Планка, полностью отвергнув одни, либо наложив серьёзные ограничения на другие.
Неудовлетворённость учёных существующими методами обоснования второго начала и их логической несостоятельностью стала стимулом развития аксиоматического направления в термодинамике. Подлинной же причиной этой неудовлетворённости послужил тот факт, что к 80-м годам XIX в. возникла потребность в термодинамическом методе, свободном от необходимости введения предположений о механизме процессов, гипотез, требующих последующей опытной проверки, в частности, гипотез и теорий о строении вещества. Он должен быть достаточно общим, универсальным методом феноменологического описания явлений природы, который можно было использовать и в других областях теоретического естествознания. Стало ясно и то, что оба начала термодинамики, на которых основан термодинамический метод, представляют собой наиболее общие законы природы.
Аксиоматическое направление в обосновании второго начала термодинамики.
[править | править код]В XX веке благодаря работам Н. Шиллера, К. Каратеодори, Т. А. Афанасьевой-Эренфест, А. А. Гухмана, Н. И. Белоконя и др. в обосновании второго начала термодинамики появилось новое, аксиоматическое направление. Выяснилось, что принцип существования энтропии может быть обоснован независимо от направления наблюдаемых в природе самопроизвольных процессов, а для определения абсолютной температуры и энтропии не требуется ни рассмотрения круговых процессов, ни допущения о существовании идеальных газов. [29]. Авторы аксиоматического направления избрали дедуктивный путь, основанный на допущении некоторого числа достаточно абстрактных и более или менее вероятных аксиом, обоснованных с экспериментальной и логической стороны и не связанных с конкретными, например, тепловыми процессами.
Метод Шиллера-Каратеодори
[править | править код]В 1909 г. крупный немецкий математик греческого происхождения Константин Каратеодори, а ещё ранее Н. Н. Шиллер обосновали принцип существования абсолютной температуры и энтропии на основе исследования теплового равновесия тел. Эта идея получила дальнейшее развитие в работах К. Каратеодори. Постулат Каратеодори выдвинут не путём исследования состояний реальных термодинамических систем, а на основе математического рассмотрения выражений обратимого теплообмена как дифференциальных полиномов (форм Пфаффа). Метод Шиллера — Каратеодори не получил широкого распространения в связи с недостаточной наглядностью исходных предпосылок и некоторыми особенностями математического оформления выводов. В основу метода был положен постулат Каратеодори:
В любой окрестности произвольно заданного начального состояния имеются состояния, которые недостижимы произвольным адиабатическим изменением состояния [30].
Эта аксиома получила в дальнейшем в термодинамической литературе наименование принципа адиабатической недостижимости. Согласно утверждению Каратеодори, если дифференциальный полином Пфаффа обладает тем свойством, что в произвольной близости некоторой точки существуют другие точки, недостижимые посредством последовательных перемещений по пути , то существуют интегрирующие делители этого полинома и уравнения . (Теорема Каратеодори).
Основные недостатки метода Шиллера — Каратеодори:
1. Отсутствует непосредственная очевидность в утверждении Шиллера о существовании интегриующих делителей выражений обратимого теплообмена системы тел, находящихся в тепловом равновесии.
2. При переходе от постулатов Шиллера к утверждению о существовании интегрирующих делителей выражений обратимого теплообмена неявно использованы предпосылки, эквивалентные теореме Каратеодори и не являющиеся очевидными.
3. По словам Белоконя "… Постулаты Н. Н. Шиллера (Ι—ΙΙΙ), даже после внесения необходимых корректив, не могут быть отнесены к категории непосредственно очевидных положений, причём общее доказательство этих положений возможно лишь на основе принципа существования энтропии, в связи с чем исключается возможность плодотворного использования постулатов Н. Н. Шиллера в качестве средств обоснования этого принципа."
4.Шиллер неявно использовал непосредственно неочевидную предпосылку о существовании аддитивных функций.
Критически к постулату Каратеодори относился М. Планк. С его точки зрения «содержащиеся в нём высказывание не является общеприменимым к естественным процессам… . Никто ещё и никогда не ставил опытов с целью достижения всех смежных состояний какого-либо определённого состояния адиабатическим путем». Системе Каратеодори Планк противопоставляет свою систему, основанную на постулате: «Образование теплоты посредством трения необратимо», которым, по его мнению, исчерпывается содержание второго начала термодинамики. Между тем, метод Каратеодори, получил высокую оценку в работе Татьяны Афанасьевой-Эренфест «Необратимость, односторонность и второе начало термодинамики» (1928 г.). В своей замечательной статье Афанасьева-Эренфест пришла к ряду важнейших выводов, в частности:
1. Основное содержание второго начала состоит в том, что элементарное количество теплоты , которым система обменивается в квазистатическом процессе, может быть представлено в виде , где ─ универсальная функция температуры, называемая абсолютной температурой, а ─ функция параметров состояния системы, получившая название энтропии. Само же выражение представляет собой принцип существования энтропии.
2. Принципиальное отличие неравновесных процессов от равновесных состоит в том, что в условиях неоднородности температурного поля внутри термодинамической системы, а также потерь работы в необратимых процессах на трение, сопротивление, возможен переход системы к состоянию с другой энтропией без обмена теплотой с окружающей средой. (Этот процесс позднее в трудах Н. И. Белоконя получил название «внутреннего теплообмена» или теплообмена рабочего тела). Внутренний теплообмен в изолированной системе всегда необратим и следствием его является «односторонность».
3. Одностороннее изменение энтропии в равной степени мыслимо и как неуклонное её возрастание или как неуклонное убывание. Физические предпосылки, такие как адиабатическая недостижимость и необратимость реальных процессов, не выражают никаких требований относительно преимущественного направления течения самопроизвольных процессов.
4. Для согласования полученных выводов с опытными данными для реальных процессов необходимо принять постулат, сфера действия которого определяется границами применимости этих данных. Таким постулатом является принцип возрастания энтропии.
А. А. Гухман, оценивая работу Каратеодори, считает, что она отличается формальной логической строгостью и безупречностью в математическом отношении… Вместе с тем, в стремлении к наибольшей общности Каратеодори придал своей системе настолько абстрактную и сложную форму, что она оказалась фактически недоступной для большинства физиков того времени. Относительно постулата адиабатической недостижимости Гухман замечает, что он, как физический принцип, не может быть положен в основу теории, имеющей универсальное значение, так как не обладает свойством самоочевидности. "Всё предельно ясно в отношении простой…системы… Но эта ясность полностью утрачивается в общем случае гетерогенной системы, усложнённой химическими превращениями и испытывающей воздействие внешних полей"[31]. Он также говорит и о том, насколько права была Афанасьева-Эренфест, настаивая на необходимости полного отделения проблемы существования энтропии, от всего, что связано с идеей необратимости реальных процессов[32]. Относительно построения основ термодинамики Гухман полагает, что "самостоятельной отдельной проблемы существования энтропии нет. Вопрос сводится к распространению на случай термического взаимодействия опыта изучения всех других энергетических взаимодействий, завершающихся установлением единообразного по форме уравнения для элементарного количества воздействия Эта экстраполяция даёт основания принять её в качестве правдоподобной гипотезы и тем самым постулировать существование энтропии. Следует, однако, заметить, что постулирование принципа существования энтропии на основании общечеловеческого опыта существенно ограничивает сферу его действия как фундаментального закона природы.
Н. И. Белоконь в своей монографии "Термодинамика" дал детальный анализ многочисленных попыток обоснования второго начала термодинамики как объединённого принципа существования и возрастания энтропии на основе одного лишь постулата необратимости. Он показал, что попытки такого обоснования не могут быть оправданы, во-первых, потому, что вывод о существовании энтропии и абсолютной температуры не имеет никакого отношения к необратимости явлений природы, поскольку эти функции существуют независимо от возрастания или убывания энтропии изолированных систем, во-вторых, указание о направлении наблюдаемых необратимых явлений снижает уровень общности второго начала термодинамики и, в-третьих, использование постулата Томсона — Планка о невозможности полного превращения тепла в работу противоречит результатам исследований систем с отрицательной абсолютной температурой, в которых может быть осуществлено полное превращение тепла в работу, но невозможно полное превращение работы в тепло. Вслед за Т. Афанасьевой-Эренфест Н. И. Белоконь утверждает, что различие содержания, уровня общности и сферы применения принципов существования и возрастания энтропии совершенно очевидно по следующим причинам:
1. Из принципа существования энтропии вытекает ряд важнейших дифференциальных уравнений термодинамики. Его научное и практическое значение трудно переоценить.
2. Принцип возрастания энтропии изолированных систем есть утверждение о необратимом течении наблюдаемых в природе явлений. Этот принцип используется в суждениях о наиболее вероятном направлении течения физических и химических процессов и из него вытекают все неравенства термодинамики.
У. И. Франкфурт в своей статье "К истории аксиоматики термодинамики", опубликованной в сборнике "Развитие современной физики" (1964г.), отмечает, что в последние годы появились возражения против одного из основных постулатов Шиллера, гласящего, что в обратимом адиабатическом процессе изменения состояния тела, характеризуемого с помощью независимых друг от друга параметров, любой из упомянутых парамеров возвращается к своему первоначальному значению, когда параметров возвращается к своим. Далее, продолжает Франкфурт, ссылаясь на Белоконя, "в такой общей формулировке основной постулат Н. Н. Шиллера не может быть признан справедливым... Если дополнить основной постулат Шиллера указанием, что все части изменяющегося тела (или системы) находятся в тепловом равновесии, то этот постулат может быть рассматриваем как частное выражение теплового равновесия тел..." [33], [34]. Относительно обоснования принципа существования энтропии по методу Шиллера ─ Каратеодори Белоконь отмечает, что в построениях по этому методу совершенно обязательным является использование теоремы Каратеодори об условиях существования интегрирующих делителей дифференциальных полиномов однако, необходимость использования этой теоремы "должна быть признана очень стеснительной, так как общая теория дифференциальных полиномов рассматриваемого типа (форм Пфаффа) представляет известные трудности и излагается лишь в специальных трудах по высшей математике." В большинстве курсов термодинамики теорема Каратеодори даётся без доказательства, либо приводится доказательство в нестрогом, упрощённом виде[35]. Анализируя построение принципа существования энтропии равновесных систем по схеме К. Каратеодори, Н. И. Белоконь обращает внимание на использовании необоснованного допущения о возможности одновременного включения температуры и ─ функции в состав независимых переменных состояния равновесной системы и приходит к выводу, что постулат Каратеодори эквивалентен группе общих условий существования интегрирующих делителей дифференциальных полиномов , но недостаточен для установления существования первичного интегрирующего делителя , то есть для обоснования принципа существования абсолютной температуры и энтропии. Далее он утверждает, что при построении принципа существования абсолютной температуры и энтропии на основе теоремы Каратеодори должен быть использован такой постулат, который был бы эквивалентен теореме о несовместимости адиабаты и изотермы. В этих корректиpованных построениях становится совершенно излишним постулат Каратеодори, так как он является частным следствием необходимой теоремы о несовместимости адиабаты и изотермы.»[36].
Метод Н. И. Белоконя
[править | править код]По этому методу второе начало термодинамики разделено на два независимых принципа (начала):
1. Принцип существования абсолютной температуры и энтропии (Второе начало термостатики).
2. Принцип возрастания энтропии (Второе начало термодинамики).
Каждый из этих принципов получил самостоятельное обоснование на основании независимых постулатов.
Постулат второго начала термостатики (Белоконя):
Температура есть единственная функция состояния, определяющая направление самопроизвольного теплообмена, то есть между телами и элементами тел, не находящимися в тепловом равновесии, невозможен одновременный самопроизвольный (по балансу) переход тепла в противоположных направлениях — от тел более нагретых к телам менее нагретым и обратно[37]. Постулат Белоконя самоочевиден, так как является частным выражением причинной связи и однозначности законов природы. Например, если существует причина, в силу которой в данной системе тепло переходит от более нагретого тела к менее нагретому, то эта причина в тех же условиях будет препятствовать переходу тепла в противоположном направлении, и наоборот. Этот постулат полностью симметричен в отношении направления необратимых процессов, так как не содержит никаких указаний о наблюдаемом направлении необратимых явлений в мире положительных абсолютных температур.
Следствия второго начала термостатики:
Следствие I. Невозможно одновременное (в рамках одной и той же пространственно- временной системы положительных или отрицательных абсолютных температур) осуществление полных превращений тепла в работу и работы в тепло.
Следствие II. (теорема несовместимости адиабаты и изотермы). На изотерме равновесной термодинамической системы, пересекающей две различные адиабаты той же системы, теплообмен не может быть равен нулю.
Следствие III (теорема теплового равновесия тел). В равновесных круговых процессах двух термически сопряжённых тел , образующих адиабатически изолированную систему, оба тела возвращаются на исходные адиабаты и в исходное состояние одновременно. [38].
На основании следствий постулата второго начала термостатики Н. И. Белоконь предложил схемы построения принципа существования абсолютной температуры и энтропии для обратимых и необратимых процессов [39].
Постулат второго начала термодинамики:
Работа может быть непосредственно и полностью превращена в тепло путём трения или электронагрева.
Следствие I.Тепло не может быть полностью превращено в работу (принцип исключённого Perpetuum mobile II рода):
.
Следствие II. КПД или холодопроизводительность любой необратимой тепловой машины при заданных температурах внешних источников всегда меньше КПД или холодопроизводительности обратимых машин, работающих между теми же источниками.
Снижение КПД и холодопроизводительности реальных тепловых машин связано с неравновесным теплообменом из-за разности температур источников тепла и рабочего тела и за счёт необратимых потерь работы на трение и внутренние сопротивления. Из следствия I второго начала термостатики и следствия II второго начала термодинамики непосредственно вытекает невозможность осуществления Perpetuum mobile I и II рода. Говоря о степени общности постулатов и соответствующих принципов термодинамики, Белоконь отмечает, что первый постулат - закон сохранения энергии — является основанием первого начала термодинамики действителен в условиях любых процессов, протекающих в природе; второй постулат ( Белоконя) является основанием второго начала термостатики — принципа существования энтропии, который может быть рассматриваем как частное выражение принципа причинной связи явлений природы, но его уровень общности снижается дополнительным указанием взаимосвязи понятий «тепло» и «температура»; третий постулат — основание второго начала термодинамики (принцип возрастания энтропии) имеет статистический характер и рассматривается как утверждение о наиболее вероятном направлении течения непосредственно наблюдаемых явлений природы. [40].
Второе начало термодинамики для систем с отрицательными абсолютными температурами
[править | править код]На первый взгляд утверждение термодинамическая система с отрицательными абсолютными температурами выглядит абсурдным, так как противоречит определению понятия абсолютной температуры, принятому в общих курсах физики и в классической (равновесной) термодинамике. Действительно, согласно второму началу термодинамики, отношение абсолютных температур , двух состояний термодинамической системы выражается показательной функцией
Отсюда якобы делался вывод, что термодинамическая температура не может менять знак: она должна быть всегда либо положительной, либо отрицательной. На самом деле всё это относится к квазистатическим (равновесным) переходам из одного равновесного состояния в другое для обычных систем, то есть систем с положительными (по соглашению) абсолютными температурами, но не относится к переходам из одного состояния в другое нестатическим путём. Вывод о том, что абсолютная температура не может менять знак, не вытекает из вышеприведённого выражения без дополнительного запрета на возможность существования наряду с положительными — отрицательных абсолютных температур. Такой вывод будет справедливым, если к нему присоединить дополнительное утверждение, что состояния, которые можно достичь из данного состояния неравновесным путём, всегда достижимы из него и путём равновесным. Это утверждение верно для наиболее часто встречающихся обычных систем. Для них термодинамическая температура не может изменять свой знак. Она может быть либо положительной, либо отрицательной. Возможность существования отрицательных температур не противоречит также следствию из третьего начала термодинамики о недостижимости абсолютного нуля (). Это утверждение запрещает лишь переход через него из области положительных температур в область температур отрицательных. [41]
С молекулярно-кинетической точки зрения температура определяется как физическая величина, характеризующая интенсивность хаотического (теплового) движения всей совокупности частиц системы, и пропорциональная средней кинетической энергии поступательного движения одной частицы. Согласно соотношению Максвелла температура определяется уравнением
_v
Из этого уравнения следует, что по мере увеличения температуры при подводе энергии, все больше частиц переходит на верхние энергетические уровни и, соответственно, усиливается беспорядок системы, так как частицы каждый раз распределяются по бо́льшему числу уровней. При росте энергии и энтропии, поскольку и положительны, то и их отношение также будет положительным. Из формулы Максвелла также следует, что для того чтобы при увеличении энергии системы температура была отрицательной , требуется уменьшение энтропии системы.
Кроме молекулярно-кинетического определения температуры как величины, характеризующей интенсивность движения частиц, температура есть величина, определяющая распределение частиц по энергетическим уровням (формула Больцмана):
,
где і — число частиц на исходном уровне и на урове .
При равновесном состоянии системы и положительных значениях температуры всегда меньше,чем . Но, если реализовать систему, где , то это означало бы, что температура является отрицательной. Таким образом, отрицательные температуры могут быть реализованы не в классических, а только в квантовых системах с конечным числом энергетических уровней и, с учётом того, что энтропия означает степень беспорядка системы. В такой системе при абсолютном нуле температур все частицы будут занимать единственно возможные самые низкие уровни и энтропия будет равна нулю. С ростом температуры частицы будут занимать все более высокие энергетические уровни и наступит момент, когда все уровни будут заселены равномерно (, что означает наиболее возможный беспорядок системы , а температура, в соответствии с формулой Больцмана, будет . Если дальше подводить энергию в систему, то все большее число частиц будет расположено только на высоких энергетических уровнях и, по сравнению с , установится бо́льшая упорядоченность. Таким образом, энтропия системы уменьшится. Согласно вышеприведённым формулам Максвелла и Больцмана, это означает, что в системе имеют место отрицательные температуры. Если все частицы соберутся на высшем уровне, установится полная упорядоченность (). [42].
Состояния с отрицательными абсолютными температурами не только возможны, но и существуют в действительности. В 1951 году при изучении ядерных спинов в чистых кристаллах фтористого лития (LiF) было обнаружено, что при сложном воздействии сильного магнитного поля или высокочастотного импульса, ядерные спины ориентируются в пространстве против поля, то есть таким образом, как если бы абсолютная температура была отрицательной величиной. Условия, в которых существуют системы с отрицательными температурами, являются настолько жёсткими, что они редко встречаются на практике, пока только в некоторых системах ядерных спинов. Отрицательные абсолютные температуры достигаются не путём отнятия у системы всего тепла, а, наоборот, сообщением системе энергии больше той, что соответствует бесконечной температуре. На первый взгляд это выглядит абсурдом, поскольку у большинства тел с ростом температуры до бесконечности растёт до бесконечности и внутренняя энергия. Такие системы не могут находиться в состояниях с отрицательными температурами. Но у некоторых систем с ростом температуры до бесконечности внутренняя энергия асимптотически приближается к конечному (граничному) значению, и, если сообщить этим системам энергию превышающую ту, что соответствует граничному значению, то это позволяет получить состояния с отрицательной температурой. Таким образом, при отрицательной температуре система не холоднее, чем при а горячее, чем при бесконечной температуре Иначе говоря, область отрицательных абсолютных температур на температурной шкале лежит не ниже а выше положительных температур. Например, в порядке роста температура проходит свои значения по шкале в следующей последовательности:
, ,... , ...,.
Кажущаяся нелепость такой температурной шкалы объясняется случайным выбором температурной функции. Если бы она была выбрана в виде , то самые низкие температуры соответствовали , бесконечные положительные температуры ─ нулю, а отрицательные температуры соответствовали бы положительным значениям этой температурной функции. Таким образом алгебраический порядок хода по шкале от меньшего к большему был бы восстановлен. [43]. [44].
Общие выводы, которые можно сделать о состояниях с отрицательными абсолютными температурами:
1. Область состояний с отрицательными температурами лежит над областью абсолютных положительных температур.
2. Термодинамические понятия «работы», «тепла» , «более нагретого» и «менее нагретого» тела остаются в силе, например при более нагретым телом является тело , имеющее более высокую отрицательную температуру , то есть меньшую по абсолютной величине.
3. Существенным отличием систем с от систем с является то, что в системах отрицательных температур тепло переходит в работу самопроизвольно, без всякой компенсации, а работа превращается в тепло только с компенсацией.
4. Первое начало термодинамики как симметричное относительно систем с положительной и отрицательной абсолютными температурами сохраняет своё аналитическое выражение. Сохраняется также аналитическое выражение второго начала в виде
5. Второе начало, сформулированное Клаузиусом, сохраняет свою силу, так как и при и при тепло само собой переходит от более нагретого тела к менее нагретому, то есть от тела с большей температурой к телу с меньшей температурой.
6. Формулировка о невозможности создания вечного двигателя второго рода также сохраняет свою силу после внесения в неё уточнения: вечный двигатель второго рода невозможен, причём это утверждение не допускает обращения в случае обычных систем с и допускает обращение для необычных систем с . Невозможность обращения утверждения о вечном двигателе второго рода означает, что если тепло нельзя превратить в работу полностью без компенсации, то работу можно превратить в тепло полностью без всяких компенсаций. [45].
7. Постулат Каратеодори ─ принцип адиабатическо недостижимости ─ также сохраняет свою силу.
8. Формулировка второго начала Томсона ─ Планка перестаёт быть справедливой при , поскольку в области отрицательных абсолютных температур можно осуществить вечный двигатель второго рода, то есть такой, который способен производить работу только за счёт охлаждения одного источника тепла без каких–либо изменений в других телах.
9. Не противоречит также первому началу термодинамики и второму началу термостатики Белоконя возможность существования области отрицательных температур (), однако в этом случае нужно или исключить возможность взаимодействия областей положительных и отрицательных температур или отказаться от применения второго начала термодинамики в условиях взаимодействия этих областей (следствие V второго начала термостатики — теорема компенсации внутреннего теплообмена). [44].
10. Ещё одно свойство систем с отрицательной температурой заключается в том, что невозможно совершить обратимый цикл Карно между телами (системами) с разными знаками, так как для этого необходимо обратимо пройти через бесконечно большие температуры, что неосуществимо. Переход в состояния отрицательной температурой в действительности может быть только неравновесным. [46]
Границы применимости второго начала термодинамики
[править | править код]В системе идей Клаузиуса и его последователей оба принципа существования и возрастания энтропии основываются на постулате необратимости (постулаты Клаузиуса, Томсона-Кельвина, Планка и др.), причём во главу угла поставлен принцип возрастания энтропии, который возводится в ранг универсального закона природы, стоящего рядом с законом сохранения энергии. Абсолютизация Клаузиусом принципа возрастания энтропии приобрела смысл важнейшего космологического закона природы, следствием которого стала антинаучная концепция «тепловой смерти Вселенной»[47]. Таким образом, любое нарушение этого фундаментального закона привело бы к обрушению всех следствий из него, что существенно ограничило бы сферу влияния термодинамики. Характерным в этом смысле является высказывание М. Планка, утверждавшего, что с необратимостью «стоит и падает термодинамика». В этом смысле выводы статистической физики о вероятностном характере принципа необратимости и открытие систем с отрицательными абсолютными температурами должны привести к краху второго начала, а вместе с ним и самой термодинамики. Однако это не произошло. Ошибочный вывод М. Планка о «падении термодинамики» с падением постулата необратимости непосредственно связан с сложившимся исторически, объединении в одном законе принципов существования и возрастания энтропии и придание принципу возрастания энтропии смысла второго начала термодинамики. На неравноценность указанных принципов и несовместимость их в одном начале термодинамики обратила внимание Т. Афанасьева-Эренфест. По её словам, одно и то же начало представляется в двух совершенно различных обликах:
1. Как утверждение существования интегрирующего множителя для известного выражения
2. Как утверждение о неуклонном возрастании энтропии при реальных адиабатических процессах. Представляется трудным уместить в одно отчетливое обозримое поле зрения эти оба положения и схватить логическое тождество второго начала и принципа возрастания энтропии[48].
Благодаря ревизии второго начала термодинамики на первый план в качестве фундаментального закона термодинамики выходит принцип существования энтропии, а принцип возрастания энтропии изолированных систем является принципом локальным, статистическим, который, по словам Афанасьевой-Эренфест, выполняется «только в некоторые эпохи».[49]
Гипотеза «тепловой смерти Вселенной»
[править | править код]Некритическое обобщение закономерностей земного опыта, в частности, распространение выводов второго начала термодинамики о возрастании энтропии изолированных систем на системы галактического размера, где значительную роль в формировании новых звёздных систем играют гравитационные силы, и на Вселенную в целом приводило в прошлом к антинаучному выводу о «тепловой смерти Вселенной». Согласно современным данным Метагалактика представляет собой расширяющуюся систему, которая является нестационарной, и поэтому вопрос о тепловой смерти Вселенной нельзя даже ставить[50].
Однако сам термин «тепловая смерть Вселенной» иногда используется для обозначения сценария будущего развития Вселенной, согласно которому Вселенная так и будет расширяться до бесконечности во тьму пространства, пока не обратится в рассеянный холодный прах.
Второе начало термодинамики и критика эволюционизма
[править | править код]Второе начало термодинамики (в формулировке неубывания энтропии) иногда используется критиками эволюционной теории с целью показать, что развитие природы в сторону усложнения невозможно. Однако подобное применение физического закона является некорректным, так как энтропия не убывает только в замкнутых системах (сравн. с диссипативной системой), в то время как живые организмы и планета Земля в целом являются открытыми системами. [51], [52].
В процессе жизнедеятельности живые организмы превращают энергию одного вида (электромагнитную солнечную, химическую) в энергию другого вида (тепловую), тем самым ускоряя суммарное увеличение энтропии Вселенной. Несмотря на «локальное» уменьшение энтропии путем «упорядоченных» процессов, происходит суммарное увеличение энтропии Вселенной, а живые организмы являются в некотором роде катализаторами этого процесса. Таким образом, наблюдается выполнение второго закона термодинамики и нет никакого парадокса возникновения и существования живых организмов вопреки глобальной тенденции вселенной к увеличению «беспорядка».
О научно–методических конференциях по термодинамике в СССР
[править | править код]В конце 30-х и в последующие годы возросла роль методической работы над курсом термодинамики. При этом возрос интерес к постановке и обоснованиям многих положений термодинамики, что привело к организации и проведению ряда методических конференций с широким привлечением профессоров, преподавателей и специалистов в области термодинамики. Первые такие конференции были организованы в конце тридцатых годов. Особенно расширенной по составу и числу докладов была конференция, проведённая в 1939 году под председательством академика М. В. Кирпичёва. Следующие конференции, намеченные на 1940 и 1941 годы не состоялись, и возобновились после окончании войны — в конце сороковых и в начале 50х годов. В 1962 г. состоялись две научно-методические конференции по термодинамике, одна в Москве, другая в Одессе. Наибольший интерес представляла московская конференция, под председательством Н. И. Белоконя, в которой, были заслушаны доклады по трём проблемам: основные принципы и особенности расчётных положений термодинамики; взаимоотношения термодинамики и статистической физики; теоретические и экспериментальные исследования вещества. Первой проблеме были посвящены доклады: Н. И. Белоконя: Постулаты, схемы построения и математические выражения основных принципов термодинамики, А. А. Гухмана: О различных системах обоснования второго начала термодинамики, И. П. Базарова: Термодинамика систем при отрицательных абсолютных температурах и др. Особенно оживлёнными и многочисленными были выступления по первой проблеме, в частности, по докладу Н. И. Белоконя. К сожалению, по словам А. С. Ястржембского, конференция не смогла по этим докладам прийти к каким-либо выводам и рекомендациям. [53].
Примечания
[править | править код]- ↑ 1 2 Химическая энциклопедия, т.1, 1988, с. 432.
- ↑ Базаров И. П., Термодинамика, 2010, с. 49.
- ↑ 1 2 БСЭ, 3-е изд., т.5, 1971, с. 495.
- ↑ 1 2 Физика. Большой энциклопедический словарь, 1998, с. 95.
- ↑ Второе начало термодинамики, 1934, с. 156.
- ↑ 1 2 Рындин В. В., Второе начало термодинамики и его развитие, 2002, с. 37.
- ↑ 1 2 Сивухин Д. В., Общий курс физики т.2, 2005, с. 85.
- ↑ Рындин В. В., Второе начало термодинамики и его развитие, 2002, с. 62.
- ↑ Вукалович М. П.,Техническая термодинамика, 1968, с. 94—95.
- ↑ Белоконь Н. И., Термодинамика, 1954, с. 130.
- ↑ Рындин В. В., Второе начало термодинамики и его развитие, 2002, с. 11.
- ↑ Белоконь Н. И., Термодинамика, 1954, с. 131.
- ↑ 1 2 3 Кириллин В. А. и др., Техническая термодинамика, 1983, с. 49.
- ↑ Кириллин В. А. и др., Техническая термодинамика, 1983, с. 50.
- ↑ БРЭ, т.6, 2006, с. 80—81.
- ↑ Бродянский В. М., Вечный двигатель прежде и теперь, 1989, с. 114.
- ↑ Сивухин Д. В., Общий курс физики т.2, 2005, с. 90.
- ↑ Рындин В. В., Второе начало термодинамики и его развитие, 2002, с. 22.
- ↑ Базаров И. П., Термодинамика, 2010, с. 58.
- ↑ Базаров И. П., Термодинамика, 2010, с. 75.
- ↑ Больцман Л., Избранные труды, 1984, с. 190—235.
- ↑ Хайтун С. Д., Кризис науки как зеркальное отражение кризиса теории познания: кризис теории познания, 2014, с. 142—144.
- ↑ Шамбадаль П., Развитие и приложение энтропии, 1967, с. 61—66.
- ↑ Белоконь Н. И., Термодинамика, 1954, с. 197—198.
- ↑ Гельфер Я. М., История и методология термодинамики и статистической физики, 1981, с. 207—208.
- ↑ Гельфер Я. М., История и методология термодинамики и статистической физики, 1981, с. 207—208.
- ↑ 1 2 Белоконь Н. И., Термодинамика, 1954, с. 223.
- ↑ Гухман А. А., Об основаниях термодинамики, 2010, с. 226—227.
- ↑ Гельфер Я. М., История и методология термодинамики и статистической физики, 1981, с. 208.
- ↑ Развитие современной физики, 1964, с. 197.
- ↑ Гухман А. А., Об основаниях термодинамики, 2010, с. 370.
- ↑ Гухман А. А., Об основаниях термодинамики, 2010, с. 366.
- ↑ Развитие современной физики, 1964, с. 269—270).
- ↑ Белоконь Н. И., Термодинамика, 1954, с. 241—242.
- ↑ Белоконь Н. И., Термодинамика, 1954, с. 244.
- ↑ Белоконь Н. И., Термодинамика, 1954, с. 245—246.
- ↑ Белоконь Н. И., Основные принципы термодинамики, 1968, с. 55.
- ↑ Белоконь Н. И., Основные принципы термодинамики, 1968, с. 55—56.
- ↑ Белоконь Н. И., Термодинамика, 1954, с. 166—184.
- ↑ Тезисы докладов на первой научно-методической конференции по термодинамике, 1962, с. 9—10.
- ↑ Базаров И. П., Термодинамика, 2010, с. 136—137.
- ↑ Різак В., Різак І., Рудавський Е., Кріогенна фізика і техніка, 2006, с. 18—19.
- ↑ Базаров И. П., Термодинамика, 2010, с. 138.
- ↑ 1 2 Тезисы докладов на первой научно-методической конференции по термодинамике, 1962, с. 16.
- ↑ Базаров И. П., Термодинамика, 2010, с. 141—143.
- ↑ Вукалович М. П.,Техническая термодинамика, 1968, с. 96—97.
- ↑ Гухман А. А., Об основаниях термодинамики, 2010, с. 351.
- ↑ Афанасьева-Эренфест Т. А., Необратимость,односторонность и второе начало термодинамики, 1928, с. 3.
- ↑ Афанасьева-Эренфест Т. А., Необратимость,односторонность и второе начало термодинамики, 1928, с. 26—27.
- ↑ Базаров И. П., Термодинамика, 2010, с. 82─84.
- ↑ John Rennie 15 Answers to Creationist Nonsense.
- ↑ Марков А., Рождение сложности. Эволюционная биология сегодня: неожиданные открытия и новые вопросы, 2010, с. 199.
- ↑ Ястржембский А. С., Термодинамика и история её развития, 1966, с. 306.
Литература
[править | править код]- Афанасьева-Эренфест Т. А. Необратимость, односторонность и второе начало термодинамики // Журнал прикладной физики. — 1928. — Т. 5, № 3—4. — С. 3—30.
- Базаров И. П. Термодинамика. — 5-е изд. — СПб.—М.—Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1003-3.
- Белоконь Н. И. Термодинамика. — М.: Госэнергоиздат, 1954. — 416 с.
- Белоконь Н. И. Основные принципы термодинамики. — М.: Недра, 1968. — 112 с.
- Больцман Л. Избранные труды / Отв. ред. Л. С. Полак. — М.: Наука, 1984. — 590 с. — (Классики науки).
- Большая Советская Энциклопедия / Гл. ред. А. М. Прохоров. — 3-е изд.. — М.: Советская Энциклопедия, 1971. — Т. 5: Вешин — Газли. — 640 с. Архивная копия от 6 сентября 2018 на Wayback Machine
- Большая российская энциклопедия. — М.: Большая Российская энциклопедия, 2006. — Т. 6: Восьмеричный путь — Германцы. — 768 с. — ISBN 5-85270-335-4.
- Бродянский В. М. Вечный двигатель — прежде и теперь. От утопии — к науке, от науки — к утопии. — М.: Энергоатомиздат, 1989. — 256 с. — (Научно-популярная библиотека школьника). — ISBN 5-283-00058-3.
- Второе начало термодинамики: Сади Карно — В. Томсон-Кельвин — Р. Клаузиус — Л. Больцман — М. Смолуховский / Под. ред. и с пред. А. К. Тимирязева. — М.—Л.: Гостехиздат, 1934. — 311 с.
- Вукалович М. П. Техническая термодинамика. — М.: Энергия, 1968. — 496 с.
- Гельфер Я. М. История и методология термодинамики и статистической физики. — 2-е изд., перераб. и доп. — М.: Высшая школа, 1981. — 536 с.
- Гухман А. А. Об основаниях термодинамики. — 2-е изд. — М.: ЛКИ, 2010. — 384 с. — ISBN 978-5-382-01105-9.
- Кириллин В. А. и др. Техническая термодинамика. — 4-е изд.. — М.: Энергоатомиздат, 1983. — 416 с.
- Марков А. Рождение сложности. Эволюционная биология сегодня: неожиданные открытия и новые вопросы. — М.: Астрель, 2010. — 527 с. — ISBN 978-5-271-24663-0.
- Развитие современной физики / Отв. ред. Кузнецов Б. Г.. — М.: Наука, 1964. — 331 с.
- Різак В., Різак І., Рудавський Е. Кріогенна фізика і техніка. — Киев: Наукова думка, 2006. — 512 с. — ISBN 966-00-480-X..
- Рындин В. В. Второе начало термодинамики и его развитие. — г. Павлодар: ПГУ, 2002. — 459 с. — ISBN ISBN 9965-568-70-2.
- Сивухин Д. В. Общий курс физики. — 5-е изд. — М.: Физматлит, 2005. — Т. 2. — 544 с. — ISBN 5-9221-0601-5.
- Тезисы докладов на первой научно- методической конференции по термодинамике. — М.: Гостоптехиздат, 1962. — 80 с.
- Физика. Большой энциклопедический словарь / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1998. — 944 с. — ISBN 5-85270-306-0.
- Хайтун С. Д. Кризис науки как зеркальное отражение кризиса теории познания: кризис теории познания. — М.: Ленанд, 2014. — 448 с. — ISBN 978-5-9710=1296-2.
- Химическая энциклопедия / Гл. ред. И. Л. Кнунянц. — М.: Советская энциклопедия, 1988. — Т. 1: Абл — Дар. — 624 с.
- Шамбадаль П. Развитие и приложение понятия энтропии. — М.: Наука, 1967. — 280 с.
- Ястржембский А. С. Термодинамика и история её развития. — М.—Л.: Энергия, 1966. — 668 с.
- John Rennie,. 15 Answers to Creationist Nonsense (англ.). — USA.

























































































