Эксперимент Кавендиша

Вертикальный разрез крутильных весов (рисунок 1 из статьи Кавендиша) с защищающей их конструкцией GGGG. ABCDDCBAEFFEA — неподвижный деревянный кожух, внутри которого подвешены крутильные весы, m — тонкий деревянный стержень коромысла, g — растяжка из тонкой серебряной проволоки, сообщающая жёсткость коромыслу, X — малые шары, подвешенные к коромыслу на проволоке, K — рукоятка механизма первоначальной установки коромысла, RrPrR — поворотная ферма, с закреплёнными на ней большими шарами W, MM — шкив поворотного механизма фермы, L — осветительные приборы, T — телескопы для наблюдения за отклонением коромысла через остеклённые отверстия в торцевых стенках кожуха, напротив концов коромысла.

Эксперимент Кавендиша — опыт, проведённый в 1797—1798 годах британским учёным Генри Кавендишем с целью определения средней плотности Земли, что впоследствии позволило вычислить её массу из радиуса Земли, определить массы Луны, Солнца и остальных планет Солнечной системы. Измерения плотности Земли с использованием маятников выполнялись до Кавендиша, но точность этих измерений была недостаточной. Хотя значение универсальной гравитационной постоянной также можно было определить по плотности Земли и в некоторых источниках оно приводится со ссылкой на Кавендиша, но в его статье значение указано не было.

Кавендиш усовершенствовал устройство, названное крутильными весами, разработанное примерно в 1783 году Джоном Мичеллом, который умер, не сумев завершить предложенный им эксперимент. Результат, полученный Кавендишем, заключался в том, что средняя плотность Земли составляла 5,437 г/см³, что всего на 1,4 % ниже принятого в настоящее время значения 5,515 г/см³. Использование крутильных весов для определения гравитационной постоянной или тестирования закона всемирного тяготения на малых расстояниях происходит и в современной истории, но с использованием всё более точных измерений.

Предыстория

Вулкан Чимборасо в Республике Эквадор.

Отклонение отвеса в районе горы.

Одна из первых попыток определения плотности Земли была предпринята профессором гидрографии Гавра французом Пьером Бугером во время геодезической миссии в Перу в 1735—1739 годы. Бугер провёл несколько экспериментов, чтобы определить взаимосвязь между плотностью вулкана Чимборасо и средней плотностью Земли, на основании отклонения от вертикали отвеса вблизи этой большой горы. Исаак Ньютон ранее рассматривал проведение эксперимента как практическую демонстрацию созданной им теории гравитации в своём сочинении «Начала», но в конце концов отверг эту идею. Результаты Бугера были не очень хорошими, так как одно измерение давало плотность Земли в четыре раза больше плотности горы, а другое в двенадцать раз больше.

Гора Шихаллион

Второй эксперимент по определению плотности Земли — это эксперимент Шихаллона середины 1774 года. В 1772 году комитет учёных из Лондонского королевского общества, в который входили Королевский астроном, преподобный Невил Маскелайн, Генри Кавендиш, Бенджамин Франклин, Дэйнс Баррингтон и преподобный Сэмюэл Хорсли, был убеждён, что они могут определить притяжение горы по отклонению отвеса, и летом 1773 года астроному Чарльзу Мейсону было поручено выбрать гору. Мейсон выбрал шотландскую гору Шихаллион в графстве Пертшир из-за её симметрии и изолированности. Эксперимент проводил Маскелайн, а данные обрабатывал Чарльз Хаттон. Окончательные результаты показали, что плотность Земли соответствует 4,500 г/см³, что на 20 % ниже принятого в настоящее время значения 5,515 г/см³.

Примерно в 1768 году преподобный Джон Мичелл, британский физик и геолог, также спроектировал и построил крутильные весы с целью определения средней плотности Земли. Этот прибор был похож на тот, который разработал француз Шарль Огюстен де Кулон, который использовал его для измерения небольших притяжений и отталкиваний электрических зарядов в 1784 году. Мичелл, похоже, не знал о работе Кулона, когда разрабатывал свои крутильные весы. Однако он умер, так и не сумев завершить придуманный им эксперимент, а построенный инструмент унаследовал преподобный Фрэнсис Джон Хайд Волластон, профессор натурфилософии Кембриджского университета, который передал его Генри Кавендишу; оба были членами Королевского общества.

Определение плотности Земли было важно в то время по нескольким причинам:

1. Оно бы усилило ньютоновскую физику, соединив принцип всемирного тяготения, объединивший небесную и земную механику, с геологией.
2. В области геологии, в конце XVIII века возникла полемика между двумя представлениями о внутреннем составе Земли: нептунианской теорией немца Авраама Готлоба Вернера, считавшего океан, воду, ответственными за образование минерального царства, и плутоновской теорией шотландца Джеймса Геттона, который приписывает основные земные геологические образования внутреннему теплу Земли. Следовательно, определение средней земной плотности позволило бы выяснить твёрдость или текучесть недр планеты.
3. Плотность Земли позволяла вычислить её массу, а это требовалось в астрономии восемнадцатого века, поскольку уже известные соотношения масс Луны, Солнца и остальных планет Солнечной системы можно было опеределить из этого значения.

Эксперимент

Генри Кавендиш

Генри Кавендиш начал свои эксперименты летом 1797 года в возрасте 67 лет в саду своего дома в Клэфэм-Коммон, ныне жилом районе на юге Лондона, где он поместил крутильные весы внутри комнаты здания размером 17,7×7,9 м. Первый эксперимент он провёл 5 августа 1797 года, и до 23 сентября провёл ещё семь опытов. Семь месяцев спустя, между 29 апреля и 30 мая 1798 года, он сделал ещё девять серий наблюдений, и последние два эксперимента — с помощью своего секретаря Джорджа Гилпина.

Обычно можно найти много книг, в которых ошибочно утверждается, что целью Кавендиша было определение гравитационной постоянной ${\textstyle G}$, и об этой ошибке сообщали несколько авторов. На самом деле единственной целью Кавендиша было определение плотности Земли, что он называл «взвешиванием мира». Гравитационная постоянная не фигурирует в оригинальной статье Кавендиша 1798 года «Эксперименты по определению плотности Земли» (англ. Experiments to Determine the Density of the Earth) и нет никаких указаний на то, что он рассматривал её определение как экспериментальную цель. Одно из первых упоминаний о ${\textstyle G}$, обозначенное как ${\textstyle f}$, появляется в 1844 году в 4-м издании книги Николя Дегена (фр. Nicolas Deguin) Cours élémentaire de Physique, но без написания полной формулы закона всемирного тяготения Ньютона. Впервые полная формула была написана в 1873 году в мемуарах Мари-Альфреда Корню и Баптистина Бая «Новое определение постоянной притяжения и средней плотности Земли» (фр. Détermination nouvelle de la constante de l'attraction et de la densité moyenne de la Terre) в виде:

$F=f\cdot {\frac {m\cdot m'}{r^{2}}}\,.$

Крутильные весы

Вид сверху на крутильные весы (рисунок 2 статьи Кавендиша). Схема горизонтального рычага с двумя маленькими сферами b и большими сферами в двух разных положениях (WW и ww).

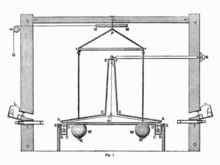
Крутильные весы Мичелла, перестроенные и улучшенные Кавендишем, состояли из нескольких частей:

Деталь крутильных весов (рисунок 1 статьи Кавендиша). W — толстая сфера, x — маленькая сфера. Деревянный ящик, закрывающий коромысло, — это ABCD. n представляет собой апертуру, через которую можно наблюдать градуированную шкалу h.

1. Горизонтальное деревянное коромысло незначительной массы и длиной 183 см (6 футов) было подвешено на тонкой проволоке длинной 102 см (40 дюймов) прямо посередине. На каждом конце коромысла находилась небольшая свинцовая сфера диаметром 5,08 см (2 дюйма) с массой 0,73 кг (b на рисунках). Всё заключено в ящик из красного дерева, АААА, для предотвращения сквозняков и перепадов температуры, с небольшими отверстиями на торцах, закрытыми стеклом, что позволяло наблюдать за положением этих сфер. Небольшая сила позволяла этому горизонтальному коромыслу вращаться вокруг оси вращения, отмеченной проволокой, если та была достаточно тонкой.
2. Рядом с каждой из вышеупомянутых сфер b у Кавендиша была ещё одна неподвижная сфера, также сделанная из свинца, но гораздо более тяжёлая, 158 кг (диаметром около 1 фута). Они указаны на рисунках в двух разных позициях, WW и ww. Чтобы разместить их очень близко к маленьким сферам, Кавендиш разработал механизм, который активирует их перемещение на расстоянии, чтобы избежать помех — отмечено как ММ. Гравитационное действие этих сфер должно было притягивать маленькие сферы к шарам на коромысле, производя небольшое закручивание проволоки.
3. Чтобы измерить отклонение малых сфер, Кавендиш расположил градуированную шкалу из слоновой кости внутри деревянного ящика, защищающего коромысло, расположенную рядом с маленькими сферами и освещённую лучом света снаружи. Шкала имела отдельные деления на расстоянии 0,13 см (1/20 дюйма). На конце коромысла находился небольшой кусочек слоновой кости, выполнявший роль шкалы нониуса и разделявший деления шкалы на 5 частей, то есть величиной около 0,25 мм. На многих схемах крутильных весов, встречающихся в литературе, указано, что несущая проволока имела зеркало, позволяющее наблюдать за производимым отклонением. Эта система является усовершенствованием, сделанным после эксперимента Кавендиша другими исследователями. Кавендиш измерял отклонение прямо на шкале возле маленьких сфер.
4. Для предотвращения возмущений, вызванных сквозняками и колебаниями температуры, Кавендиш поместил весы в закрытой комнате, на рисунке обозначенном вершинами GGGG. Большие сферы можно было перемещать из другой соседней комнаты с помощью механизма, обозначенного PRR, активируемого в точке m. И он мог также измерить небольшое кручение весов с помощью телескопа, отмеченного буквой Т, чтобы наблюдать отклонения на шкале из слоновой кости, освещённой светом от свечей, отмеченной буквой l.

Крутильные весы были удивительно точны для своего времени. Сила кручения, создаваемая притяжением шаров, была очень мала, 1,74 · 10⁻⁷ Н, что примерно равно 24 · 10⁻⁹ веса маленьких шаров. Эквивалентно силе, необходимой для удержания 0,0155 мг вещества. При подъёме песчинки диаметром 1 мм требуется усилие, примерно в 90 раз превышающее силу, измеренную по шкале Кавендиша.

Метод Кавендиша

Один конец современных крутильных весов, предназначенных для демонстрации эксперимента Кавендиша

Закон всемирного тяготения Ньютона гласит, что масса M притягивает другую массу m с силой F, пропорциональной произведению M · m и обратно пропорциональной квадрату расстояния r, разделяющего их.

Метод Кавендиша, используемый для расчёта плотности Земли, заключался в измерении периода колебаний горизонтального коромысла, которое колеблется, приближаясь к большой сфере и удаляясь от неё.

Когда большая сфера приближается на небольшое расстояние (9 дюймов или 22,9 см) к маленькой сфере, то сила гравитационного притяжения становится чувствительной и коромысло с маленькими сферами начинает вращаться в сторону больших сфер. По мере приближения малых сфер к более крупным сила притяжения увеличивается, так как она обратно пропорциональна расстоянию между их центрами, $F\propto 1/r^{2}\,$. В то же время это вызывает скручивание проволоки, поддерживающей коромысло, и возвращающую силу, противодействующую скручиванию. Эта рекуперативная сила увеличивается по мере приближения маленьких сфер к большим, поскольку она пропорциональна углу вращения (закон Гука), пока не сравняется с силой, которая их притягивает. В это время силы уравновешиваются, но коромысло с маленькими сферами обладает определённой скоростью (инерцией), что заставляет её продолжать движение в том же направлении. Однако сила возврата, противодействующая движению, становится больше, чем сила гравитационного притяжения, и успевает остановить движение коромысло. Таким образом, маленькие сферы останавливаются и меняют направление своего движения. Когда они снова проходят через положение равновесия, их скорость не равна нулю, что заставляет их продолжать движение. Сила кручения теперь действует в том же направлении, что и гравитационное притяжение, тормозя оба коромысла, и движение сфер медленно останавливается. Затем сферы начинают двигаться в противоположном направлении. То есть совершается колебательное движение, подобное движению простого маятника.

Период колебаний, измеренный Кавендишем, составил около 15 минут, что даёт представление о медленном движении коромысла. Кавендиш измерил время трёх полных колебаний, а затем определил период, разделив общее время на количество колебаний. Можно показать, что период связан с силой тяжести и силой восстановления проволоки. Колебание затухает и его амплитуда, не превышающая 2 см, несколько уменьшается при каждом колебании, хотя это и не влияет на не зависящий от него период. Чтобы полностью прекратить колебательное движение, потребовалось много часов, но вскоре Кавендиш изменил положение больших сфер на другой стороне и сумел реактивировать колебания и провести новые измерения.

Определив период этих малых колебаний, можно вычислить силу гравитационного притяжения малого шара со стороны большого шара известной массы М и сравнить её с силой притяжения такого же малого шара к Земле. Таким образом, Земля может быть описана как в N раз более массивная, чем толстая сфера. Все это основано на теории всемирного тяготения Исаака Ньютона, согласно которой сила притяжения пропорциональна произведению масс M и m и обратно пропорциональна квадрату расстояния r между ними

$F\propto {\frac {M\cdot m}{r^{2}}}\,.$

После того как были произведены расчёты и сделан ряд поправок, результат, полученный Кавендишем, состоял в том, что средняя плотность Земли в 5,448 раз превышала плотность воды при температуре от 19°С до 21°С (0,998 г/см³). Эта величина отличается всего на 1,4 % от принятого в настоящее время значения, что в 5,526 раз больше плотности воды, или 5,515 г/см³.

CAVENDISH, H. Experiments to Determine the Density of the Earth. Phil. Trans. R. Soc. Lond. 1 Gener 1798, 88:469-526

Несмотря на то, что опыт Кавендиша считается первым определением гравитационной постоянной, он не только не приводил её значение, но и не мог сослаться на закон всемирного тяготения в современной форме, потому, что до конца XIX века его так не записывали. В его время не существовало единства среди учёных в определении силы, периода колебаний и рассуждения велись используя сравнения и аналогии. Для математического анализа Кавендиш использовал аналогию крутильных весов с математическим маятником, период которого известен. Для математического маятника в крайнем положении возвращающая сила $F_{0}$ действует на вес груза $W$ и стремится вернуть его в положение равновесия. Длина дуги на которую сдвинут груз $S$ относится к длине подвеса $l$ как $F_{0}/W\,.$ Для математического маятника период равен $T_{0}\,.$ Он связан с периодом крутильного маятника $T$ под действием другой силы $F$ соотношением $F/F_{0}=T_{0}^{2}/T^{2}\,.$ С одной стороны возвращающая сила, действующая на крутильные весы запишется в виде $F=W\cdot S/l\cdot T_{0}^{2}/T^{2}$. Эксперимент позволил определить $F/T=B/(818T^{2})\,,$ где B — число делений шкалы крутильных весов. С другой стороны Кавендиш рассмотрел отношение притяжения двух свинцовых сфер к весу груза (то есть его притяжение к Земле). Вместо свинца он рассмотрел шар аналогичной массы из воды. Тогда ${\frac {F}{W}}=10,64\times 0,9779\times \left({\frac {6}{8,85}}\right)^{2}\left({\frac {D_{w}d_{w}^{3}}{d_{w}^{2}}}\right)\left({\frac {d_{e}^{2}}{D_{e}d_{e}^{3}}}\right)\,,$ где индексы $_{w}$ и $_{e}$ относятся к воде и Земле, $D$ — плотность, $d$ — диаметр, 10,64 — коэффициент разницы массы между шаром из свинца и шаром из воды радиусом 1 фут, 0,9779 — коэффициент, введённый для устранения ошибки в измерениях, а отношение 6/8,86 есть отношение радиуса сферы воды к расстоянию между центрами шаров в дюймах. Теперь можно выделить относительную плотность Земли, зная её диаметр (41800000 футов): $D={\frac {D_{e}}{D_{w}}}={\frac {818T^{2}}{8739000B}}$. Кавендиш провёл три измерения и взял среднее значение, которое оказалось неправильным из-за арифметической ошибки. Её исправил Бэйли и получил значение $D=5,448$.

Математическая формулировка

Схема крутильных весов Кавендиша. Установка измеряет силу притяжения между массами $M$ и $m$ для получения значения гравитационной постоянной $G.$ $(M)$ — масса неподвижных свинцовых шаров, $(m)$ — масса подвижных свинцовых шариков, $(F)$ — сила притяжения между каждой парой шариков, $(\theta )$ — угол закручивания упругой нити подвеса, $(\kappa )$ — коэффициент жёсткости торсионного подвеса, $(r)$ — расстояние между центрами шаров при закрученной нити подвеса, $(L)$ — расстояние между центрами маленьких шариков.

Определения терминов, используемых в формулах, приведены в подписи в конце этого раздела.

Приведённый ниже вывод формулы для определения плотности Земли использует современную терминологию. Он не соответствует методу, которому следовал Кавендиш.

Момент силы $\tau$, по определению является произведением силы на расстояние, отделяющее точку её приложения от оси вращения. Это соответствует произведению гравитационного притяжения между двумя сферами F и расстояния между каждой маленькой сферой и осью вращения коромысла, несущей две маленькие сферы, L/2. Так как имеются две пары сфер (2 большие и 2 маленькие) и каждая пара создаёт силу на расстоянии L/2 от оси весов, то момент силы равен 2·F·L/2 = F·L. В крутильных маятниках, как и в крутильных весах, момент силы $\tau$, пропорционален углу поворота $\theta$ весов, константой пропорциональности выступает коэффициент кручения, $\kappa$, это $\tau =\kappa \cdot \theta$. Таким образом, приравнивая обе формулы, получается следующее выражение:

$\kappa \cdot \theta \ =L\cdot F\,.\qquad \qquad \qquad (1)$

Сила гравитационного притяжения F между маленькой сферой массы m и большой сферой массы M, расстояние между центрами которых равно r, определяется выражением закона всемирного тяготения Исаака Ньютона:

$F=G\cdot {\frac {m\cdot M}{r^{2}}}\,.$

Подставив это выражение для F в уравнение (1), получается

$\kappa \cdot \theta \ =L\cdot G\cdot {\frac {m\cdot M}{r^{2}}}\,.\qquad \qquad \qquad (2)$

Для определения коэффициента крутящего момента $\kappa \,$, проволоки, можно измерить собственный период колебаний T крутильных весов, который выражается через момент инерции, I, и коэффициент кручения $\kappa$, согласно выражению

$T=2\cdot \pi \cdot {\sqrt {I/\kappa }}\,.\qquad \qquad \qquad (3)$

Учитывая, что масса деревянного коромысла пренебрежимо мала по сравнению с массами маленьких сфер, момент инерции весов обусловлен только двумя маленькими сферами и справедливо равенство:

$I=m\cdot (L/2)^{2}+m\cdot (L/2)^{2}=m\cdot L^{2}/2\,,$

где выражение (3) можно заменить и период примет вид

$T=2\cdot \pi \cdot {\sqrt {\frac {m\cdot L^{2}}{2\cdot \kappa }}}\,.$

Выразив из предыдущей формулы $\kappa$

$\kappa ={\frac {2\cdot \pi ^{2}\cdot m\cdot L^{2}}{T^{2}}}\,,$

в выражении (2) можно произвести замену и перестановку, выделив константу G:

$G={\frac {2\cdot \pi ^{2}\cdot L\cdot r^{2}}{M\cdot T^{2}}}\cdot \theta \,.\qquad \qquad \qquad (4)$

Притяжение, оказываемое Землёй на массу m (массу маленьких сфер), находящуюся вблизи её поверхности, то есть на её вес, составляет:

$m\cdot g=G\cdot {\frac {m\cdot M_{Terra}}{R_{Terra}^{2}}}\,.$

Выделяя массу Земли, получается выражение

$M_{Terra}={\frac {g\cdot R_{Terra}^{2}}{G}}\,.$

Подставляя значение G из периода колебаний, получаем массу Земли

$M_{Terra}={\frac {g\cdot R_{Terra}^{2}}{{\frac {2\cdot \pi ^{2}\cdot L\cdot r^{2}}{M\cdot T^{2}}}\cdot \theta }}={\frac {g\cdot R_{Terra}^{2}\cdot M\cdot T^{2}}{2\cdot \pi ^{2}\cdot L\cdot r^{2}\cdot \theta }}\,.$

Плотность Земли, $\rho _{Terra}$, это отношение её массы, $M_{Terra}$ к её объёму — объёму шара:

$\rho _{Terra}={\frac {M_{Terra}}{{\frac {4}{3}}\cdot \pi \cdot R_{Terra}^{3}}}\,.$

Легенда

Символ	Размерность	Определение
$\theta \,$	${\mbox{рад}}\,$	Угловое отклонение положения малых сфер относительно их положения равновесия
$F\,$	${\mbox{Н}}\,$	Гравитационная сила между массами M и m
$G\,$	${\mbox{м}}^{3}{\mbox{кг}}^{-1}{\mbox{с}}^{-2}\,$	Гравитационная постоянная
$m\,$	${\mbox{кг}}\,$	Масса маленьких сфер
$M\,$	${\mbox{кг}}\,$	Масса больших сфер
$r\,$	${\mbox{м}}\,$	Расстояние между центрами малых и больших сфер
$L\,$	${\mbox{м}}\,$	Расстояние между центрами двух маленьких сфер
$\kappa \,$	${\mbox{Н}}\,{\mbox{м}}\,{\mbox{рад}}^{-1}\,$	Коэффициент кручения проволоки
$I\,$	${\mbox{кг}}\,{\mbox{м}}^{2}\,$	Момент инерции коромысла
$T\,$	${\mbox{с}}\,$	Период колебаний коромысла
$g\,$	${\mbox{м}}\,{\mbox{с}}^{-2}\,$	Ускорение силы тяжести на поверхности Земли
$M_{Terra}\,$	${\mbox{кг}}\,$	Масса Земли
$R_{Terra}\,$	${\mbox{м}}\,$	Радиус Земли
$\rho _{Terra}\,$	${\mbox{кг}}\,{\mbox{м}}^{-3}\,$	Плотность Земли

Последующие эксперименты

После эксперимента Кавендиша другие учёные повторили эксперимент с той же сборкой, внося улучшения. С середины XIX века и далее проводились опыты с целью определения гравитационной постоянной ${\textstyle G}$, а не плотность Земли. Эти эксперименты имели следующие особенности:

• Немец Фердинанд Райх повторил измерение плотности Земли с помощью весов, очень похожих на те, которыми пользовался Кавендиш, и получил новые значения средней плотности Земли, ρ = 5,49 г/см³ в 1837 году и ρ = 5,58 г/см³ в 1852 году.
• Фрэнсис Бейли повторил эксперимент с крутильными весами и в 1842 году получил значение ρ = 5,67 г/см³. Его опыты финансировались правительством с целью улучшить измерения Кавендиша. Теория была построена Джорджем Эйри. В его опытах размеры, вес шаров и способ их подвеса варьировались.
• Французы Мари Альфред Корню и Баптистин Бай нашли в 1873 г. значения ρ в пределах от 5,50 до 5,56 г/см³.
• В 1895 году Чарльз Вернон Бойз модифицировал оригинальный инструмент Мичелла и Кавендиша, уменьшив его до 1/18 части, заменив торсионную проволоку, первоначально сделанную из железа, тонкими кварцевыми волокнами диаметром 0,002 мм. Это нововведение позволяет использовать меньшие массы золота (m = 2,7 г, M = 7,5 кг) и меньшее расстояние 15 см при лучшем контроле температурных колебаний и отклонений от уклона земли. Он также разделяет положение пар сфер на 6 дюймов по вертикали, чтобы уменьшить влияние толстой сферы другой пары, и имеет зеркало на плече, отражающее луч света, что позволило определить с помощью телескопа малый угол отклонения. Его измерения дали значение ρ = 5,527 г/см³.
• В 1897 году немецкий физик Карл Фердинанд Браун усовершенствовал крутильные весы, поместив их в контейнер, откуда он откачивал воздух, избегая таким образом сквозняков, влияющих на колебания. Он также использовал новый метод. Он расположил большие массы на одной линии с малыми массами коромысла, а затем изменил их расположение на 90°, способ, названный периодом колебаний. В положениях с четырьмя выровненными сферами гравитационное притяжение сокращает период колебаний и удлиняет массы в скрещённых, более удалённых положениях. У него получилось значение ρ = 5,527 г/см³, как и у Бойза.
• Метод Брауна также был использован в 1930 году Паулем Ренно Хейлом с различными материалами (золото, платина и стекло) и получил среднее значение плотности Земли ρ = 5,517 г/см³. Он повторил эксперимент в 1942 году вместе с Петером Хшановски, и получили значение ρ = 5,514 г/см³, проводя эксперимент с разными проволоками. Наконец, Габриэль Г. Лютер и Уильям Р. Таулер в 1982 г. использовали вольфрамовые сферы массой 10,5 кг и получили очень точное значение.
• В 2008—2010 годах были опубликованы результаты ещё трёх экспериментов. Хотя авторы каждого из них заявляют о высокой точности полученного значения, их результаты различаются на величину больше заявленных экспериментальных погрешностей.
• В 2021 году эксперимент был повторён на золотых шариках диаметром 2 мм и массой всего 90 мг. Сила, действующая между ними, не превышала 10⁻¹³ Н.

Год	Экспериментаторы	Описание	Плотность Земли, г/см³	Гравитационная постоянная, 10−11 м³/(кг·с²)
1837—1847, 1852	Ф. Райх	Провёл две серии опытов.	5,58	6,70±0,04
1843	Ф. Бейли	Было проведено 2000 опытов	5,6747±0,0038.	6,63±0,07
1873	А. Корню и Ф. Бейли	При помощи более совершенного прибора, составленного из алюминиевого стержня, маленьких платиновых шариков и больших стеклянных шаров, наполненных ртутью	5,50—5,58.	6,64±0,017
1880	Ф. Йолли	Использовал обыкновенные рычажные весы.	5,692 ± 0,068	6,58
1887	И. Вильзинг	Вместо горизонтального стержня, отклоняемого тяжёлыми шарами в опытах Кавендиша, он использовал вертикальный.	5,594 ± 0,032	6,71
1895	Ч. Бойс	Улучшил измерения уменьшив размер установки.	5,5270	6,66 ± 0,007
1930	П. Хейл		5,517	6,670 ± 0,005
1942	П. Хейл и П. Хржановский		5,514	6,673 ± 0,003
1982	G. Luther и W. Towler		5,617	6,6726 ± 0,0005
2000	Университет Вашингтона в Сиэтле		5,6154	6,67390
2018	CODATA			6,674 30(15)

Ссылки

• Angel Franco Garcia. La experiencia de Cavendish (исп.) (2010). Дата обращения: 23 января 2022.
• John W. Dooley. Sideways Gravity in the Basement: Norman Scheinberg's Cavendish Experiment (англ.) (1 июля 2005). Архивировано из оригинала 5 июля 2008 года. Самодельный эксперимент Кавендиша, показывающий расчёт результатов и необходимые меры предосторожности для устранения ошибок из-за электростатических зарядов и ветра
• Big 'G' (англ.). https://www.physicscentral.com/. PhysicsCentral (2000). Дата обращения: 23 января 2022. Эксперимент в университете Вашингтона для измерения «G» с использованием варианта метода Кавендиша