Метод Гаусса
Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Назван в честь немецкого математика Карла Фридриха Гаусса. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы[1].
История[править | править код]
Хотя в настоящее время данный метод повсеместно называется методом Гаусса, он был известен и до К. Ф. Гаусса. Первое известное описание данного метода — в китайском трактате «Математика в девяти книгах».
Описание метода[править | править код]
Пусть исходная система выглядит следующим образом:
Её можно записать в матричном виде:
где
Матрица называется основной матрицей системы, — столбцом свободных членов.
Тогда, согласно свойству элементарных преобразований над строками, основную матрицу этой системы можно привести к ступенчатому виду (эти же преобразования нужно применять к столбцу свободных членов):
где
При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных [2].
Тогда переменные называются главными переменными. Все остальные называются свободными.
Если хотя бы одно число , где , то рассматриваемая система несовместна, т. е. у неё нет ни одного решения.
Пусть для любых .
Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом (, где — номер строки):
- ,
где
Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.
Критерий совместности[править | править код]
Упомянутое выше условие для всех может быть сформулировано в качестве необходимого и достаточного условия совместности:
Напомним, что рангом совместной системы называется ранг её основной матрицы (либо расширенной, так как они равны).
| Теорема Кронекера — Капелли. Система совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы. Следствия:
|
Алгоритм[править | править код]
Блок-схема представлена на рисунке. Данный рисунок — адаптированный для написания программы на языке C/C++, где a — расширенная матрица, последний столбец в которой — столбец свободных членов. Количество строк — n.
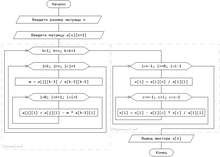
Описание[править | править код]
Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа.
- На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. Для этого среди элементов первого столбца матрицы выбирают ненулевой, перемещают содержащую его строку в крайнее верхнее положение, делая эту строку первой. Далее ненулевые элементы первого столбца всех нижележащих строк обнуляются путём вычитания из каждой строки первой строки, домноженной на отношение первого элемента этих строк к первому элементу первой строки. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают, пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.
- На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.
Метод Гаусса требует арифметических операций.
Этот метод опирается на:
| Теорема (о приведении матриц к ступенчатому виду). Любую матрицу путём элементарных преобразований только над строками можно привести к ступенчатому виду. |
Простейший случай[править | править код]
В простейшем случае алгоритм выглядит так:
- Прямой ход:
- Обратный ход. Из последнего ненулевого уравнения выражаем базисную переменную через небазисные и подставляем в предыдущие уравнения. Повторяя эту процедуру для всех базисных переменных, получаем фундаментальное решение.
Пример[править | править код]
Покажем, как методом Гаусса можно решить следующую систему:
Обнулим коэффициенты при во второй и третьей строчках. Для этого прибавим к ним первую строчку, умноженную на и , соответственно:
Теперь обнулим коэффициент при в третьей строке, вычтя из неё вторую строку, умноженную на :
В результате мы привели исходную систему к треугольному виду, тем самым закончив первый этап алгоритма.
На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:
- из третьего;
- из второго, подставив полученное
- из первого, подставив полученные и .
Таким образом, исходная система решена.
В случае, если число уравнений в совместной системе получилось меньше числа неизвестных, то тогда ответ будет записываться в виде фундаментальной системы решений.
Реализация алгоритма на языке программирования C#[править | править код]
namespace Gauss_Method
{
class Maths
{
/// <summary>
/// Метод Гаусса (Решение СЛАУ)
/// </summary>
/// <param name="Matrix">Начальная матрица</param>
/// <returns></returns>
public static double[] Gauss(double[,] Matrix)
{
int n = Matrix.GetLength(0); //Размерность начальной матрицы (строки)
double[,] Matrix_Clone = new double[n, n + 1]; //Матрица-дублер
for (int i = 0; i < n; i++)
for (int j = 0; j < n + 1; j++)
Matrix_Clone[i, j] = Matrix[i, j];
// Прямой ход (Зануление нижнего левого угла)
for (int k = 0; k < n; k++) //k-номер строки
{
for (int i = 0; i < n + 1; i++) //i-номер столбца
Matrix_Clone[k, i] = Matrix_Clone[k, i] / Matrix[k, k]; //Деление k-строки на первый член !=0 для преобразования его в единицу
for (int i = k + 1; i < n; i++) //i-номер следующей строки после k
{
double K = Matrix_Clone[i, k] / Matrix_Clone[k, k]; //Коэффициент
for (int j = 0; j < n + 1; j++) //j-номер столбца следующей строки после k
Matrix_Clone[i, j] = Matrix_Clone[i, j] - Matrix_Clone[k, j] * K; //Зануление элементов матрицы ниже первого члена, преобразованного в единицу
}
for (int i = 0; i < n; i++) //Обновление, внесение изменений в начальную матрицу
for (int j = 0; j < n + 1; j++)
Matrix[i, j] = Matrix_Clone[i, j];
}
// Обратный ход (Зануление верхнего правого угла)
for (int k = n - 1; k > -1; k--) //k-номер строки
{
for (int i = n; i > -1; i--) //i-номер столбца
Matrix_Clone[k, i] = Matrix_Clone[k, i] / Matrix[k, k];
for (int i = k - 1; i > -1; i--) //i-номер следующей строки после k
{
double K = Matrix_Clone[i, k] / Matrix_Clone[k, k];
for (int j = n; j > -1; j--) //j-номер столбца следующей строки после k
Matrix_Clone[i, j] = Matrix_Clone[i, j] - Matrix_Clone[k, j] * K;
}
}
// Отделяем от общей матрицы ответы
double[] Answer = new double[n];
for (int i = 0; i < n; i++)
Answer[i] = Matrix_Clone[i, n];
return Answer;
}
}
}
Применение и модификации[править | править код]
Помимо аналитического решения СЛАУ, метод Гаусса также применяется для:
- нахождения матрицы, обратной к данной (к матрице справа приписывается единичная такого же размера, что и исходная: , после чего приводится к виду единичной матрицы методом Гаусса—Жордана; в результате на месте изначальной единичной матрицы справа оказывается обратная к исходной матрица: );
- определения ранга матрицы (согласно следствию из теоремы Кронекера — Капелли ранг матрицы равен числу её главных переменных);
- численного решения СЛАУ в технических приложениях (для уменьшения погрешности вычислений используется Метод Гаусса с выделением главного элемента, суть которого заключена в том, чтобы на каждом шаге в качестве главной переменной выбирать ту, при которой среди оставшихся после вычёркивания очередных строк и столбцов стоит максимальный по модулю коэффициент).
Достоинства метода[править | править код]
- Для матриц ограниченного размера — менее трудоёмкий по сравнению с другими методами.
- Позволяет однозначно установить, совместна система или нет, и если совместна, найти её решение.
- Позволяет найти максимальное число линейно независимых уравнений — ранг матрицы системы[3].
Устойчивость метода Гаусса[править | править код]
Метод Гаусса для плохо обусловленных матриц коэффициентов является вычислительно неустойчивым. Например, для матриц Гильберта метод приводит к очень большим ошибкам даже при небольшой размерности этих матриц. Уменьшить вычислительную ошибку можно с помощью метода Гаусса с выделением главного элемента, который является условно устойчивым[4]. Широкое применение метода Гаусса связано с тем, что плохо обусловленные матрицы встречаются на практике относительно редко.
Неоптимальность метода Гаусса[править | править код]
В 1969 году Штрассен доказал, что большие матрицы можно перемножить за время [5]. Отсюда вытекает, что обращение матриц и решение СЛАУ можно осуществлять алгоритмами асимптотически более быстрыми по порядку, чем метод Гаусса. Таким образом, для больших СЛАУ метод Гаусса не оптимален по скорости.
См. также[править | править код]
- Метод Гаусса — Жордана
- Метод Крамера
- Система линейных алгебраических уравнений
- Теорема Кронекера — Капелли
- Фундаментальная система решений
- Элементарные преобразования матрицы
- Метод Гаусса (оптимизация)
- Метод покоординатного спуска (Гаусса — Зейделя)
- Метод Якоби
Примечания[править | править код]
- ↑ Н. Ш. Кремер, 2.3. «Метод Гаусса», стр. 44
- ↑ Такого расположения минора можно добиться перестановкой столбцов основной матрицы и соответствующей перенумерацией переменных.
- ↑ Н. Ш. Кремер, 2.4. «Система m линейных уравнений с n переменными», стр. 49
- ↑ УСТОЙЧИВОСТЬ И ТОЧНОСТЬ ПРЯМЫХ МЕТОДОВ (недоступная ссылка)
- ↑ Strassen V. Gaussian Elimination is not Optimal (англ.) // Numerische Mathematik / F. Brezzi — Springer Science+Business Media, 1969. — Vol. 13, Iss. 4. — P. 354—356. — ISSN 0029-599X; 0945-3245 — doi:10.1007/BF02165411
Литература[править | править код]
- И. М. Виноградов. Гаусса метод // Математическая энциклопедия. — М.: Советская энциклопедия. — 1977—1985.
- Ильин В. А., Позняк Э. Г. Линейная алгебра: Учебник для вузов. — 6-е изд., стер. — М.: ФИЗМАТЛИТ, 2004. — 280 с.
- Амосов А. А., Дубинский Ю. А., Копченова Н. П. Вычислительные методы для инженеров. — М.: Мир, 1998.
- Бахвалов Н. С., Жидков Н. П., Кобельков Г. Г. Численные методы. — 8-е изд. — М.: Лаборатория Базовых Знаний, 2000.
- Волков Е. А. Численные методы. — М.: Физматлит, 2003.
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1970. — С. 575—576.
- Кремер Н. Ш., Путко Б. А., Тришин И. М., Фридман М. Н. Высшая математика для экономистов / Под ред. Н. Ш. Кремера. — 3-е изд. — М.: ЮНИТИ-ДАНА, 2007. — 479 с. — ISBN 5-238-00991-7.
Ссылки[править | править код]
- Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Section 2.2", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8






























![{\displaystyle [A|E]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b6bf5ec2ef6d945c24786cfc8038f7679a7ac5f)
![{\displaystyle [E|A^{-1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b7dd222f98d4db05cfd9c4494966fbbeb1a6061)
