Букет окружностей
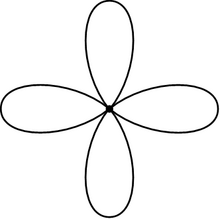
Букет окружностей (известный также как роза) — это топологическое пространство, полученное путём склеивания набора окружностей вокруг одной точки. Окружности букета иногда называются лепестками розы. Букеты окружностей важны в алгебраической топологии, где они тесно связаны со свободными группами.
Определение[править | править код]

Букет окружностей является частным случаем букета пространств. То есть букет окружностей является факторпространством C/S, где C является несвязным объединением окружностей по множеству S, состоящему по одной точке из каждой окружности. Как клеточный комплекс букет окружностей имеет одну вершину и по одному ребру для каждой окружности. Это делает его простым примером топологического графа.
Букет из n окружностей может быть получена также путём отождествления n точек одной окружности. Букет из двух окружностей называется восьмёркой.
Связь со свободными группами[править | править код]

Фундаментальная группа букета окружностей является свободной с одним генератором для каждого лепестка. Универсальное накрытие является бесконечным деревом, которое может быть отождествлён с графом Кэли свободной группы. (Это специальный случай комплекса презентаций[англ.], ассоциированного с любым заданием группы.)
Промежуточные накрытия букета окружностей соответствуют подгруппам свободной группы. Наблюдение, что любое накрытие букета окружностей является графом, даёт простое доказательство, что любая подгруппа свободной группы свободна (теорема Нильсена — Шрейера[англ.]).
Поскольку универсальное накрытие букета окружностей стягиваемо, букет окружностей является K(F,1) пространством для ассоциированной свободной группы F. Из этого следует, что когомология групп[англ.] тривиальна для .
Другие свойства[править | править код]

- Любой связный граф гомотопически эквивалентен букету окружностей. В частности, букет окружностей является факторпространством графа, полученного путём стягивания остовного дерева.
- Шар с удалёнными n точками (или сфера с удалёнными точками) является деформационным ретрактом в букет окружностей с n лепестками. Одна из окружностей букета окружает каждую из удалённых точек.
- Тор с одной удалённой точкой является деформационным ретрактом в восьмёрку, а именно объединением двух генерирующих окружностей. Более обще, поверхность рода g с одной удалённой точкой является деформационным ретрактом в букет окружностей с 2g лепестками, а именно в границу фундаментального многоугольника[англ.].
- Букет окружностей может иметь бесконечно много лепестков, что приводит к фундаментальной группе, которая свободна на бесконечно большом числе генераторов. Букет из счётного числа окружностей подобен гавайской серьге — имеется непрерывная биекция из букета окружностей в гавайскую серьгу, но они не гомеоморфны.
См. также[править | править код]
- Букет (граф)[англ.]
- Квадрифолий (четырёхлистник)
- Свободная группа
- Топологический граф
Примечания[править | править код]
Литература[править | править код]
- Allen Hatcher. Algebraic topology. — Cambridge, UK: Cambridge University Press, 2002. — ISBN 0-521-79540-0.
- James R. Munkres. Topology. — Englewood Cliffs, N.J: Prentice Hall, Inc, 2000. — ISBN 0-13-181629-2.
- John Stillwell. Classical topology and combinatorial group theory. — Berlin: Springer-Verlag, 1993. — ISBN 0-387-97970-0.


