База данных шахматных окончаний
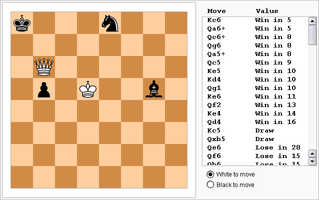
База данных шахматных окончаний — компьютеризированная база данных, содержащая предварительно рассчитанный исчерпывающий анализ шахматных эндшпилей. В такой базе данных хранятся оценки (выигрыш, ничья, поражение) для каждой возможной позиции шахматного окончания как при ходе белых, так и при ходе чёрных[1]. Некоторые распространённые базы данных также содержат количество ходов, необходимых для достижения теоретического результата (мат, переход в младший выигранный эндшпиль и т. п.) при наилучшей игре обеих сторон. Базы данных шахматных окончаний создаются путём ретроспективного анализа, двигаясь от всех возможных заключительных позиций в обратном направлении — в сторону увеличения количества ходов, необходимых для достижения этих заключительных позиций.
Таблицы Налимова[править | править код]
В компьютерных шахматах одним из наиболее популярных форматов баз данных шахматных окончаний являются эндшпильные таблицы Налимова. Эта база данных (состоящая из множества отдельных файлов-таблиц) названа именем новосибирского программиста Евгения Налимова, который предложил эффективный алгоритм для генерации эндшпильных баз данных. В таблицах Налимова имеются абсолютно точные варианты развития шахматной партии в эндшпиле. С помощью таблиц Налимова определяются все возможные варианты продолжения игры, все возможные результаты и число ходов, через которое при оптимальной игре партия придёт к мату слабейшей стороне[2].
Почти все современные компьютерные программы для игры в шахматы имеют опцию для подключения таблиц Налимова.
Длиннейшие выигрыши[3][править | править код]
| Количество фигур | Мат в Х ходов | FEN |
|---|---|---|
| 3-фигурные окончания. | 28 | 8/8/8/1k6/8/8/K5P1/8 w - - 0 1 |
| 4-фигурные окончания. | 43 | 8/5k2/2PK4/5r2/8/8/8/8 w - - 0 1 |
| 5-фигурные окончания. | 127 | 8/8/8/8/1p2P3/4P3/1k6/3K4 w - - 0 1 |
| 6-фигурные окончания. | 262 | 6k1/5n2/8/8/8/5n2/1RK5/1N6 w - - 0 1 |
| 7-фигурные окончания. | 549 | 1n1k4/6Q1/5KP1/8/7b/1r6/8/8 w - - 0 1 |
| 8-фигурные окончания. | 584[4] | R7/8/8/8/7q/2K1B2p/7P/2Bk4 w - - 0 1 |
Расчёт[править | править код]
Время расчёта и объём баз данных шахматных окончаний экспоненциально возрастают с количеством участвующих фигур. Размеры баз данных зависят как от количества фигур, так и от формата самой базы.
| Количество фигур | Количество позиций[5] | Размер таблиц |
|---|---|---|
| 2 | 462 | |
| 3 | 368 079 | 62,4 КБ |
| 4 | 125 246 598 | 29,5 МБ |
| 5 | 25 912 594 054 | 7,03 ГБ |
| 6 | 3 787 154 440 416 | 1,205 ТБ |
| 7 | 423 836 835 667 331 | 140 ТБ[a] 16,7 ТБ[b] |
| 8 | 38 176 306 877 748 245 | 10 ПБ[a]; 1,5 ПБ[b] |
К настоящему времени имеются базы данных для всех трёх-, четырёх-, пяти-, шести- и семифигурных окончаний (включая двух королей). Расчёт восьмифигурных окончаний проводится: просчитаны позиции без пешек[6] и позиции с двумя блокирующими друг друга пешками — белой и чёрной[7].
История[править | править код]
В истории компьютерных шахмат было несколько исследователей, высказывавших и реализовывавших идею игры компьютера в малофигурном окончании путём использования предварительно рассчитанной исчерпывающей таблицы всех возможных позиций.
В 1965 году Ричард Беллман (англ. Richard Bellman) впервые предложил использовать метод ретроспективного анализа для создания баз данных для решений шахматных и шашечных эндшпилей. В отличие от обычного прямого поиска, начинающегося с конкретной позиции, стоящей на доске, эндшпильные базы данных, включающие в себя все возможные расстановки фигур, проводят поиск в обратном направлении: начиная с позиций, где одна из сторон уже получила пат или мат, и заканчивая конкретной позицией, стоящей на доске, позволяя тем самым получить решение с абсолютной точностью. Таким образом, шахматному компьютеру во время игры больше не нужно производить расчёты эндшпиля, а достаточно лишь посмотреть в базе данных заранее посчитанный результат и сделать идеальный ход.
В 1970 году Томас Штрёляйн (нем. Thomas Ströhlein) защитил докторскую диссертацию, в которой анализировались такие окончания, как KQK, KRK, KPK, KQKR, KRKB и KRKN.
В 1977 году Кен Томпсон на конференции Международной федерации по обработке информации в Торонто представил построенную им таблицу для всех возможных положений в эндшпиле KRKQ «ладья и король против ферзя и короля». Общее число позиций для него составляет около 4 миллионов. Кен Томпсон провёл несколько показательных выступлений — компьютер играл за игрока, владеющего ладьёй. Этот эндшпиль теоретически проигрышный, шахматист уровня мастера, владея ферзём, обычно легко выигрывает его у любого противника. Поэтому компьютеру была поставлена задача максимально оттянуть свой теоретически неизбежный проигрыш. Результаты экспериментов, в которых компьютер играл с шахматистами, были довольно интересными. Против программы пытались играть экс-чемпион мира в игре по переписке Ханс Берлинер и чемпион Канады Лоуренс Дей. Ни тот, ни другой не смогли выиграть у программы, хотя любая позиция считалась выигрышной. Дело в том, что теоретически безупречная игра компьютера часто выглядела нелогично, противоречила принципам, предписываемым шахматной теорией (например, обычно рекомендуется не уводить ладью далеко от короля во избежание возможных вилок, но программа нередко делала это), необычные ходы компьютера сбивали шахматиста с толку, и он упускал выигрыш, не успевая за 50 ходов поставить мат или выиграть ладью.
В 1970-е и 1980-е годы идея предварительно рассчитанных эндшпилей развивалась очень медленными темпами, так как быстродействие и объём памяти тогдашних компьютеров были существенным ограничением и не позволяли получать подробные базы данных. Тем не менее, Кен Томпсон и другие энтузиасты продолжали медленно генерировать малофигурные окончания и, спустя некоторое время, были посчитаны все 4-фигурные окончания, а к концу 1980-х — уже все 5-фигурные окончания, включая такие интересные позиции, как KBBKN (Два слона против коня), KQPKQ (Ферзь и пешка против ферзя) и KRPKR (Ладья и пешка против ладьи). В 1995 году Льюис Стиллер (англ. Lewis Stiller) опубликовал работу, посвящённую исследованию некоторых 6-фигурных окончаний.
В 1998 году Евгений Налимов создал генератор шахматных окончаний, который оказался чрезвычайно эффективен. Благодаря новому эффективному генератору и росту производительности компьютеров к началу 2000-х посчитаны были все 6-фигурные окончания, что произвело настоящую революцию в понимании некоторых эндшпилей. Вскоре 6-фигурные окончания стали общедоступными в Интернете и являются таковыми по сей день.
В 2012 году были рассчитаны 7-фигурные таблицы для следующих материальных соотношений — четыре фигуры против трёх и пять фигур против двух. Расчёты проводились весной-летом 2012 года, авторы таблиц — Владимир Махнычев и Виктор Захаров, сотрудники ВМК МГУ. База данных названа «таблицами Ломоносова», так как они рассчитывались на суперкомпьютерах «Ломоносов» и IBM Blue Gene/P, установленных в Московском государственном университете имени М. В. Ломоносова. 7-фигурные таблицы окончаний впервые активно использовались при анализе партий Чемпионата Мира по шахматам 2012 года[8][9].
В 2018 году Боцзюнь Го сгенерировал 7-фигурные эндшпили в формате типа syzygy-tables, к ним открыт бесплатный онлайн-доступ[10][11].
В 2021 году Марк Бурзучки (англ. Marc Bourzutschky) посчитал 8-фигурные эндшпили без пешек, а также позиции с двумя блокирующими друг друга пешками — белой и чёрной[12].
См. также[править | править код]
Примечания[править | править код]
- ↑ Некоторые базы данных, например таблицы Налимова, содержат в себе оценки позиций при ходе только одной стороны — только белых или только чёрных. Одна и та же позиция при разной очереди хода содержится в разных таблицах.
- ↑ Таблицы Налимова имеют метрику DTM (англ. Depth to mate) — в выигранных позициях указывается количество ходов до мата.
- ↑ A260954 — OEIS. Дата обращения: 16 апреля 2019. Архивировано 16 апреля 2019 года.
- ↑ www.arves.org - 8-men Tablebase explorations “opposing 1 pawn” endgames. Дата обращения: 23 февраля 2022. Архивировано 2 февраля 2022 года.
- ↑ A318266 — OEIS. Дата обращения: 16 апреля 2019. Архивировано 16 апреля 2019 года.
- ↑ Восьмифигурки без пешек. (англ.). Дата обращения: 20 сентября 2021. Архивировано 4 августа 2021 года.
- ↑ Восьмифигурки с двумя взаимоблокирующими пешками. (англ.). Дата обращения: 20 сентября 2021. Архивировано 20 сентября 2021 года.
- ↑ Примеры анализа сложных ситуаций в семифигурных таблицах в блоге разработчиков 7TB, (ВМК МГУ). Дата обращения: 15 декабря 2012. Архивировано 4 октября 2013 года.
- ↑ Официальная публикация решающей партии матча на звание Чемпиона Мира по шахматам 2012 года Ананд — Гельфанд с комментариями ключевых моментов партии на основе таблиц Ломоносова Архивировано 2 июня 2012 года.
- ↑ KvK — Syzygy endgame tablebases. Дата обращения: 9 августа 2018. Архивировано 24 апреля 2022 года.
- ↑ "7-piece Syzygy tablebases are complete". lichess.org. Архивировано из оригинала 13 июля 2020. Дата обращения: 29 августа 2018.
- ↑ 8-piece endgame tablebases — first findings and interview! | ChessBase. Дата обращения: 24 ноября 2022. Архивировано 30 марта 2023 года.
Ссылки[править | править код]
- Syzygy endgame tablebases
- Endgame Database shredderchess.com
- On-line анализ вплоть до 6-фигурного эндшпиля.
- Lomonosov Endgame Tablebases (про 7-фигурные).
- A guide to Endgames Tablebase
- Эндшпильные таблицы Налимова.
- Мичи Д., Джонстон Р. Компьютер-творец / Пер. с англ.— М. Мир, 1987.— стр. 68, «Странный случай с таблицей Томпсона».
- Lomonosov Endgame Tablebases (англ.) // ChessOK.com