Векторная графика

Растровые изображения плохо масштабируются, при увеличении распадаются на пиксели, тогда как векторные изображения могут быть неограниченно увеличены без потери качества (примеры изображения были преобразованы в векторный формат SVG для показа на этом рисунке).
Ве́кторная гра́фика — способ представления графических объектов и изображений (формат описания) в компьютерной графике, основанный на математическом описании элементарных геометрических объектов, обычно называемых примитивами, таких как: точки, линии, сплайны, кривые Безье, круги, окружности, эллипсы, многоугольники.
Объекты векторной графики описываются совокупностью координат, параметров и атрибутов.
Термин «векторная графика» используется для подчёркивания отличий от растровой графики, в которой изображение представлено в виде графической матрицы, состоящей из пикселей.
При выводе на матричные устройства отображения (мониторы, механические устройства — принтеры, и пр.) векторная графика предварительно преобразуется в растровую графику, преобразование производится программно или аппаратно средствами современных видеокарт. Для плоттеров и векторных мониторов преобразование из векторного в растровый формат не требуется, так как в таких устройствах примитивы строятся перемещением пера или электронного луча.
Способ хранения изображения
[править | править код]Математически векторная графика основана на аналитической геометрии. В векторной графике примитивы описываются совокупностью координат опорных точек, параметрами примитива, к которым относятся например, исходные координаты, коэффициенты масштабирования, повороты, коэффициенты растяжения по осям. К атрибутам относят цвет и тип цветовой заливки областей, толщину и цвет линий.
В анимированной векторной графике при отображении на устройстве вывода координаты, атрибуты и параметры могут динамически изменяться во времени по заданным функциям от времени, создавая движущееся изображение.
Рассмотрим, к примеру, описание такого графического примитива, как окружность радиуса r. Для её построения необходимо задание следующих исходных данных:
- Координаты центра окружности.
- Значение радиуса.
- Цвет и/или текстура заливки (если окружность построена для отображения круга).
- Цвет и толщина линии контура в случае задания контура.
- Прозрачность заливки и контура.
- Порядок плана относительно других примитивов впереди, сзади (передний план, задний план). При отображении примитивы и объекты выводятся на устройство отображения последовательно и позднее выведенные объекты закрывают или накладываются на ранее выведенные объекты.
Координаты центра и радиус являются обязательными параметрами, остальные данные из описания окружности часто называют атрибутами и могут быть опущены. В этом случае при графическом выводе они заменяются атрибутами по умолчанию или текущими атрибутами.
Пример описания красного круга с координатами центра 79; 77, радиуса 20 с чёрным контуром толщиной 1 на языке XML (используемого в формате SVG, рекомендованном для применения в Википедии):
<circle cx="79" cy="77" r="20" fill="#f00" stroke="#000" stroke-width="1"/>
Преимущества векторного способа описания графики перед растровой графикой
[править | править код]- Объём данных, занимаемый описанием примитивов не зависит от реальной линейной величины описываемого объекта, что позволяет описать сколько угодно больших объектов файлом минимального размера. Например, для описания окружности произвольного радиуса требуется указание только 3 чисел, если исключить атрибуты.
- Так как информация об объекте хранится в числовой форме, можно бесконечно увеличивать изображение при выводе на устройство отображения, например, дуга окружности останется гладкой при любом увеличении. С другой стороны, если кривая описана в виде ломаной линии, состоящей из большого количества отрезков, то при невысоком увеличении она может выглядеть гладкой, однако при большом увеличении можно увидеть, что она на самом деле является ломаной.
- Описание объектов хранится в численном виде и может быть легко изменено. Поэтому перемещение, масштабирование, вращение, заливка и т. д. не ухудшает качества изображения. В графических векторных форматах обычно указывают размеры в аппаратно-независимых единицах (англ. device-independent unit), что позволяет улучшить качество изображения при растеризации для растровых устройств отображения.
Принципиальные недостатки векторной графики
[править | править код]Недостатками векторной графики являются[1]:
- Не каждое изображение может быть компактно описано в векторном виде — для высокого подобия к оригинальному изображению может потребоваться описание очень большого количества примитивов, что требовательно к объёму памяти, занимаемой изображением и на время необходимое для преобразования его в растровый формат для графического вывода на растровые устройства отображения.
- Перевод векторной графики в растровое изображение алгоритмически достаточно прост. Но обратное преобразование, как правило, сложно — это преобразование называют трассировкой растрового изображения и зачастую оно требует значительных вычислительных мощностей и процессорного времени, и не всегда обеспечивает высокое качество полученного векторного изображения.
- Спецификации векторных форматов (и, соответственно, рендереры векторной графики) намного сложнее таковых для растровой графики.
- Чтобы не иметь дело со сложными спецификациями, существуют «упрощённые» векторные форматы: например, в шрифте TrueType вместо линий толщины x — закрашенные фигуры. Или типографии требуют перевести текст в кривые. Перевод в такие форматы приводит к частичной или полной потере редактируемости.
- Преимущество векторной картинки — масштабируемость — пропадает, когда векторное изображение отображается в растре малого разрешения (например, в виде иконки 32×32 или 16×16). Чтобы не было «грязи», картинку под такие разрешения приходится редактировать вручную. В растеризаторах векторных шрифтов, например, TrueType применяются довольно сложные алгоритмы хинтинга, позволяющие при уменьшении избавиться от пропущенных (и, наоборот, излишне толстых) линий в изображениях символов.
Типичные примитивные объекты
[править | править код]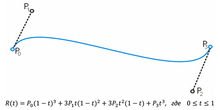
- Линии и ломаные линии.
- Многоугольники.
- Окружности и эллипсы.
- Кривые Безье.
- Безигон.
- Текст (в компьютерных шрифтах, таких как TrueType, изображение каждой буквы порождается по её математическому описанию в виде кривых Безье).
Этот список примитивов неполон. Есть разные типы кривых (Catmull-Rom сплайны, NURBS и т. д.), которые используются в различных приложениях. Также возможно рассматривать растровое изображение как примитивный объект, описанные как прямоугольник со сложной текстурой.
Векторные операции
[править | править код]
Векторные графические редакторы, типично, позволяют вращать, перемещать, отражать, растягивать, перекашивать, т. е. выполнять все аффинные преобразования над объектами, изменять порядок следования и комбинировать примитивы в составные объекты.
Также используются более изощрённые преобразования, например, булевы операции применённые к замкнутым фигурам как множествам точек, принадлежащих данным фигурам: объединение, дополнение, пересечение как показано на рисунке и т. д.
Векторная графика предпочтительна для простых или составных рисунков, которые должны быть аппаратно-независимыми или не нуждаются в фотореализме. К примеру, такие форматы как PostScript и PDF используют модель векторной графики.
Некоторые редакторы векторной графики
[править | править код]Некоторые форматы
[править | править код]- SVG — формат, рекомендуемый для использования в Википедии.
- EMF.
- CDR.
- CGM.
- DXF.
- OpenVG.
- GXL — редко используемый формат.
- WMF.
- EPS.
- PDF.
- AI.
- SWF — (Small Web Format; ранее расшифровывалось как Shockwave Flash, что вызывало путаницу с ShockWave) стандартное расширение для скомпилированных flash-файлов (анимации, игр и интерактивных приложений). SWF-файлы можно просматривать с помощью свободных плееров Gnash или swfdec. Для создания и работы с файлами SWF можно использовать свободный пакет программ командной строки SWFTools.
- DXE.
- FLA.
Примечания
[править | править код]- ↑ Andy Harris. Vector Graphics. wally.cs.iupui.edu. Дата обращения: 16 июня 2014. Архивировано из оригинала 18 мая 2012 года.
См. также
[править | править код]Ссылки
[править | править код]- Кариев Ч. А. , Масштабируемая векторная графика (Scalable Vector Graphics) Архивная копия от 13 августа 2010 на Wayback Machine (бесплатный курс), 07.11.2007
- Andy Harris. Vector Graphics. wally.cs.iupui.edu. Дата обращения: 16 июня 2014. Архивировано из оригинала 18 мая 2012 года.