Аналитическая геометрия
Аналити́ческая геоме́трия — раздел геометрии, в котором геометрические фигуры и их свойства исследуются средствами алгебры.
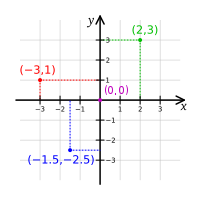
В основе этого метода лежит так называемый метод координат, впервые применённый Декартом в 1637 году. Каждому геометрическому соотношению этот метод ставит в соответствие некоторое уравнение, связывающее координаты фигуры или тела. Такой метод «алгебраизации» геометрических свойств доказал свою универсальность и плодотворно применяется во многих естественных науках и в технике[1]. В математике аналитическая геометрия является также основой для других разделов геометрии — например, дифференциальной, алгебраической, комбинаторной и вычислительной геометрии.
Историческая справка[править | править код]
Идея координат и уравнения кривой была не чужда ещё древним грекам. Архимед, и особенно Аполлоний Пергский, в своих сочинениях приводили так называемые симптомы конических сечений, которые в ряде случаев совпадают с нашими уравнениями. Однако дальнейшего развития эта идея тогда не получила по причине невысокого уровня древнегреческой алгебры и слабого интереса к кривым, отличным от прямой и окружности.
Потом в Европе использовал координатное изображение (для функции, зависящей от времени) Николай Орезмский (XIV век), который называл координаты, по аналогии с географическими, долготой и широтой. К этому времени развитое понятие о координатах уже существовало в астрономии и географии. Решающий шаг был сделан после того, как Виет (XVI век) сконструировал символический язык для записи уравнений и положил начало системной (символической) алгебре.
Около 1637 года Ферма распространил через Мерсенна мемуар «Введение в изучение плоских и телесных мест», где выписал (в символике Виета) уравнения различных кривых 2-го порядка в прямоугольных координатах. Для упрощения вида уравнений он широко использовал преобразование координат. Ферма наглядно показал, насколько новый подход проще и плодотворней чисто геометрического. Однако мемуар Ферма широкой известностью не пользовался. Гораздо большее влияние имела «Геометрия» Декарта[2][3], вышедшая в том же 1637 году, которая независимо и гораздо более полно развивала те же идеи.
Декарт включил в геометрию более широкий класс кривых, в том числе «механические» (трансцендентные, вроде спирали), и провозгласил, что у каждой кривой есть определяющее уравнение. Он построил такие уравнения для алгебраических кривых и провёл их классификацию (позже основательно переделанную Ньютоном). Декарт подчеркнул, хотя и не доказал, что основные характеристики кривой не зависят от выбора системы координат.
Система координат у Декарта была перевёрнута по сравнению с современной (ось ординат горизонтальна), и отрицательные координаты не рассматривались. Термины «абсцисса» и «ордината» изредка встречались у разных авторов, хотя в широкое употребление их ввёл только Лейбниц в конце XVII века, вместе с термином «координаты». Название «Аналитическая геометрия» утвердилось в самом конце XVIII века.
Декарт поместил в «Геометрию» множество примеров, иллюстрирующих огромную мощь нового метода, и получил немало результатов, неизвестных древним. Возможные пространственные применения он также упомянул, но эта идея не получила у него развития.
Аналитический метод Декарта немедленно взяли на вооружение ван Схоутен, Валлис и многие другие видные математики. Они комментировали и дополняли идеи «Геометрии», исправляли её недочёты, применяли новый метод в других задачах. Например, Валлис впервые рассмотрел конические сечения как плоские кривые (1655 год), причём, в отличие от Декарта, он уже использовал отрицательные абсциссы и косоугольные координаты.
Ньютон не только опирался на координатный метод в своих работах по анализу, но и продолжил геометрические исследования Декарта. Он классифицировал кривые 3-го порядка, выделив 4 типа и 58 видов; позже он добавил ещё 14. Эти результаты были получены около 1668 года, опубликованы вместе с его «Оптикой» в 1704 году. Система координат Ньютона уже ничем не отличается от современной. Для каждой кривой определяются диаметр, ось симметрии, вершины, центр, асимптоты, особые точки и т. п.
В своих «Началах» Ньютон старался всё доказывать в манере древних, без координат и бесконечно малых; однако несколько применений новых методов там всё же имеется. Гораздо бо́льшую роль аналитическая геометрия играет в его «Всеобщей арифметике», хотя там Ньютон в большинстве случаев не посчитал нужным привести доказательства, чем обеспечил работой на долгие годы целую армию комментаторов.
В первой половине XVIII века в основном продолжалось изучение алгебраических кривых высших порядков; Стирлинг обнаружил 4 новых типа, не замеченных Ньютоном. Были выявлены и классифицированы особые точки.
Клеро в 1729 году представил Парижской академии «Исследования о кривых двоякой кривизны». Эта книга по существу положила начало трем геометрическим дисциплинам: аналитической геометрии в пространстве, дифференциальной геометрии и начертательной геометрии.
Общую и очень содержательную теорию кривых и поверхностей (преимущественно алгебраических) предложил Эйлер. В своём «Введении в анализ бесконечно малых» (1748) он дал классификацию кривых 4-го порядка и показал, как определить радиус кривизны. Там, где это удобно, он использовал косоугольные или полярные координаты. Отдельная глава посвящена неалгебраическим кривым.
Во второй половине XVIII века аналитическая геометрия, получив мощную поддержку зрелого анализа, завоевала новые вершины (Лагранж, Монж), однако рассматривается уже скорее как аппарат дифференциальной геометрии.
Разделы[править | править код]
Основные разделы аналитической геометрии (согласно книге Н. В. Ефимова).
- Системы координат
- Элементы линейной алгебры
- Линейные операции над векторами
- Произведения векторов
- Матрицы и операции над ними
- Определители
- Обратная матрица и ранг матрицы
- Системы линейных алгебраических уравнений
- Кривые первого порядка
- Прямая на плоскости
- Прямая и плоскость в пространстве
- Кривые второго порядка
- Спираль
- Пространственные тела
- Поверхности второго порядка
- Цилиндр
- Сфера
- Конус
- Шар
См. также[править | править код]
Примечания[править | править код]
- ↑ Погорелов А. В., 1968, с. 7.
- ↑ Stillwell, John. Analytic Geometry // Mathematics and its History. — Second Edition. — Springer Science + Business Media Inc., 2004. — С. 105. — ISBN 0-387-95336-1.. — «the two founders of analytic geometry, Fermat and Descartes, were both strongly influenced by these developments.».
- ↑ Cooke, Roger. The Calculus // The History of Mathematics: A Brief Course (англ.). — Wiley-Interscience, 1997. — P. 326. — ISBN 0-471-18082-3.. — «The person who is popularly credited with being the discoverer of analytic geometry was the philosopher René Descartes (1596–1650), one of the most influential thinkers of the modern era.».
Литература[править | править код]
- Бортаковский А. С., Пантелеев А. В. Аналитическая геометрия в примерах и задачах: Учеб. пособие. — М.: Высш. шк., 2005. — 496 с. (Серия «Прикладная математика»).
- Веселов А. П., Троицкий Е. В. Лекции по аналитической геометрии. — СПб.: Лань, 2003. — 160 с.
- Делоне Б. Н., Райков Д. А. Аналитическая геометрия, в двух томах. — М., Л.: Гостехиздат, 1948, 1949.
- Ильин В. А., Позняк Э. Г. Аналитическая геометрия. — М.: ФИЗМАТЛИТ, 2002. — 240 с.
- История математики под редакцией А. П. Юшкевича в трёх томах.
- История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I.
- Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.
- Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
- Канатников А. Н., Крищенко А. П. Аналитическая геометрия. — М.: Издательство МГТУ им. Н. Э. Баумана, 2002. — 388 с. — ISBN 5-7038-1671-8.
- Мордухай-Болтовской Д. Д. Из прошлого аналитической геометрии // Труды института истории естествознании Акад. наук СССР, 1952, т. 4, с. 217—235.
- Погорелов А. В. Аналитическая геометрия. — 3-е изд.. — М.: Наука, 1968. — 176 с.
- Умнов А. Е. Аналитическая геометрия и линейная алгебра (pdf) — 544 с. ISBN 978-5-7417-0378-6 (на портале автора)