Граф Петерсена

Граф Петерсена
Назван в честь	Юлиус Петерсен
Вершин	10
Рёбер	15
Радиус	2
Диаметр	2
Обхват	5
Автоморфизмы	120 (S5)
Хроматическое число	3
Хроматический индекс	4
Род	1
Свойства	Кубический Сильно регулярный Дистанционно-транзитивный Снарк
Медиафайлы на Викискладе

Граф Петерсена — неориентированный граф с 10 вершинами и 15 рёбрами; достаточно простой граф, используемый в качестве примера и контрпримера для многих задач в теории графов.

Назван в честь Юлиуса Петерсена, построившего его в 1898 году как наименьший кубический граф без мостов, не имеющий рёберной раскраски в три цвета. При этом первое упоминание такого графа отмечено в статье Кемпе 1886 года, в которой отмечено, что его вершины можно рассматривать как десять прямых конфигурации Дезарга, а рёбра представляют пары прямых, пересечение которых не принадлежит конфигурации.

Дональд Кнут отмечает граф как примечательный тем, что даёт контрпримеры ко многим «оптимистичным» высказываниям о графах в целом.

Граф Петерсена появляется также в тропической геометрии: конус над графом Петерсена естественным образом идентифицируется модульным пространством пятиточечных рациональных тропических кривых.

Построение

Граф Петерсена как кнезеровский граф $KG_{5,2}$

Граф Петерсена является дополнением рёберного графа для $K_{5}$. Граф является также кнезеровским графом $KG_{5,2}$. Это означает, что граф имеет одну вершину для каждого 2-элементного подмножества 5-элементного множества, а две вершины связаны ребром тогда и только тогда, когда соответствующие 2-элементные подмножества не пересекаются. В качестве кнезеровского графа вида $KG_{2n-1,n-1}$ граф является нечётным графом.

Геометрически, граф Петерсена является графом, образованным вершинами и рёбрами полудодекаэдра, то есть додекаэдра с отождествлёнными противоположными вершинами, рёбрами и гранями.

Вложения

Граф Петерсена не является планарным. Любой непланарный граф имеет в качестве миноров либо полный граф $K_{5}$, либо полный двудольный граф $K_{3,3}$, но граф Петерсена имеет оба графа в качестве миноров. Минор $K_{5}$ можно получить путём стягивания рёбер совершенного паросочетания, например, пяти коротких рёбер на первом рисунке. Минор $K_{3,3}$ можно получить удалением одной вершины (например, центральной вершины 3-симметричного рисунка) и стягивания рёбер, инцидентных каждому соседу удалённой вершины.

Граф Петерсена имеет число пересечений 2 и является 1-планарным.

Общепринятый наиболее симметричный плоский рисунок графа Петерсена в виде пятиугольника внутри пятиугольника имеет пять пересечений. Однако это не самый оптимальный рисунок, минимизирующий число пересечений. Существует другой рисунок (показан справа) лишь с двумя пересечениями. Таким образом, граф Петерсена имеет число пересечений 2. Каждое ребро в этом рисунке пересекается не более одного раза, так что граф Петерсена является 1-планарным. На торе граф Петерсена может быть нарисован без пересечения рёбер. Таким образом, граф имеет ориентируемый род 1.

Граф Петерсена является графом единичных расстояний — его можно нарисовать на плоскости с рёбрами единичной длины.

Граф Петерсена может быть также нарисован (с пересечениями) на плоскости таким образом, что все рёбра имеют одинаковую длину. Таким образом, граф является графом единичных расстояний.

Простейшая неориентируемая поверхность, в которую граф Петерсена можно вложить без пересечений, — это проективная плоскость. Это вложение, которое задаётся построением графа Петерсена как полудодекаэдра. Вложение в проективную плоскость можно также образовать из стандартного пятиугольного рисунка графа Петерсена путём помещения плёнки (разрезанной бутылки Кляйна) внутрь пятиугольной звезды в центре рисунка и направления рёбер звезды через эту плёнку. Полученный рисунок имеет шесть пятиугольных граней. Это построение образует правильную карту и показывает, что граф Петерсена имеет неориентируемый род 1.

Симметрии

Граф Петерсена является сильно регулярным (с сигнатурой srg(10,3,0,1)). Граф является также симметричным, что означает, что он является рёберно-транзитивным и вершинно-транзитивным. Более строго, граф является 3-транзитивным по дугам — любой ориентированный путь из трёх путей в графе Петерсена может быть переведён в любой другой такой путь симметрией графа. Граф является одним из 13 кубических дистанционно-регулярных графов.

Группой автоморфизмов графа Петерсена является симметрическая группа $S_{5}$. Действие $S_{5}$ на граф Петерсена следует из его построения в виде кнезеровского графа. Любой гомеоморфизм графа Петерсена на себя, не отождествляющий смежные вершины, является автоморфизмом. Как показано на иллюстрациях, рисунки графа Петерсена могут показать симметрии в пяти направлениях или в трёх направлениях, но невозможно нарисовать граф Петерсена на плоскости таким образом, чтобы рисунок показывал полную симметрию группы графа.

Несмотря на высокую симметрию, граф Петерсена не является графом Кэли, он является наименьшим вершинно-транзитивным графом, не являющемся графом Кэли.

Гамильтоновы пути и циклы

Граф Петерсена является гипогамильтоновым — удаление любой вершины, как, например, центральной вершины на рисунке, делает граф гамильтоновым. Рисунок с тремя симметриями предложил Кемпе (Kempe 1886).

Граф Петерсена имеет гамильтонов путь, но не гамильтонов цикл. Граф является наименьшим кубическим графом без моста, не имеющим гамильтонова цикла. Граф является гипогамильтоновым, что означает, что хотя он не имеет гамильтонова цикла, удаление любой вершины делает его гамильтоновым, и это наименьший гипогамильтонов граф.

Как конечный связный вершинно-транзитивный граф, не имеющий гамильтонова цикла, граф Петерсена является контрпримером варианта гипотезы Ловаса, но каноническая формулировка гипотезы спрашивает о гамильтоновом пути и для графа Петерсена эта гипотеза выполняется.

Известны только пять связных вершинно-транзитивных графов без гамильтоновых циклов — полный граф K₂, граф Петерсена, граф Коксетера и два графа, полученных из графов Петерсена и Коксетера путём замены каждой вершины треугольником. Если G является 2-связным, r-регулярным графом с максимум 3r + 1 вершинами, то G является гамильтоновым или G является графом Петерсена.

Чтобы показать, что граф Петерсена не имеет гамильтонова цикла C, рассмотрим рёбра, соединяющие внутренний цикл из 5 вершин с внешним циклом. Если существует гамильтонов цикл, должно быть выбрано чётное число этих рёбер. Если выбрано только два ребра, их конечные вершины должны быть смежными в обоих циклах с 5 вершинами, что невозможно. Таким образом, должно быть выбрано 4 ребра. Предположим, что верхнее ребро не выбрано (все другие случаи аналогичны ввиду симметрии). Из 5 рёбер внешнего цикла два верхних ребра должны входить в гамильтонов цикл, так что два боковых ребра в цикл входить не должны, а тогда нижнее ребро должно входить в цикл. Два верхних ребра во внутреннем цикле должны быть выбраны, но тогда эти два ребра замыкают цикл, не являющийся полным, так что он не может быть частью гамильтонова цикла. Альтернативно, мы можем рассмотреть 3-регулярные графы с десятью вершинами, имеющими гамильтонов цикл, и показать, что ни один из этих графов не является графом Петерсена, путём нахождения цикла в каждом из них, более короткого, чем любой цикл графа Петерсена. Любой гамильтонов 3-регулярный граф с десятью вершинами состоит из цикла с десятью вершинами цикла C, плюс пять хорд. Если любая хорда соединяет две вершины вдоль C на расстоянии два или три друг от друга, то граф имеет 3-цикл или 4-цикл, а потому графом Петерсена быть не может. Если две хорды соединяют противоположные вершины цикла C на расстоянии четыре вдоль C, снова имеется 4-цикл. Остаётся только случай лестницы Мёбиуса, образованной соединением каждой пары противоположных сторон хордой, которая снова имеет 4-цикл. Поскольку обхват графа Петерсена равен пяти, он не может быть образован таким образом, а следовательно, не имеет гамильтонова цикла.

Раскраска

Раскраска рёбер графа Петерсена в 4 цвета

Раскраска вершин графа Петерсена в 3 цвета

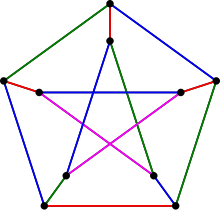
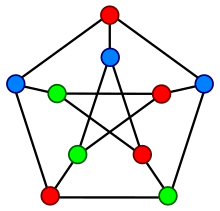
Граф Петерсена имеет хроматическое число 3, это означает, что вершины графа могут быть раскрашены в три цвета, но не в два, таким образом, что никакое ребро не соединяет две вершины одного цвета. Граф имеет предписанную раскраску в 3 цвета согласно теореме Брукса для предписанных раскрасок. Граф Петерсена имеет хроматический индекс 4, то есть раскраска рёбер требует четырёх цветов. Иными словами, граф не является суммой трех 1-факторов, что показал ещё сам Петерсен. Для доказательства этого требуется проверить четыре случая, чтобы показать, что не существует раскраски рёбер в 3 цвета. Как связный кубический граф без мостов с хроматическим индексом четыре, граф Петерсена является снарком. Этот граф — наименьший возможный снарк. Он был единственным известным снарком в период 1898—1946 годов. Теорема о снарках, высказанная в форме гипотезы Таттом (доказана в 2001 году Робертсоном, Сандерсом, Сеймуром и Томасом), утверждает, что любой снарк имеет граф Петерсена в качестве минора.

Кроме того, граф имеет дробный хроматический индекс 3, что подтверждает утверждение, что разница между хроматическим индексом и дробным хроматическим индексом может быть равна 1. Давняя гипотеза Голдберга—Сеймура предполагает, что это наибольшая возможная разница.

Число Туэ (вариант хроматического индекса) графа Петерсена равно 5.

Граф Петерсена требует по меньшей мере трёх цветов в любой (возможно, несобственной) раскраске, которая нарушает все симметрии. То есть характерное число раскраски графа равно трём. За исключением полных графов, есть только кнезеровский граф, характерное число которого не равно двум.

Другие свойства

Граф Петерсена:

• является 3-связным, а потому рёберно 3-связным и не имеющим мостов. См. Связный граф.
• имеет число независимости 4 и является 3-дольным. См. Задача о независимом множестве.
• является кубическим графом, имеет число доминирования 3, имеет совершенное паросочетание и 2-фактор.
• имеет 6 различных совершенных паросочетаний.
• является наименьшим кубическим графом с обхватом 5. (Это единственная $(3,5)$-клетка. Граф имеет только 10 вершин, поэтому он является единственным $(3,5)$-графом Мура.).
• имеет радиус 2 и диаметр 2. Это наибольший кубический граф с диаметром 2
• имеет спектр графа −2, −2, −2, −2, 1, 1, 1, 1, 1, 3.
• имеет 2000 остовных деревьев, больше чем любой кубический граф с 10 вершинами
• имеет хроматический многочлен $t(t-1)(t-2)\left(t^{7}-12t^{6}+67t^{5}-230t^{4}+529t^{3}-814t^{2}+775t-352\right).$
• имеет характеристический многочлен $(t-1)^{5}(t+2)^{4}(t-3)$, что делает его целым графом — графом, спектр которого полностью состоит из целых чисел.
• Между любыми двумя вершинами существует единственный путь длины не более двух.

Петерсеново семейство графов.

Гипотеза Петерсена о раскраске

Согласно Девосу, Нешетрилу и Распо «Цикл графа G — это множество C $\subseteq$ E(G), такое, что любая вершина графа (V(G),C) имеет чётную степень. Если G,H являются графами, мы определяем отображение φ: E(G) —> E(H) как непрерывное по циклам, если прообраз любого цикла в H является циклом в G. Франсуа Жагер (François Jaeger) сформулировал гипотезу, которая утверждает, что любой граф без мостов имеет непрерывное по циклам отображение в граф Петерсена. Жагер показал, что если гипотеза верна, то верна и гипотеза о двойном покрытии циклами длины 5 и гипотеза Бержа — Фалкерсона.».

Связанные графы

Обобщённый граф Петерсена G(n,k) образуется путём соединения вершин правильного n-угольника с соответствующими вершинами звёздчатого многоугольника с символом Шлефли {n/k}. Например, в этих обозначениях граф Петерсена граф имеет обозначение G(5,2) — его можно образовать соединением соответствующих вершин пятиугольника и пятиугольной звезды, при этом вершины звезды соединяются через одну. Обобщённые графы Петерсена также включает n-призмы G(n,1), граф Дюрера G(6,2), граф Мёбиуса — Кантора G(8,3), граф додекаэдра G(10,2), граф Дезарга G(10,3) и граф Науру G(12,5).

Петерсеново семейство графов состоит из семи графов, которые можно образовать из графа Петерсена путём нулевого и более числа применений преобразований Δ-Y или Y-Δ. Полный граф K₆ также входит в петерсеново семейство. Эти графы образуют запрещённые миноры для вложимых без зацеплений графов, графов, которые могут быть вложены в трёхмерное пространство таким образом, что никакие два цикла в графе не зацеплены

Граф Клебша состоит из копий графа Петерсена как порождённых подграфов — для каждой вершины v графа Клебша десять не являющихся соседями вершин v порождают копию графа Петерсена.

Ссылки

• Keller, Mitch. Kneser graphs Архивная копия от 5 мая 2018 на Wayback Machine PlanetMath
• Weisstein, Eric W. Petersen Graph (англ.) на сайте Wolfram MathWorld.
• Petersen Graph в Энциклопедии целочисленных последовательностей