Двенадцатеричная система счисления
Двенадцатеричная система счисления — позиционная система счисления с основанием 12. Используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. Существует другая система обозначения, где для недостающих цифр используют не A и B, а T (от англ. ten, десять) или D (от лат. decem, фр. dix, десять) или X (римское десять), а также E (от англ. eleven, одиннадцать) или O (от фр. onze, одиннадцать). Кроме того, на Западе иногда вместо A используют перевёрнутую двойку (![]() , U+218A ↊ turned digit two) и вместо B перевёрнутую тройку (
, U+218A ↊ turned digit two) и вместо B перевёрнутую тройку (![]() , U+218B ↋ turned digit three).
, U+218B ↋ turned digit three).
Число 12 могло бы быть очень удобным основанием системы счисления, так как оно делится нацело на 2, 3, 4 и 6, в то время как число 10 — основание десятичной системы счисления — делится нацело лишь на 2 и 5.
История
[править | править код]Двенадцатеричная система счисления сохранилась и в русском языке — для обозначения 12 предметов используется термин «дюжина», в XX веке многие предметы, в частности, столовые приборы, считали дюжинами. Посуда традиционно продаётся сервизами на 12 или 6 персон[1].
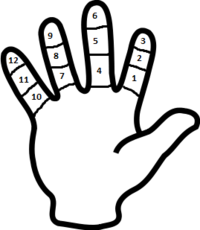
Происхождение двенадцатеричной системы счисления не вызывает сомнений — это пальцевой фаланговый счёт, при котором большим пальцем руки считают каждую фалангу четырёх пальцев той же руки[1].
Двенадцатеричный пальцевый счёт распространён на территории Индии, Индокитая, Пакистана, Афганистана, Ирана, Турции, Ирака, Сирии и Египта. Поэтому, предположительно, двенадцатеричная система счисления возникла в древнем Шумере, а позже использовалась в Ассирии и Вавилоне для деления дня и ночи на 12 равных частей (называемых danna), что удобно в силу совместимости двенадцатеричной системы счисления с шестидесятеричной (12 является делителем для 60). Также у них делили эклиптику на 12 beru по 30° каждая[2][3]. А в Древнем Египте светлое и тёмное время суток делили на 12 частей разной длительности[2].
В настоящее время двенадцатеричная система счисления используется жителями Тибета[4].
Некоторые народы Нигерии также используют двенадцатеричную систему счисления в настоящее время[источник не указан 1402 дня].
В Древнем Риме стандартной дробью была унция (лат. uncia) — 1⁄12 часть.
Двенадцатеричная система встречается в английской («имперской») системе мер, используемой до сих пор, 1 дюйм = 1⁄12 фута. Английские монеты также до 1968 года были основаны на ней: 12 пенни (пенсов) равнялись одному шиллингу[5].
В германских языках имеются отдельные числительные для обозначения 11 и 12, например, английские eleven (11) и twelve (12). Однако в прагерманском языке слова ainlif и twalif (буквально «один слева» и «два слева»), предполагают десятичный счёт[6][7].
Переход на двенадцатеричную систему счисления предлагался неоднократно. В XVIII веке её сторонником был знаменитый французский естествоиспытатель Бюффон. Во времена Великой Французской революции была учреждена «Революционная комиссия по весам и мерам», которая длительный период рассматривала подобный проект, однако усилиями Лагранжа и других противников реформы дело удалось свернуть. В 1944 году было организовано Американское двенадцатеричное общество (The Dozenal Society of America (DSA)), а в 1959 — Английское двенадцатеричное общество (The Dozenal Society of Great Britain (DSGB)), объединившие активных сторонников одноимённой системы счисления. Однако главным аргументом против этого всегда служили огромные затраты и неизбежная путаница при переходе[источник не указан 3246 дней].
Двенадцатеричный счёт
[править | править код]Элементом двенадцатеричной системы в современности может служить счёт дюжинами[8].
Первые три степени числа 12 имеют собственные названия[5]:
К удобствам двенадцатеричного счисления можно отнести большее (по сравнению с десятичной системой) количество делителей основания 12: 2, 3, 4, 6. На практике двенадцатеричная система (в смешанном виде) в настоящее время повсеместно распространена в часах[5].
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | 10 |
| 2 | 2 | 4 | 6 | 8 | A | 10 | 12 | 14 | 16 | 18 | 1A | 20 |
| 3 | 3 | 6 | 9 | 10 | 13 | 16 | 19 | 20 | 23 | 26 | 29 | 30 |
| 4 | 4 | 8 | 10 | 14 | 18 | 20 | 24 | 28 | 30 | 34 | 38 | 40 |
| 5 | 5 | A | 13 | 18 | 21 | 26 | 2B | 34 | 39 | 42 | 47 | 50 |
| 6 | 6 | 10 | 16 | 20 | 26 | 30 | 36 | 40 | 46 | 50 | 56 | 60 |
| 7 | 7 | 12 | 19 | 24 | 2B | 36 | 41 | 48 | 53 | 5A | 65 | 70 |
| 8 | 8 | 14 | 20 | 28 | 34 | 40 | 48 | 54 | 60 | 68 | 74 | 80 |
| 9 | 9 | 16 | 23 | 30 | 39 | 46 | 53 | 60 | 69 | 76 | 83 | 90 |
| A | A | 18 | 26 | 34 | 42 | 50 | 5A | 68 | 76 | 84 | 92 | A0 |
| B | B | 1A | 29 | 38 | 47 | 56 | 65 | 74 | 83 | 92 | A1 | B0 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | A0 | B0 | 100 |
Упоминание в фантастике
[править | править код]Двенадцатеричная система счисления упоминается и в фантастической литературе:
- применяется эльфами в книгах Джона Толкина;
- используется расой, заселившей Землю, после экспансии людей в галактику в романе Уолтера Миллера «Банк крови»;
- используется людьми будущего в романе Герберта Уэллса «Когда спящий проснётся», новелле Гарри Гаррисона «История конца» и рассказе Джеймса Блиша «Маникюр»;
- часто встречается в головоломках компьютерной игры Schizm 2 Chameleon;
- применяется в Мире Стержня в циклах книг Макса Фрая;
- в повести Джеральда Дэвида Нордли «Последняя инстанция» двенадцатеричной системой пользуется инопланетная раса ду’утианцев.
Примечания
[править | править код]- ↑ 1 2 Фомин, 1987, с. 8.
- ↑ 1 2 Macey S. L. The Dynamics of Progress : Time, Method, and Measure : [англ.] / Samuel L. Macey. — Atlanta, Georgia : University of Georgia Press[англ.], 1989. — P. 92. — 288 p. — ISBN 978-0-8203-3796-8. — ISBN 082033796X.
- ↑ Ifrah G. The Universal History of Numbers : From prehistory to the invention of the computer : [англ.] / Ифра, Джордж[англ.]. — John Wiley and Sons, 2000. — ISBN 0-471-39340-1.
- ↑ Nishikawa Y. ヒマラヤの満月と十二進法 : [] : [арх. 29 марта 2008] / Yoshiaki Nishikawa. — 2002. — [Пер. названия: Гималайская двенадцатеричная система и период полнолуния].
- ↑ 1 2 3 Фомин, 1987, с. 9.
- ↑ von Mengden F. The peculiarities of the Old English numeral system // Medieval English and its Heritage Structure : Meaning and Mechanisms of Change : [англ.] / Ferdinand von Mengden ; Eds.: Nikolaus Ritt, Herbert Schendl, Christiane Dalton-Puffer, Dieter Kastovsky. — Frankfurt : Peter Lang, 2006. — Vol. 16. — P. 125–145. — (Studies in English Medieval Language and Literature).
- ↑ von Mengden F. Cardinal Numerals : Old English from a Cross-Linguistic Perspective : [англ.] / Ferdinand von Mengden. — Berlin; New York : De Gruyter Mouton, 2010. — Vol. 67. — P. 159–161. — (Topics in English Linguistics).
- ↑ Фомин, 1987, с. 8–9.
Литература
[править | править код]- Фомин, С. В. § 3. Другие системы счисления и их происхождение // Системы счисления : [арх. 25 мая 2006]. — 5-е изд. — М. : Наука. Гл. ред. физ.-мат. лит., 1987. — С. 8–10. — 48 с. — (Попул. лекц. по мат. ; вып. 40). — 27 000 экз. — ББК 22.131. — УДК 511.2(021)(G).
- Ifrah G. From one to zero : A universal history of numbers : [англ.]. — New York : Viking Penguin, 1985. — xvi+503 p. — ISBN 0-14-009919-0.
Ссылки
[править | править код]- Whitten, N. A Comprehensive Dozenal Counting System : How to count in duodecimal – number names, scientific notation, prefixes, and abbreviations : Revised 10 March 2006 : [арх. 21 мая 2011] // Whitten Words : [англ.]. — 2004.
- Nature's Numbers : [англ.] : [арх. 13 апреля 2001] / Bill Lauritzen ; Buckminster Fuller Institute; Dozenal Society of America. — 1994.
В другом языковом разделе есть более полная статья Duodecimal (англ.). |