Соединение многогранников
Соединение многогранников — это фигура, составленная из некоторых многогранников, имеющих общий центр. Соединения являются трёхмерными аналогами многоугольных соединений, таких как гексаграмма.
Внешние вершины соединения можно соединить, образовав выпуклый многогранник, который называется выпуклой оболочкой. Соединение является огранкой выпуклой оболочки.
Внутри соединения образуется меньший выпуклый многогранник как общая часть всех членов соединения. Этот многогранник называется ядром для звёздчатых многогранников.
Правильные соединения[править | править код]
Правильные многогранные соединения можно определить как соединения, которые, как и в случае правильных многогранников, являются вершинно-транзитивными, рёберно транзитивными и гранетранзитивными. Существует пять правильных соединений многогранников.
| Соединение | Рисунок | Сферическое представление | Выпуклая оболочка | Ядро | Симметрия | Подгруппа для одной составляющей |
Двойственный |
|---|---|---|---|---|---|---|---|
| Два тетраэдра (звёздчатый октаэдр) |
 |

|
Куб | Октаэдр | *432 [4,3] Oh |
*332 [3,3] Td |
Самодвойственен |
| Пять тетраэдров |  |

|
Додекаэдр | Икосаэдр | 532 [5,3]+ I |
332 [3,3]+ T |
энантиоморфный хиральный двойник |
| Десять тетраэдров |  |

|
Додекаэдр | Икосаэдр | *532 [5,3] Ih |
332 [3,3] T |
Самодвойственен |
| Пять кубов |  |

|
Додекаэдр | Ромботриаконтаэдр | *532 [5,3] Ih |
3*2 [3,3] Th |
Пять октаэдров |
| Пять октаэдров |  |

|
Икосододекаэдр | Икосаэдр | *532 [5,3] Ih |
3*2 [3,3] Th |
Пять кубов |
Наиболее известно соединение двух тетраэдров. Кеплер назвал это соединение по-латински stella octangula (звёздчатый октаэдр). Вершины двух тетраэдров задают куб, а их пересечение является октаэдром, грани которого лежат на тех же плоскостях, что и грани составляющих тетраэдров. Таким образом, соединение является приведением к звезде октаэдра и, фактически, его единственным возможным приведением.
Звёздчатый октаэдр можно также рассматривать как двойственно-правильное соединение.
Соединение пяти тетраэдров имеет две зеркальные версии, которые вместе дают соединение десяти тетраэдров. Все соединения тетраэдров самодвойственны, а соединение пяти кубов двойственно соединению пяти октаэдров.
Двойственные соединения[править | править код]
Двойственное соединение — это соединение многогранника и двойственного ему, расположенных взаимно противоположно относительно общей вписанной или полувписанной сферы, так что ребро одного многогранника пересекает двойственное ребро двойственного многогранника. Существует пять таких соединений правильных многогранников.
| Компоненты | Рисунок | Выпуклая оболочка | Ядро | Симметрия |
|---|---|---|---|---|
| Два тетраэдра (звёздчатый октаэдр) |

|
Куб | Октаэдр | *432 [4,3] Oh |
| куб и октаэдр | 
|
Ромбододекаэдр | Кубооктаэдр | *432 [4,3] Oh |
| додекаэдр и икосаэдр |

|
Ромботриаконтаэдр | Икосододекаэдр | *532 [5,3] Ih |
| большой икосаэдр и большой звёздчатый додекаэдр |

|
Додекаэдр | Икосододекаэдр | *532 [5,3] Ih |
| малый звёздчатый додекаэдр и большой додекаэдр |

|
Икосаэдр | Додекаэдр | *532 [5,3] Ih |
Тетраэдр самодвойственен, так что двойственное соединение тетраэдра с двойственным ему является также звёздчатым октаэдром.
Двойственные соединения куб-октаэдр и додекаэдр-икосаэдр являются приведением к звезде кубооктаэдра и икосододекаэдра соответственно.
Соединение малого звёздчатого додекаэдра и большого додекаэдра выглядит внешне как тот же самый малый звёздчатый додекаэдр, поскольку большой додекаэдр содержится полностью внутри него. По этой причине изображение малого звёздчатого додекаэдра, приведённое выше, показано в виде рёберного каркаса.
Однородные соединения[править | править код]
В 1976 Джон Скиллинг (John Skilling) опубликовал статью Однородные соединения однородных многогранников [1], в которой перечислил 75 соединений (включая 6 бесконечных множеств призматических соединений, №20-25), полученных из однородных многогранников с помощью вращений. (Каждая вершина является вершинно транзитивной.) Список включает пять соединений правильных многогранников из списка выше. [1]
Эти 75 однородных соединений приведены в таблице ниже. В большинстве соединений разные цвета соответствуют разным составляющим. Некоторые хиральные пары раскрашены согласно зеркальной симметрии.
- 1—19: Смесь (4,5,6,9,17 являются пятью правильными соединениями)

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
- 20—25: Симметрия призм, вложенная в диэдральную симметрию в трёхмерном пространстве,

|

|

|

|

|

|
- 26—45: Симметрия призм, вложенная в октаэдральную или икосаэдральную симметрию,

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
- 46—67: Тетраэдральная симметрия, вложенная в октаэдральную или икосаэдральную симметрию,

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
- 68—75: энантиоморфные пары

|

|

|

|

|

|

|

|
Другие соединения[править | править код]
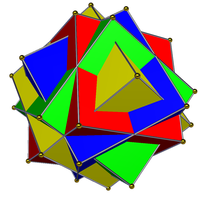
|
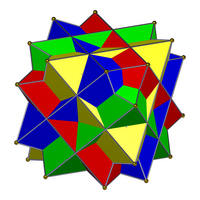
|
| Соединение четырёх кубов (слева) не является ни правильным, ни двойственным, ни однородным соединением. Двойственное ему соединение четырёх октаэдров (справа) — однородное. | |
- Соединение трёх октаэдров
- Соединение четырёх кубов
Два многогранника, являющиеся соединениями, но их элементы строго заключены в малый сложный икосододекаэдр (соединение икосаэдра и большого додекаэдра) и большой сложный икосододекаэдр (соединение малого звёздного додекаэдра и большого икосаэдра). Если принять обобщённое определение однородного многогранника, они будут однородными.
Секция энтианоморфных пар в списке Скиллинга не содержит соединения двух больших плосконосых додекоикосододекаэдров, поскольку грани-пентаграммы совпадают. Удаление совпадающих граней приведёт к соединению двадцати октаэдров.
Четырёхмерные соединения[править | править код]

|

|
| 75 {4,3,3} | 75 {3,3,4} |
|---|
В четырёхмерном пространстве существует большое число правильных соединений правильных многогранников. Коксетер перечислил некоторые из них в своей книге Правильные многогранники [2].
Самодвойственные:
| Соединение | Симметрия |
|---|---|
| 120 пятиячейников | [5,3,3], порядок 14400 |
| 5 двадцатичетырёхячейников | [5,3,3], порядок 14400 |
Двойственные пары:
| Соединение 1 | Соединение 2 | Симметрия |
|---|---|---|
| 3 шестнадцатиячейника[3] | 3 тессеракта | [3,4,3], порядок 1152 |
| 15 шестнадцатиячейников | 15 тессерактов | [5,3,3], порядок 14400 |
| 75 шестнадцатиячейников | 75 тессерактов | [5,3,3], порядок 14400 |
| 300 шестнадцатиячейников | 300 тессерактов | [5,3,3]+, порядок 7200 |
| 600 шестнадцатиячейников | 600 тессерактов | [5,3,3], порядок 14400 |
| 25 двадцатичетырёхячейников | 25 двадцатичетырёхячейников | [5,3,3], порядок 14400 |
Однородные соединения с выпуклыми четырёхмерными многогранниками:
| Соединение 1 вершинно транзитивное |
Соединение 2 ячейно транзитивное |
Симметрия |
|---|---|---|
| 2 шестнадцатиячейника[4] | 2 тессеракта | [4,3,3], порядок 384 |
| 100 двадцатичетырёхячейников | 100 двадцатичетырёхячейников | [5,3,3]+, порядок 7200 |
| 200 двадцатичетырёхячейников | 200 двадцатичетырёхячейников | [5,3,3], порядок 14400 |
| 5 шестисотячейников | 5 стодвадцатиячейников | [5,3,3]+, порядок 7200 |
| 10 шестисотячейников | 10 стодвадцатиячейников | [5,3,3], порядок 14400 |
Двойственные позиции:
| Соединение | Симметрия |
|---|---|
| 2 пятиячейника {{3,3,3}} |
[[3,3,3]], порядок 240 |
| 2 двадцатичетырёхячейника[5] {{3,4,3}} |
[[3,4,3]], порядок 2304 |
Соединение правильных звёздных четырёхмерных многогранников[править | править код]
Самодвойственные звёздные соединения:
| Соединение | Симметрия |
|---|---|
| 5 {5,5/2,5} | [5,3,3]+, порядок 7200 |
| 10 {5,5/2,5} | [5,3,3], порядок 14400 |
| 5 {5/2,5,5/2} | [5,3,3]+, порядок 7200 |
| 10 {5/2,5,5/2} | [5,3,3], порядок 14400 |
Двойственные пары соединений звёзд:
| Соединение 1 | Соединение 2 | Симметрия |
|---|---|---|
| 5 {3,5,5/2} | 5 {5/2,5,3} | [5,3,3]+, порядок 7200 |
| 10 {3,5,5/2} | 10 {5/2,5,3} | [5,3,3], порядок 14400 |
| 5 {5,5/2,3} | 5 {3,5/2,5} | [5,3,3]+, порядок 7200 |
| 10 {5,5/2,3} | 10 {3,5/2,5} | [5,3,3], порядок 14400 |
| 5 {5/2,3,5} | 5 {5,3,5/2} | [5,3,3]+, порядок 7200 |
| 10 {5/2,3,5} | 10 {5,3,5/2} | [5,3,3], порядок 14400 |
Однородные соединения звёзд:
| Соединение 1 вершинно транзитивное |
Соединение 2 ячейно транзитивное |
Симметрия |
|---|---|---|
| 5 {3,3,5/2} | 5 {5/2,3,3} | [5,3,3]+, порядок 7200 |
| 10 {3,3,5/2} | 10 {5/2,3,3} | [5,3,3], порядок 14400 |
Теория групп[править | править код]
В терминах теории групп, если G является группой симметрии соединения многогранников и группа действует транзитивно на многогранник (так что любой многогранник может быть в любой другой, как в однородных соединениях), тогда, если H является стабилизатором одного выбранного многогранника, многогранники могут быть определены по орбите G/H.
Соединение мозаик[править | править код]
Существует восемнадцать двупараметрических семейств правильных соединений мозаик на евклидовой плоскости. В гиперболическом пространстве известны пять однопараметрических семейств и семнадцать изолированных мозаик, но список не является завершённым.
Евклидовы и гиперболические семейства 2 {p,p} (4 ≤ p ≤ ∞, p целое) аналогичны сферическим звёздчатым октаэдрам, 2 {3,3}.
| Самодвойственные | Двойственные | Самодвойственные | |
|---|---|---|---|
| 2 {4,4} | 2 {6,3} | 2 {3,6} | 2 {∞,∞} |

|

|

|

|
| 3 {6,3} | 3 {3,6} | 3 {∞,∞} | |

|

|

| |
Известным семейством правильных еквлидовых соединений сот в пространствах размерности пять и выше является бесконечное семейство гиперболических сот, имеющих общие вершины и грани. Такое соединение может иметь произвольное число ячеек в соединении.
Существуют также двойственно-правильные соединения мозаик. Простым примером служит E2-соединение шестиугольной мозаики и её двойственной треугольной. Евклидово соединение двух гиперболических сот правильно и двойственно правильно.
Примечания[править | править код]
- ↑ Skilling, 1976, с. 447–457.
- ↑ Coxeter, 1973, с. 305, Таблица VII.
- ↑ Richard Klitzing, Uniform compound Звёздчатый икосаэдр Архивная копия от 4 марта 2016 на Wayback Machine
- ↑ Richard Klitzing, Uniform compound Demidistesseract Архивная копия от 4 марта 2016 на Wayback Machine
- ↑ Richard Klitzing, Uniform compound Dual positioned 24-cells Архивная копия от 2 апреля 2016 на Wayback Machine
Литература[править | править код]
- John Skilling. Uniform Compounds of Uniform Polyhedra // Mathematical Proceedings of the Cambridge Philosophical Society. — 1976. — Т. 79. — doi:10.1017/S0305004100052440..
- P. Cromwell. Polyhedra. — United Kingdom: Cambridge, 1997. — С. 79–86 Archimedean solids. — ISBN 0-521-55432-2.
- Magnus Wenninger. Dual Models. — Cambridge: Cambridge University Press, 1983. — P. 51–53..
- Michael G. Harman. Polyhedral Compounds. — unpublished manuscript, 1974..
- Edmund Hess. Zugleich Gleicheckigen und Gleichflächigen Polyeder. — Schriften der Gesellschaft zur Berörderung der Gasammten Naturwissenschaften zu Marburg. — 1876. — Т. 11. — С. 5–97.
- H.S.M Coxeter. Chapter 8: Truncation // Regular Polytopes. — 3rd edition. — New York: Dover Publications Inc., 1973. — ISBN 0-486-61480-8.
- Anthony Pugh. Polyhedra: A visual approach. — California: University of California Press Berkeley, 1976. — ISBN 0-520-03056-7. стр. 87 Five regular compounds
Внешние ссылки[править | править код]
- MathWorld: Polyhedron Compound
- Compound polyhedra – from Virtual Reality Polyhedra
- Skilling's 75 Uniform Compounds of Uniform Polyhedra
- Skilling's Uniform Compounds of Uniform Polyhedra
- Polyhedral Compounds
- http://users.skynet.be/polyhedra.fleurent/Compounds_2/Compounds_2.htm
- Compound of Small Stellated Dodecahedron and Great Dodecahedron {5/2,5}+{5,5/2}
Для улучшения этой статьи желательно:
|